Тема: «Организация движения поездов повышенной массы и длины на железнодорожных участках» Выпускная квалификационная работа (стр. 2 )

Рис. 1. Зависимость мощности локомотива от скорости движения

Определив из формулы (1.2) величину силы тяги

  (1.2)

  (1.3)

Из равенства (4.31) следует, что независимо от вида тяги при заданных технических средствах и принятом типе локомотива увеличение массы поезда на рабочей части профиля пути возможно только за счет снижения уровня скорости в интервале от конструкционной до расчетной и, наоборот, увеличить скорость можно, уменьшая массу поезда.

Поскольку равенство (1.3) выведено из условия равномерности скорости на расчетном подъеме в период, когда сила тяги уравновешивается силами сопротивления, то сделанные выводы справедливы и для любых других рабочих элементов профиля в периоды, когда сила тяги уравновешивается силами сопротивления. Так как масса поезда, рассчитанная по величине расчетного подъема на перегоне (участке), остается постоянной, то при переходе поезда с расчетного подъема на более легкие скорость возрастает, стремясь к равновесному значению, а затем снижается при переходе поезда на более трудные участки профиля.

На нерабочей части профиля скорость движения и масса поезда не взаимосвязаны. Здесь скорость ограничивается техническим состоянием вагонов, локомотивов, железнодорожного пути, включая искусственные сооружения, а также условиями торможения поездов. В каждом конкретном случае принимается меньшее значение скорости из перечисленных ограничений.

Ходовая скорость Vх, км/ч, на участке длиной L определяется средними уровнями скорости V на рабочей части профиля пути и Vн на нерабочей его части, а также соотношением доли  протяженности рабочей части профиля, и доли  ( 1 ) нерабочей части

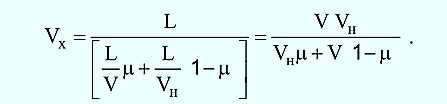
В знаменателе уравнения (в квадратных скобках) первое слагаемое представляет время хода по рабочей части профиля участка, а второе – по его нерабочей части.

Протяженность нерабочей части профиля в общей длине участка зависит от многих факторов и прежде всего от мощности локомотива, при ляет величину средней скорости на рабочей части профиля, а также от уровня максимальной скорости, установленной по техническому состоянию подвижного состава и железнодорожного пути.

Чем меньше удельная мощность локомотива и, следовательно, ниже средняя скорость движения на рабочей части профиля пути и чем выше уровень максимальной скорости, тем меньше будет доля нерабочей части профиля пути. В этом случае большую часть профиля поезд будет проходить с тягой.

Исследования показывают, что при средней скорости движения на рабочей части профиля (60–70) км/ч и максимальной – 90 км/ч, в зависимости от характера профиля доля рабочей части профиля пути сохраняется в пределах 80–90 %. На одних и тех же участках доля  для тепловозной тяги выше, чем для электрической. Объясняется это тем, что тепловозы имеют меньшую удельную мощность и реализуют более низкие скорости при выходе поезда на спуски. В результате поезд, управляемый тепловозом, двигается по спуску с тягой до момента достижения максимальной скорости, преодолевая большее расстояние, чем электровоз. Чем больше мощность локомотива, приходящаяся на 1 т массы поезда, тем выше ходовая скорость и тем большее расстояние поезд проходит с использованием режимов выбега или торможения. Удельный же вес скорости движения на нерабочей части профиля (от уровня ходовой) для вышеуказанного значения м составляет всего 5–8 %, остальные 92–95 % приходятся на рабочую часть, где скорость определяется в основном величинами массы поезда и мощности локомотива.

Необходимо отметить, что на долю нерабочей части профиля пути заметное влияние оказывает постоянно действующее ограничение скорости как по станциям, так и по перегонам. Современные (мощные) тепловозы и электровозы обладают достаточно большой удельной мощностью, в результате чего скорость на рабочей части профиля приближается к максимально допускаемой, а в местах постоянно действующих предупреждений и ограничений превышает ее. Это приводит к частым торможениям и, как следствие, к потерям топлива  и электроэнергии на тягу поездов. Устранить эти потери можно только за счет повышения допускаемых скоростей и ликвидации ограничений скорости как по станциям, так и по перегонам.

Аналитическая взаимосвязь между скоростью движения поезда и его массой в целом на участке определяется вторым законом Ньютона, который устанавливает, что ускорение тела, м/с 2, в результате действия на него силы F пропорционально величине этой силы и обратно пропорционально массе тела M

(1.5)

Если ускорение, сила и масса измеряются в системе СИ, то коэффициент  равен единице, т. е. величина этого коэффициента зависит от используемой в расчетах системы измерения единиц.

Согласно формуле (1.5) сила, равная 1 Н, воздействуя на тело массой 1 кг, сообщает ему ускорение 1 м/с 2.

В эксплуатационных расчетах для всех поездов его величину принимают в среднем 0,06.

В уравнении (1.6), называемом уравнением движения поезда, подразумевается, что в режиме торможения сила тяги Fk=0 , и наоборот, в режиме тяги – сила торможения B=0 . Поскольку в этом уравнении все величины измеряются в системе СИ, то коэффициент=1.

В эксплуатационной работе железных дорог, а также в разнообразных инженерных расчетах в большинстве случаев используется внесистемная единица измерения скорости – км/ч, в отличие от м/с в системе СИ. В связи с этим прирост скорости в единицу времени, т. е. ускорение dV/ dt, определяемое по формуле (1.7), целесообразно измерять в километрах на час в квадрате (км/ч2 )

В целях перевода ускорения в эту единицу измерения, а также перехода от полных значений сил к удельным, умножим числитель и знаменатель уравнения движения поезда на g (ускорение силы тяжести). Тогда в знаменателе произведение g(Q+ Mл) будет представлять вес поезда в кН, а отношения сил

Fk, Wk и В к весу поезда определит соответствующие удельные силы – fk wk, b. Одновременно приняв ускорение силы тяжести равным

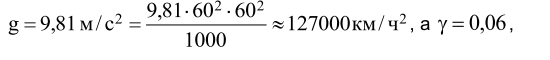получим

т. е.

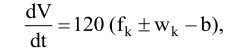
где 120  – ускорение поезда при воздействии силы в 1Н/кН, км/ч2; – результирующая удельная сила, воздействующая на поезд, Н/кН.

Из уравнения (1.7) следует, что если на поезд будет воздействовать постоянная удельная сила, равная 1 Н/кН, то скорость поезда возрастет на 120 км/ч за час действия силы.

Поэтому скорость движения на рабочей части профиля пути при заданном профиле участка и серии локомотива возможно изменять только за счет массы поезда. Однако так как средняя ходовая скорость движения на участке зависит также еще от максимально допустимого уровня скорости и ее ограничений по состоянию пути и искусственных сооружений, то прирост массы, измеряемый в процентах, всегда бывает больше, чем связанное с этим уменьшение скорости хода по участку, т. е. если масса поезда, предположим, увеличена на 20 %, то средняя скорость снизится в меньшей мере.

Наоборот, если попытаться повысить среднюю ходовую скорость на несколько процентов, то для этого необходимо уменьшить массу поезда, но в большей степени, чем повышается скорость.

Это обстоятельство необходимо всегда учитывать, когда решается вопрос о целесообразности повышения массы поезда, или скорости, при заданном типе локомотива.

Поэтому скорость движения на рабочей части профиля пути при заданном профиле участка и серии локомотива возможно изменять только за счет массы поезда. Однако так как средняя ходовая скорость движения на участке зависит также еще от максимально допустимого уровня скорости и ее ограничений по состоянию пути и искусственных сооружений, то прирост массы, измеряемый в процентах, всегда бывает больше, чем связанное с этим уменьшение скорости хода по участку, т. е. если масса поезда, предположим, увеличена на 20 %, то средняя скорость снизится в меньшей мере.

Наоборот, если попытаться повысить среднюю ходовую скорость на несколько процентов, то для этого необходимо уменьшить массу поезда, но в большей степени, чем повышается скорость.

Это обстоятельство необходимо всегда учитывать, когда решается вопрос о целесообразности повышения массы поезда, или скорости, при заданном типе локомотива.

Формулами (1.9), (2.0) и (2.1) можно пользоваться в аналитических расчетах определения скорости, времени и расстояния только в тех случаях, когда результирующая сил, действующих на поезд, постоянна на рассматриваемом отрезке пути. В связи с тем, что сила тяги локомотива и силы сопротивления движению поезда изменяются в зависимости от скорости движения и характера профиля пути, задача определения скорости и времени хода решается интегрированием уравнения движения поезда. В этих целях могут быть использованы аналитические и графические способы интегрирования уравнения, требующие значительных затрат рабочего времени.

В экономической оценке различных вариантов норм массы и ходовой скорости движения поездов используется участковая скорость, во многом зависящая от уровня ходовой. На основе участковой скорости определяется время оборота вагонов и локомотивов, их рабочий и эксплуатируемый парк, количество локомотивных бригад, а также связанные с ними денежные затраты. Участковая скорость рассчитывается отдельно для каждого железнодорожного участка, а затем определяется ее средневзвешенное значение для рассматриваемого железнодорожного полигона. Ее расчет может быть выполнен с использованием аналитических зависимостей или более точно по графикам движения поездов.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11