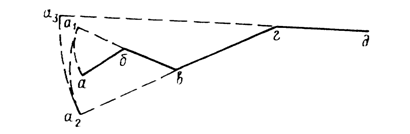
Рис. 11
Измерение ломаных отрезков производят по частям или путем их последовательного спрямления (способ наращивания). При этом способе (рис. 11) устанавливают ножки измерителя в точках а и б, совмещают край линейки с направлением б–в, вращают измеритель вокруг ножки в точке б и устанавливают вторую ножку измерителя у края линейки в точке а1, т. е. на продолжении отрезка бв. После этого перемещают ножку циркуля из точки б в точку в и получают сумму отрезков аб и бв. Действуя аналогично, получают в растворе циркуля а3д общую длину ломаной линии абвгд.
Для контроля измерения проводят в обратном направлении, от точки д к точке а.
Для измерения криволинейных отрезков применяются специальные приборы – курвиметр, циркуль-измеритель с постоянным раствором, а также существует способ наращивания.
Курвиметр состоит из колесика, связанного со стрелкой, которая указывает на циферблате длину линии в сантиметрах. Удерживая курвиметр перпендикулярно к плоскости карты, ведут его колесико по измеряемому отрезку.
Перед применением курвиметра необходимо определить цену его деления. Для этого выбирают отрезок известной длины и устанавливают, какое число делений курвиметра п будет соответствовать этому отрезку. Тогда цена деления курвиметра
![]() .
.
Перед началом измерения отсчет на циферблате курвиметра выводят на 0.
Применение циркуля-измерителя с постоянным раствором сводится к измерению малых хорд. Берут раствор циркуля порядка двух-пяти миллиметров и определяют по отрезку с известной длиной dизв длину отрезка, взятого в раствор циркуля:
![]() ,
,
где п – число перестановок циркуля. После определения dраст измеряют длину криволинейного отрезка. Для измерений следует пользоваться циркулем с регулирующим винтом, dраст следует брать меньше при большей извилистости измеряемой линии.
Применение способа наращивания при измерении криволинейных отрезков такое же, как и при измерении ломаных отрезков (измеряют малые хорды, на которые делится криволинейный отрезок).
Практика измерений криволинейных отрезков показывает, что наиболее точным является применение циркуля-измерителя с постоянным раствором.
Практическая часть
Сопоставьте точность измерения прямолинейного отрезка тремя способами: по масштабной линейке, циркулем-измерителем с постоянным раствором, с помощью курвиметра.
Перед измерениями, пользуясь графиком линейного масштаба учебной карты, определите цену деления курвиметра ск и длину отрезка, взятого в раствор циркуля, dраст.
Измерьте на карте ломаную линию (длину контура: участка, относящегося к населенному пункту) двумя способами: по частям с помощью масштабной линейки и способом наращивания.
Измерьте с помощью курвиметра два криволинейных отрезка: участок реки между сторонами километровой сетки (длина 12 – 14 см) и участок проселочной дороги.
6. ИЗМЕРЕНИЕ ПЛОЩАДЕЙ
Границы участков, площади которых необходимо определить на плане или карте, могут иметь прямолинейное или произвольное очертание.
При прямолинейных очертаниях определение площади возможно двумя способами: графическим (по расчетным формулам конкретных геометрических фигур) и аналитическим (по координатам вершин углов многоугольника).
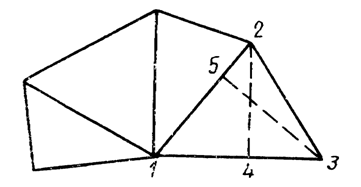
Рис. 12
В первом случае участок разбивают преимущественно на треугольники, реже на прямоугольники и трапеции (рис. 12). Измеряют линейные элементы (стороны, высоты) и по формулам геометрии вычисляют площади каждой фигуры. Для контроля площади вычисляют дважды, меняя измеряемые элементы. Например, в треугольнике 1–2–3 в одном случае измеряют основание 1–2 и высоту 3–5, в другом – основание 1–3 и высоту 2–4. Расхождение между двумя значениями площадей не должно превосходить ![]() [га], где m – знаменатель численного масштаба. Точность определения площадей примерно
[га], где m – знаменатель численного масштаба. Точность определения площадей примерно ![]() измеряемой величины.
измеряемой величины.
Вычисление площади аналитическим способом, по координатам вершин углов многоугольника, обеспечивает более высокую точность (до ![]() измеряемой величины).
измеряемой величины).
Расчетная формула для определения площади многоугольника (в простейшем случае треугольника – рис. 13):
![]()
![]() .
.
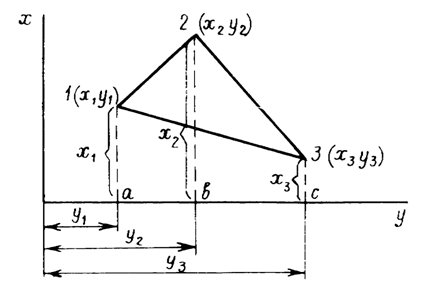
Рис. 13
Произведя соответствующие алгебраические действия и преобразования, получим расчетные формулы:
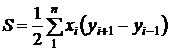 ;
;
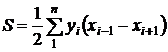 ,
,
где i = 1, 2, 3 ... – номера вершин полигона; ![]() – номер последующей вершины;
– номер последующей вершины; ![]() – номер предыдущей вершины.
– номер предыдущей вершины.
При произвольных очертаниях границ участков определение площади возможно также двумя способами: графическим (палетки) и механическим (планиметры).
Для определения площадей небольших участков с криволинейными контурами применяют палетки – квадратные (рис. 14) и параллельные (рис. 15).

Рис. 14 | Рис. 15 |
Палетки изготавливают на прозрачном материале, расстояние между линиями 1–2 мм. Квадратная палетка применяется для малых участков, имеющих площадь на плане до 2 см2. Подсчитывают число полных клеток, доли неполных клеток учитывают на глаз. Точность измерения примерно ![]() .
.
Параллельную палетку применяют для участков, площадь которых на плане до 10 см2. Палетку на измеряемый контур накладывают так, чтобы точки 1 и 2 расположились между параллельными линиями. Тогда отрезки 3–4, 5–6 и так далее можно считать полусуммой оснований соответствующих трапеций. Найдя суммарную длину этих отрезков и умножив ее на высоту трапеции (т. е. на величину расстояния между параллельными линиями), получим площадь контура.
При механическом способе применяют планиметры различных конструкций, чаще всего – полярный планиметр.
6.1. Устройство и поверки планиметра
Полярный планиметр (рис. 16) состоит из трех частей: полюсного 1 и обводного 2 рычагов и каретки счетного механизма. Полюсный рычаг с одной стороны имеет груз с иглой 3, которая является полюсом планиметра; перед началом измерений иглу вдавливают в бумагу. С другой стороны полюсный рычаг заканчивается шарниром 6, с помощью которого он соединяется с кареткой счетного механизма. На конце обводного рычага имеется обводный шпиль 7, которым обводят контур участка, удерживая рычаг за ручку 8. Для того чтобы шпиль не царапал карту, существует штифт 9, длину которого можно регулировать с помощью гайки. В более поздней конструкции планиметра шпиль заменен увеличительным стеклом с точкой в центре. На обводном рычаге расположена каретка со счетным механизмом (рис. 17). Он состоит из счетного колеса 12, счетчика целых оборотов счетного колеса 13 и верньера 14. При измерении площади участка ободок счетного колеса 15 и ролик 16 должны находиться в пределах листа карты.
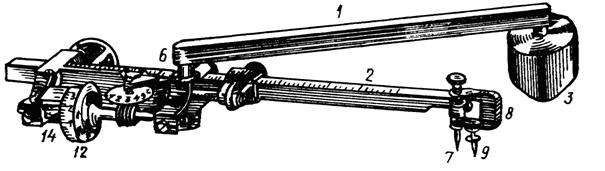
Рис. 16
Счетное колесо разделено на 100 делений, каждые 10 делений оцифрованы. Десятые доли делений счетного колеса определяются по верньеру. Делением планиметра называется одна тысячная часть окружности счетного колеса.
Отсчет по планиметру всегда состоит из четырех цифр. Первая цифра – ближайшая к указателю меньшая цифра счетчика оборотов 13, вторая и третья цифры – сотни и десятки делений на счетном колесе, предшествующих указателю верньера 14 (начальному штриху шкалы верньера, т. е. 0); четвертая цифра – номер штриха верньера, совпадающего с каким-либо штрихом счетного колеса (единицы делений). На рис. 17 отсчет по счетному механизму составляет 3578.
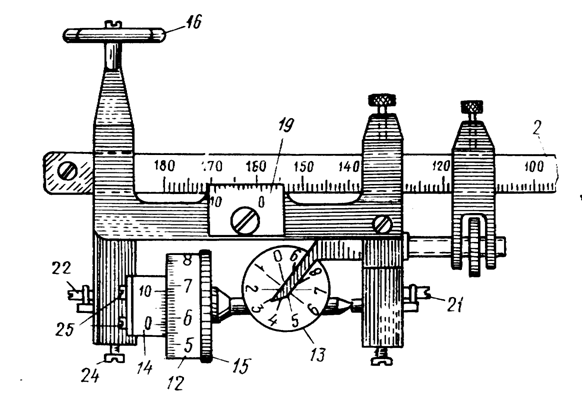
Рис. 17
Прежде чем приступать к измерению площади, необходимо убедиться в исправности планиметра. Он должен удовлетворять двум условиям.
1. Счетное колесо должно вращаться свободно и без колебаний. Если ось колеса слишком зажата в удерживающих ее центрах или колесо касается примыкающего к нему верньера, то вращение его будет задерживаться и могут возникнуть ошибки при измерениях.
Поверка выполняется путем вращения счетного колеса рукой. Оно должно вращаться по инерции 3–5 с. Между краем счетного колеса и верньером должен быть зазор не более толщины листа бумаги. Вращение оси счетного колеса регулируется винтами 21 и 22 (см. рис. 17). Следует учесть, что при слишком слабом закреплении оси счетного колеса возможно его колебание. Положение верньера относительно края счетного колеса регулируется винтом 25.
2. Плоскость ободка счетного механизма должна быть перпендикулярна оси счетного колеса. Данная поверка выполняется путем обвода контура некоторого участка на бумаге при двух положениях полюса относительно обводного рычага – справа и слева.
Если результаты разнятся между собой не более, чем на 1/250 среднего значения разностей отсчетов, то считается, что планиметр удовлетворяет установленным требованиям. При больших разностях следует производить измерение площадей при двух положениях полюса относительно обводного рычага и счетного механизма. Среднее значение из двух измерений свободно от погрешностей, вызванных нарушением данного условия.
Для измерения площадей с повышенной точностью применяется планиметр ПП-2К. Он имеет две каретки счетного механизма, расположенные с обеих сторон обводного рычага, и, кроме того, обводный шпиль у этого планиметра заменен обводной точкой, выгравированной на нижней поверхности стекла.
Отметим, что в настоящее время имеются и электронные планиметры с индикацией результата измерений на экране дисплея.
6.2. Измерение площадей планиметром
Планиметр, используемый для измерения площадей, должен удовлетворять рассмотренным выше требованиям. Необходимо также знать его цену деления и постоянное значение величины q. Если эти величины неизвестны, то их можно определить.
Цена деления планиметра – это площадь, соответствующая изменению отсчета на одно деление. Геометрически ее можно представить как площадь прямоугольника, одна из сторон которого равна длине обводного рычага, а другая – делению планиметра. Цену деления можно выразить в квадратных миллиметрах, если надо измерить площадь участка на бумаге, или, например, в гектарах, когда требуется знать значение измеряемой по карте площади на местности. Для определения цены деления планиметра берется участок, площадь которого заранее известна, затем производится измерение указанной площади планиметром. Обычно для этого пользуются квадратом координатной сетки карты со стороной 10 см. Например, площадь квадрата координатной сетки карты масштаба 1:10 000 равна 100 га.
Обводный шпиль сначала устанавливают в центре квадрата, а полюс закрепляют в такой точке, чтобы угол между обводным и полюсным рычагом был равен примерно 90° и чтобы при обводе квадрата ни одна из опорных точек планиметра не выходила за пределы листа карты. Обводный шпиль подводят к одному из углов квадрата и снимают отсчет u1. Далее шпилем обводят стороны квадрата по ходу часовой стрелки. Возвратившись в исходную точку, снимают второй отсчет u2.
Сместив несколько обводное колесо, вторично производят обвод квадрата против часовой стрелки. При движении по ходу часовой стрелки отсчеты будут возрастать, против часовой стрелки – уменьшаться. Вычитая из большего значения меньшее, находят разности отсчетов, которые не должны отличаться более чем на 5 делений. Проведенные измерения составляют один полуприем. Второй полуприем выполняют в положении полюса с другой стороны обводного рычага и каретки счетного механизма. Расхождение в средних разностях отсчетов при двух полуприемах не должно превышать 5 делений. При наличии сходимости за окончательное значение разности отсчетов принимается среднее из двух результатов.
Цена деления планиметра вычисляется по формуле
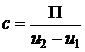 ,
,
где П – площадь измеренного участка; и2 – и1 – средняя разность отсчетов из двух полуприемов.
Цена деления планиметра зависит от положения каретки счетного механизма на обводном рычаге. Перемещая каретку, можно найти такое ее положение, когда значение с будет удобно для измерений, например 1; 0,1; 0,01 и т. п.
Пример. Пусть при обводе квадрата километровой сетки на карте масштаба 1:10000 получена цена деления с = 0,0985 га. Отсчет R по шкале обводного рычага 19 (см. рис. 17) составил 159,1 мм. Удобную цену деления планиметра с0 примем равной 0,1 га. Тогда каретку счетного механизма следует переместить на такую величину, чтобы новый отсчет R0 по шкале обводного рычага был равен
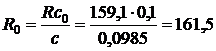 мм.
мм.
Измерение площадей относительно небольших участков (в поперечнике не более 15–17 см) производится с полюсом вне контура. Так же, как и при определении с, шпиль располагают примерно в центре участка, а для полюса выбирают такое место, чтобы рычаги планиметра составляли прямой угол (рис. 18, a). Затем производится беглый обвод контура. Угол между рычагами (рис. 18, б,в) должен составлять не менее 30° и не более 150°. Если это условие не выполняется, то подбирается другое, более благоприятное положение полюса. Возможны случаи, когда это не удается, и угол между рычагами выходит за пределы допуска при любом положении полюса. Тогда измерение площадей следует выполнять с полюсом внутри контура (рис. 18, г) или по частям.
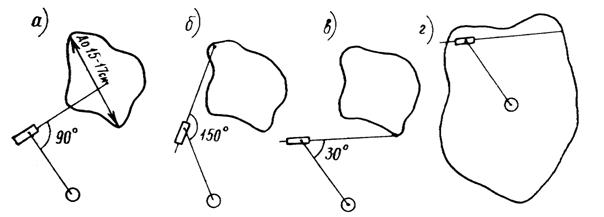
Рис. 18
Измерение площади участка производится полным приемом, так же как при определении цены деления планиметра. При этом контур участка тщательно обводят шпилем четыре раза: по два раза по ходу и против хода часовой стрелки при двух положениях полюса относительно рычага. Возможно также измерение полуприемом.
Расхождения разностей отсчетов в полуприемах допускаются не более 3–4 делений при величине разностей до 1000 делений и 5–6 делений для участков большего размера.
Площадь участка, измеренная при полюсе вне контура, вычисляется по формуле
![]() .
.
Значение q планиметра, необходимое при работе с полюсом внутри контура, определяется так же, как и цена деления с, путем обвода контура участка, площадь которого известна. Участок выбирается значительно больших размеров (квадрат 40 ´ 40 см или круг радиусом 30 см). Значение q находится с учетом ранее установленной цены деления с
![]() .
.
Площадь с полюсом внутри контура определяется одним приемом и к разности отсчетов добавляется q:
П = с(и2 – u1 + q).
Точность результатов измерений планиметром зависит от многих факторов: точности определения постоянных с и q, конфигурации участка, состояния прибора, деформации бумаги и т. д.
Участки с большим периметром и сложными извилистыми границами (полосы дорог, рек и т. п.) надежнее определять графическим способом. Измерения рекомендуется проводить по карте, тщательно расправленной и закрепленной на гладком столе так, чтобы угол между рычагами по возможности приближался к прямому. При этом следует определять и учитывать деформацию бумаги.
Ошибка определения площади находится приближенно по формуле
![]() .
.
Упражнение. Определить значение с и q планиметра. Измерить по карте площади двух-трех участков.
7. ИЗОБРАЖЕНИЕ РЕЛЬЕФА ГОРИЗОНТАЛЯМИ
Рельефом называется совокупность неровностей земной поверхности. При строительстве и эксплуатации различных объектов рельеф часто имеет решающее значение.
Для изображения рельефа предложены различные способы (отмывка, штриховка и т. д.). На современных топографических картах и планах, применяемых для решения инженерных задач, рельеф изображается горизонталями.
Существо метода заключается в следующем. Прежде всего определяется высота характерных точек над уровенной поверхностью (рис. 19). Численное значение высоты точки называется отметкой. Имея отметки характерных точек, по определенным правилам строят горизонтали.
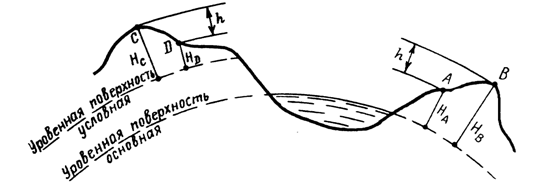
Рис. 19
При проведении практических съемок часто оказывается целесообразным определять отметки не относительно основной, а относительно условно принятой уровенной поверхности. Тогда отметки в первом случае называются абсолютными, во втором – условными (HA, НВ – абсолютные отметки; HD, НC – условные).
В Российской Федерации основная (исходная) уровенная поверхность зафиксирована кронштадтским футштоком. По многолетним наблюдениям за уровнем моря в Кронштадте был установлен средний уровень. В гранитном устое моста через канал закреплена медная пластина, на ней чертой зафиксирован средний уровень. Эту черту именуют нулем кронштадтского футштока. Относительно уровенной поверхности, проходящей через нуль кронштадтского футштока, и определяются абсолютные отметки на всей территории страны.
Условные поверхности (и соответственно условные отметки) применяются для различных участков местности независимо.
Точки физической поверхности Земли характеризуются различными отметками. Но если известны отметки двух точек, то можно вычислить превышение одной точки над другой (относительную высоту). Так, превышение точки В над точкой А (рис. 19) составит: h = НВ – НА. Метод горизонталей позволяет определить отметки любых точек топографической карты или плана. Построение горизонталей осуществляется исходя из следующего.
Пусть имеется некоторая возвышенность (рис. 20, а), которую пересекает поверхность, параллельная уровенной и расположенная от нее на высоте H1. Линия пересечения физической поверхности Земли будет замкнутой кривой и, будучи спроектированной на горизонтальную плоскость, эта линия, называемая горизонталью, характеризует данную возвышенность на отметке H1.
Если для той же возвышенности секущую поверхность примем на высоте H2 (рис. 20, б), то получим другую горизонталь, характеризующую возвышенность на этой высоте.
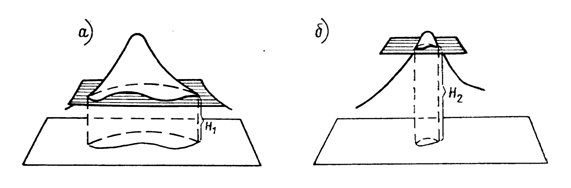
Рис. 20
Для того чтобы получить достаточно детальную характеристику данной формы рельефа, следует задать необходимое количество секущих поверхностей через равные промежутки по высоте hc. (рис. 21). Каждая поверхность и соответственно каждая горизонталь характеризуется определенной отметкой. Отсюда определение: горизонтали – линии, соединяющие точки земной поверхности с одинаковыми отметками.
Расстояние между секущими поверхностями по высоте, т. е. разность отметок двух последовательных горизонталей hc называется высотой сечения рельефа. В зависимости от масштаба, вида рельефа и назначения плана или карты применяют hc = 0,25; 0,5; 1; 2; 2,5; 5 м и др. Чем меньше высота сечения рельефа, тем точнее должны быть выполнены работы по съемке рельефа.
Для изображения отдельных деталей рельефа применяют полугоризонтали, в том случае, если это не удается сделать при помощи основных горизонталей. Их проводят через hc/2, вычерчивают прерывистыми линиями (см. рис. 21).
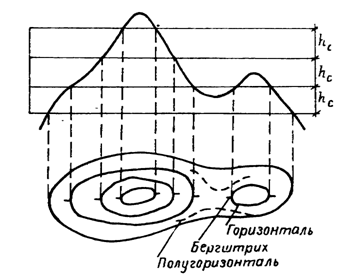
Рис. 21
Горизонтали всегда проводят кратными принятой высоте сечения рельефа. Так, если hc = 0,5 м, то возможны следующие отметки горизонталей: 16,5; 17; 17,5 м и т. п. Если hc = 2 м, то, соответственно: 24; 26; 28 м...
Для лучшего чтения рельефа часть горизонталей вычерчивают утолщенной линией: при hc = 0,25; 0,5; 2,5 м обычно утолщается каждая четвертая горизонталь (соответственно кратные 1; 2; 10 м); при hc = 1; 2; 5; 10 м утолщается каждая пятая или десятая (соответственно кратная 5; 10; 25; 50 м). У утолщенных горизонталей выписывают их отметки, располагая цифры в разрывах горизонталей так, чтобы их верх был направлен в сторону возвышения. Дополнительно направления скатов указывают берг-штрихами (рис. 22).
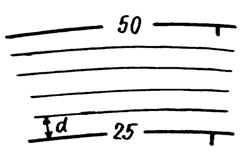
Рис. 22
Расстояние между горизонталями в плане d называется заложением горизонталей (см. рис. 22).
7.1. Свойства горизонталей
1. Горизонтали – замкнутые линии (могут выходить за рамку данного плана и замыкаться за его пределами).
2. Горизонтали не пересекаются. Исключение – нависающие (обратные) скаты.
3. Чем меньше заложение горизонталей d при одинаковом hc, тем круче скат. Линия, образованная наименьшими d, соответствует направлению наибольшей крутизны.
Рельеф в общем случае разделяют на три вида: равнинный – превышения до 30 м; холмистый – превышения до 200 м; горный – превышения более 200 м.
В каждом виде рельефа выделяют пять основных форм: возвышенность, котловину, хребет, лощину и седловину (рис. 23).
1. Возвышенность (гора – высота более 200 м, холм – менее 200 м). Элементы данной формы рельефа: вершина, скаты, подошва.
2. Котловина – замкнутое углубление. Элементы – дно, скаты, бровка.
3. Хребет – вытянутая возвышенность. Элементы – скаты, гребень хребта. Линия, идущая по гребню, называется водоразделом.
4. Лощина – вытянутое углубление. Элементы – скаты, водосливная линия (тальвег, водоток); широкая лощина называется долиной, узкая – ущельем или оврагом.
5. Седловина (перевал) – пониженная часть местности между двумя соседними возвышенностями с расходящимися в противоположные стороны лощинами.
Все формы рельефа образуются из сочетания наклонных поверхностей – скатов. Крутизна ската оценивается или углом наклона (в градусной мере), или величиной уклона i. Уклоном линии называется тангенс угла наклона линии к горизонту: i = tg n = h/d (рис. 24), где h – превышение; d – горизонтальное проложение линии. Угол наклона линии и уклон линии могут быть положительными (+n; +i) или отрицательными (–n; –i).
Для построения горизонталей существуют различные способы. Но при использовании любого из них следуют единому принципу: на участке между двумя соседними характерными точками А и В (рис. 25) линия реальной физической поверхности 1 заменяется условным прямолинейным отрезком 2. После такой замены становится возможным применение линейной интерполяции при определении на плане точек, принадлежащих конкретной горизонтали.
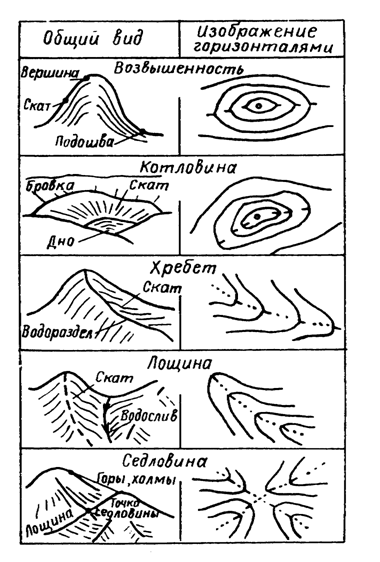
Рис. 23
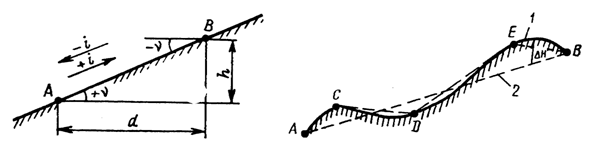
Рис. 24 | Рис. 25 |
Замена реальной линии 1 условной 2 должна осуществляться таким образом, чтобы обеспечивалась необходимая точность изображения рельефа при заданной высоте сечения hc. Требуемая точность Dh во всех случаях задается как часть hc, например: Dh = 1/2hc. Это означает, что во всех случаях замена (при построении горизонталей) линии 1 линией 2 должна обеспечить заданную точность Dh. Пусть, например, hc = 5 м, тогда Dh = 2,5 м и точки А и В (см. рис. 25) выбраны так, что заданная точность гарантируется. Если для этого участка местности принять hc = 1 м (т. е. Dh = 0,5 м), то для обеспечения такой более высокой точности потребуются дополнительные точки С, D, E.
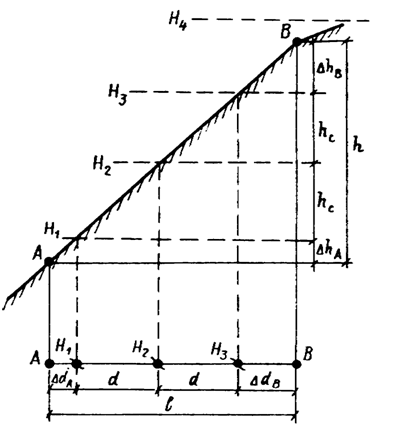
Рис. 26
При съемке рельефа характерные точки (А, В или ACD и т. д.) выбирают там, где уклон ската меняет величину или направление. Чем меньше hc (чем крупнее масштаб), тем больше требуется принимать характерных точек рельефа. После нанесения характерных точек с известными отметками на лист бумаги отыскание местоположения точек, принадлежащих определенной горизонтали, производят интерполированием: аналитически, графически или на глаз. При любом способе интерполирования необходимо определить величину трех различных отрезков (рис. 26): DdA; d; DdB. Пусть имеем на плане две соседние точки А и В. Их отметки таковы, что при данной hc между этими точками пройдут три горизонтали с отметками H1, H2, H3.
Отрезки DdA; d; DdB определяются интерполированием.
7.2. Аналитическое интерполирование
Из подобия соответствующих треугольников получаем:
![]() ;
; 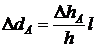 ;
; 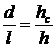 ;
; 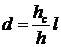 ;
; 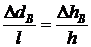 ;
; 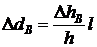 .
.
Пример 1. Пусть отметки точек A и В будут: HA = 12,3 м; HB = 15,6 м. Расстояние между точками на плане l = 56,0 м. Принятая высота сечения рельефа hc = 1 м (рис. 27).
Решение. Между точками А и В пройдут горизонтали с отметками 13; 14; 15 м. Местоположение крайних горизонталей определится отрезками
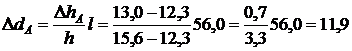 м,
м,
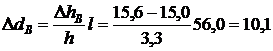 м.
м.
Отложив в масштабе плана от точки А отрезок 11,9 м и от точки В отрезок 10,1 м, получим местоположение горизонталей 13,0 и 15,0. Разделив расстояние между этими крайними горизонталями пополам, находим местоположение горизонтали 14,0.
Пример 2. Пусть при тех же исходных данных hc = 0,5 м. Тогда между точками А и В пройдут горизонтали 12,5; 13,0; 13,5; 14,0; 14,5; 15,0; 15,5. Соответственно
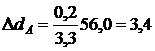 м;
м; 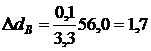 м.
м.
Разделив расстояние между крайними горизонталями на шесть частей, определим местоположение оставшихся пяти горизонталей.
7.3. Графическое интерполирование
Такое интерполирование, по сравнению с аналитическим, позволяет выполнить работу быстрее, с обеспечением необходимой точности. При графическом интерполировании используют интерполятор. Для построения интерполятора на кальке тушью вычерчивают ряд параллельных прямых линий на одинаковом расстоянии одна от другой (через 2, 4, 5 или 10 мм в зависимости от крутизны скатов данной местности и высоты сечения рельефа).
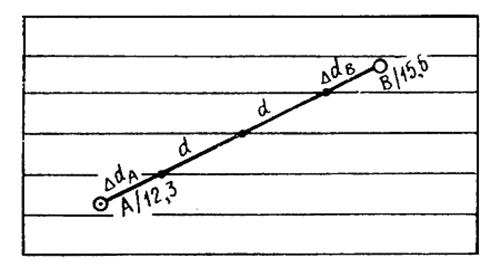
Рис. 27
Для определения местоположения горизонталей интерполятор накладывается так, чтобы число линий интерполятора между точками А и В (см. рис. 27) равнялось числу горизонталей на этом отрезке. Так, при исходных данных рассмотренного выше примера 1 отрезок АВ должны пересекать три линии интерполятора. Затем, поворачивая и смещая интерполятор, необходимо получить такое его положение, чтобы DdA составляло часть заложения d в соответствии с превышением DhA, и одновременно DdB также соответствовало превышению DhB. Оценка приведенных соответствий производится измерениями, при достаточном опыте – на глаз. Фиксировать на плане найденные точки местоположения горизонталей можно наколами иглы (обычно оказывается достаточным надавливание карандашом).
7.4. Интерполирование на глаз
При наличии достаточного опыта определение местоположения горизонталей производят на глаз, руководствуясь теми же положениями, которые приведены в аналитическом методе интерполяции. Практика показывает, что глазомерное интерполирование обычно обеспечивает точность в ¼ hc, что соответствует точности съемки рельефа.
Построение горизонталей заключается в соединении плавными кривыми точек, найденных в результате интерполяции (аналитической, графической или на глаз). Начинать целесообразно с характерных по рельефу форм местности. Водораздельные и водосливные линии пересекаются горизонталями под прямыми углами.
Практическая часть
1. В пределах квадрата километровой сетки по двум сторонам квадрата определите направление повышения и понижения местности, руководствуясь берг-штрихами, надписями горизонталей, отметками характерных точек на карте.
2. Нанесите характерные линии рельефа. Характерными линиями рельефа являются водораздельные и водосливные линии. В центральной части карты опознайте две смежные возвышенности, разделенные лощиной. В пределах квадрата километровой сетки построить водосливную линию и на участках возвышенностей, непосредственно примыкающих к лощине, постройте водораздельные линии. При построении водосливных и водораздельных линий имейте в виду, что они пересекают горизонтали в местах их наибольшей кривизны. Водораздельные линии проходят также через точки с наибольшими отметками и через средние точки седловины.
3. Определите отметки всех горизонталей в пределах заданного квадрата километровой сетки.
8. РЕШЕНИЕ ЗАДАЧ ПО ТОПОГРАФИЧЕСКИМ КАРТАМ
8.1. Определение отметок точек
При решении задач по определению отметок точек возможны следующие пять случаев.
1. Точка К (рис. 28) лежит на горизонтали. Ее отметка определится отметкой горизонтали (Hk = 79,0 м).
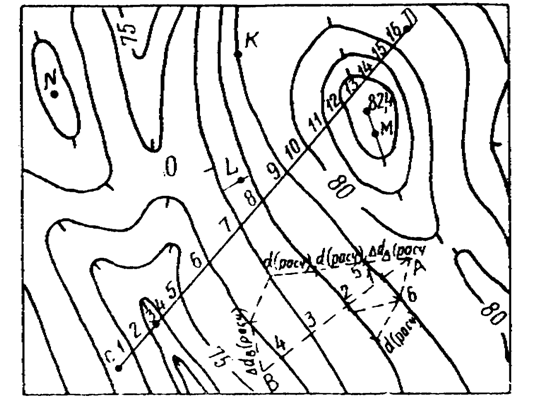
Рис. 28
2. Точка L находится между горизонталями с разными отметками. Проведя через точку L линию кратчайшего расстояния между горизонталями и применив линейную интерполяцию, определяем: HL = 77,6 м.
3. Точка М находится внутри замкнутой горизонтали и известна отметка характерной точки (вершины возвышенности) – 82,4. Проведя через точку с известной отметкой и точку М линию до горизонтали и применив линейную интерполяцию, находим: НМ = 82,2 м.
4. Точка N находится в центре замкнутой горизонтали, отметки характерной точки нет. В подобных случаях следуют правилу: превышение точки в центре замкнутой горизонтали принимается равным половине высоты сечения рельефа. Следовательно, в нашем случае
HN = 78,0 + ![]() = 78,5 м.
= 78,5 м.
5. Точка О находится в точке седловины. Здесь также принимается превышение 0,5hc, тогда НO = 76,5 м.
Отметки точек по топографическому плану или карте вычисляют с точностью 0,1hc.
8.2. Определение крутизны ската
Крутизна ската оценивается посредством измерения угла наклона линии к горизонту n или величины уклона i, та и другая характеристика может быть или положительной, или отрицательной. Обе величины можно вычислить, применив формулу i = tgn = ![]() , или, для ускорения определения n и i, воспользоваться специальными графиками, которые называются масштабами заложений: масштабом заложений для уклонов (рис. 29, а); масштабом заложений для углов наклона (рис. 29, б).
, или, для ускорения определения n и i, воспользоваться специальными графиками, которые называются масштабами заложений: масштабом заложений для уклонов (рис. 29, а); масштабом заложений для углов наклона (рис. 29, б).
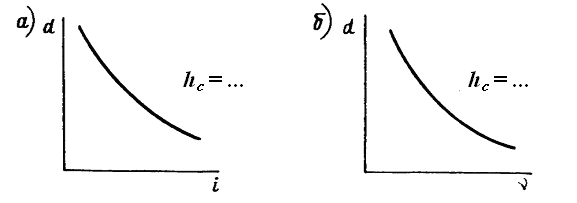
Рис. 29
Масштабы заложений строятся для определенной величины hc. Задаваясь различными значениями заложения горизонталей d (т. е. горизонтальное проложение между смежными горизонталями), можно вычислить угол n пo формуле tgn = ![]() и уклон i =
и уклон i = ![]() , затем построить масштабы заложений ni = f1(di) и ik = f2(dk).
, затем построить масштабы заложений ni = f1(di) и ik = f2(dk).
Для того чтобы по имеющимся масштабам заложений определить крутизну ската, следует в раствор циркуля взять заложение d, приложить к масштабу заложения так, чтобы одна ножка циркуля была на основании шкалы, а другая – на кривой, при этом обе ножки должны быть на перпендикуляре к основанию шкалы.
Уклон является безразмерной величиной, его можно также записать в процентах (%) или в промиллях (o/oo): i = 0,005 = 0,5 % = 5 o/oo .
8.3. Проведение линии по кратчайшему направлению
с уклоном не более заданного (проектного)
Суть задачи: между точками А и В требуется проложить (см. рис. 28) трассу по кратчайшему направлению, но так, чтобы уклон на любом участке трассы был не более некоторого расчетного уклона.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 |




