Расчет разбивочных элементов
Номера точек |
|
|
|
|
|
|
|
|
20 21 | 4257, 50 4358,30 |
=4358,50= =+100,80 | 2590,40 2594,40 |
=2594,40= =+4,00 |
=100,80/4,00= =25,200 |
|
=100,88 |
|
20 А | 4257,50 4308,80 |
| 2590,40 2630,40 |
| 1,283 |
| 65,05 | =354016 |
21 А | 4358,30 4308,80 |
| 2594,40 2590,40 |
| 1,375 |
| 49,52 |
=381758 |
4 5 | 4256,10 4367,80 |
| 3016,60 3012,10 |
| 24,822 | 111,79 |
| |
4 В | 4256,10 . . . |
| 3016,60 . . . |
| ||||
5 В | 4367,80 . . . |
| 3012,10 . . . |
|
|
Тогда тангенс румба линии 20A равен
![]()
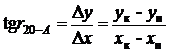 ,
,
где ![]() ,
, ![]() координаты конечной точки линии (в данном случае координаты точки А);
координаты конечной точки линии (в данном случае координаты точки А); ![]() ,
, ![]() координаты начальной точки линии (№ 20).
координаты начальной точки линии (№ 20).
Подставляя исходные данные, получим
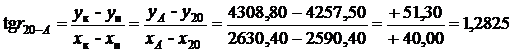 .
.
По знакам приращений координат ![]() и
и ![]() (плюс в числителе и знаменателе) определяем наименование румба линии 20 А: северо-восток. По таблицам приложения находим величину румба следовательно,
(плюс в числителе и знаменателе) определяем наименование румба линии 20 А: северо-восток. По таблицам приложения находим величину румба следовательно, 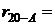 СВ 520323.
СВ 520323.
Для определения угла ![]() необходимо знать также румб линии 20 21. Пусть в результате аналогичных вычислений получено:
необходимо знать также румб линии 20 21. Пусть в результате аналогичных вычислений получено: ![]() СВ: 874339. Тогда
СВ: 874339. Тогда ![]() 874= 354016 (см. рис. 74).
874= 354016 (см. рис. 74).
Горизонтальное проложение линий 20 A вычисляется по формулам
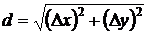 ;
; 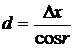 ;
; 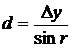 .
.
В данном случае ![]() м.
м.
Контроль: 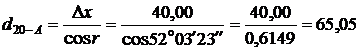 м.
м.
Результаты вычислений представляются в табличном виде (см. табл. 11).
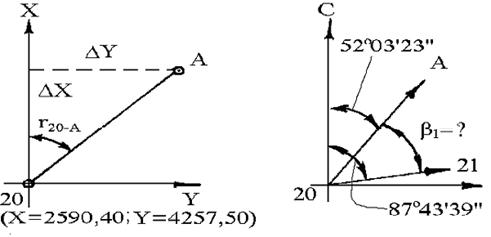
Рис. 73 | Рис. 74 |
Контролем угловых вычислений является равенство 180 суммы внутренних углов треугольников 20 А 21 и 4 В 5 (см. рис. 72), причем значения углов могут быть определены по значениям румбов соответствующих сторон. Так, например, для первого треугольника внутренний угол
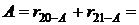 520353 + 535823 = 1060146.
520353 + 535823 = 1060146.
Тогда сумма внутренних углов треугольника равна
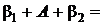 354016 + 1060146 + 381758 = 1800000.
354016 + 1060146 + 381758 = 1800000.
15. Оценка точности геодезических измерений
Измерения подразделяются на прямые и косвенные, однократные и многократные, равноточные и неравноточные.
При прямых измерениях значение искомой величины получается непосредственно по показаниям прибора (например, рулеткой измеряется длина отрезка).
При косвенных измерениях значение искомой величины находится вычислениями по известным формулам на основании данных прямых измерений (например, определение площади треугольника по измеренным основанию и высоте).
Однократные измерения дают одно значение измеряемой величины. При многократных – величина измеряется n > 1 раз. Такие измерения необходимы для контроля, позволяют получить более надежный результат.
Равноточные – измерения выполняются в одинаковых условиях: приборами одинаковой точности, исполнителями одинаковой квалификации, одними и теми же методами и равное число раз, при одинаковых условиях внешней среды.
Неравноточные – измерения, выполненные в неодинаковых условиях и поэтому имеющие разную точность.
Любое измерение сопровождается погрешностями измерения, которые разделяют на грубые, систематические и случайные.
Грубые погрешности (ошибки, промахи, просчеты) выявляют и устраняют контрольными измерениями.
Систематические погрешности искажают результат измерений всегда в какую-либо сторону. Например, мерная лента на величину Dl короче эталона, или известна ее длина при одной температуре, а измерения производятся при другой, и тогда появится систематическая погрешность за счет теплового линейного расширения материала ленты. Систематические погрешности стараются исключить введением поправок.
Случайные погрешности принципиально неустранимы, так как они изменяются случайным образом при повторных измерениях одной и той же величины. Борьба за уменьшение их влияния сводится к совершенствованию приборов и методов измерений, в частности к увеличению числа повторных измерений, к выбору наиболее благоприятных условий работы
Установлены следующие статистические свойства случайных погрешностей.
1. Погрешности по модулю не превосходят некоторого предела
![]() . (15.1)
. (15.1)
2. Равные по модулю положительные и отрицательные погрешности одинаково возможны.
3. Малые погрешности встречаются чаще, чем большие.
4. Среднее арифметическое из погрешностей равноточных измерений стремится к нулю при неограниченном возрастании числа измерений
![]() . (15.2)
. (15.2)
На этих свойствах основана оценка погрешностей и установление наиболее достоверных результатов измерений. Надежную оценку точности измерений – среднюю квадратическую погрешность отдельного измерения – предложил Гаусс:
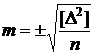 . (15.3)
. (15.3)
В большинстве случаев критерий Гаусса обеспечивает более надежную оценку точности по сравнению со средним арифметическим из абсолютных значений погрешностей ![]() , что можно видеть из следующего примера.
, что можно видеть из следующего примера.
Пример 1. Пусть имеется два ряда измерений при условии, что точность первого ряда заведомо ниже, так как он содержит более значительные по величине погрешности (–6 и +7).
I ряд: –1; +2; –6; +7; –1 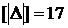 .
.
II ряд: –4; +2; –4; +3; –4 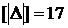 .
.
Тогда ![]() и
и ![]() , то есть получается, что точность обоих рядов одинакова. Но при оценке точности критериев Гаусса получаем
, то есть получается, что точность обоих рядов одинакова. Но при оценке точности критериев Гаусса получаем
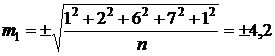 ;
;
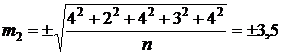 .
.
Видно, что 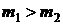 , и наличие в первом ряду больших погрешностей проявилось.
, и наличие в первом ряду больших погрешностей проявилось.
Доказано, что при достаточно большом числе измерений случайная погрешность может быть больше 2m в пяти случаях из ста и больше 3m в трех случаях из 1000. Обычно принимают для более ответственных измерений 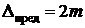 , отбраковывая те результаты измерений, где погрешность больше 2m.
, отбраковывая те результаты измерений, где погрешность больше 2m.
Средняя q, средняя квадратическая m и предельная ![]() погрешности называют абсолютными. Они имеют ту же размерность, что и измеряемая величина.
погрешности называют абсолютными. Они имеют ту же размерность, что и измеряемая величина.
Часто на практике необходимо знать не абсолютную, а относительную погрешность. Например, если одна линия измерена с точностью ![]() (т. е. на 2000 м погрешность составляет 1 м), а вторая с точностью
(т. е. на 2000 м погрешность составляет 1 м), а вторая с точностью ![]() , то, очевидно, что вторая линия измерена точнее. Относительную погрешность обычно представляют дробью, числитель которой равен 1, а знаменатель есть частное от деления измеренной величины на абсолютную погрешность. Так, относительная средняя квадратическая погрешность будет
, то, очевидно, что вторая линия измерена точнее. Относительную погрешность обычно представляют дробью, числитель которой равен 1, а знаменатель есть частное от деления измеренной величины на абсолютную погрешность. Так, относительная средняя квадратическая погрешность будет ![]() . Необходимость оценивать точность измерений возникает в следующих случаях.
. Необходимость оценивать точность измерений возникает в следующих случаях.
1. Истинное значение измеряемой величины X известно заранее, например сумма углов многоугольника. Тогда значение погрешности измерений 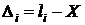 и
и 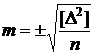 . В практике такой случай встречается редко.
. В практике такой случай встречается редко.
2. Истинное значение измеряемой величины заранее неизвестно. Тогда, по результатам нескольких равноточных измерений, можно определить наиболее вероятное (вероятнейшее) значение измеряемой величины ![]() , которым оказывается арифметическое среднее. Зная
, которым оказывается арифметическое среднее. Зная ![]() , можно вычислить вероятные погрешности (отклонения)
, можно вычислить вероятные погрешности (отклонения) ![]() и по формуле Бесселя среднюю квадратическую погрешность отдельного измерения
и по формуле Бесселя среднюю квадратическую погрешность отдельного измерения 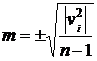 .
.
Но само вероятнейшее значение будет определено также с погрешностью, которую находят по формуле 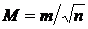 .
.
Пример 2. Даны результаты измерения линии (табл. 12). Оценить точность измерений, т. е. вычислить m, M и ![]() .
.
Т а б л и ц а 12
Исходные данные
Номер измерения | l, м | V, см | v2, см2 |
1 | 68,31 | –1 | 1 |
2 | 68,30 | –2 | 4 |
3 | 68,34 | +2 | 4 |
4 | 68,32 | 0 | 0 |
5 | 68,33 | +1 | 1 |
|
|
|
Решение
![]() м.
м.
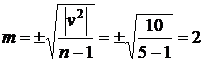 см.
см.
![]() см.
см.
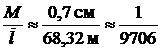 .
.
3. Измеряемая величина определяется косвенным путем, то есть является функцией 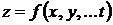 других измеренных с какой-то точностью величин (так называемых измеряемых аргументов), средние квадратические погрешности которых mx; my; … mt.
других измеренных с какой-то точностью величин (так называемых измеряемых аргументов), средние квадратические погрешности которых mx; my; … mt.
В теории погрешностей измерений доказано, что средняя квадратическая погрешность величины ![]() выражается следующей формулой
выражается следующей формулой
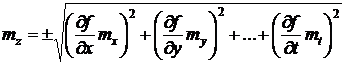
Пример 3. В треугольнике на плане измерено основание ![]() м с
м с ![]() см и высота
см и высота ![]() м с
м с ![]() см. Определить относительную среднюю квадратическую погрешность площади треугольника
см. Определить относительную среднюю квадратическую погрешность площади треугольника ![]() .
.
Площадь треугольника участка равна
![]() м2.
м2.
Найдем частные производные от функции S по аргументам b и h.
![]() ;
; 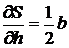 .
.
Тогда
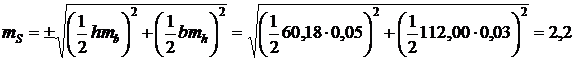 м2
м2
и
![]() .
.
Сведения, приведенные в данном пособии, являются дополнением к основным темам, изучаемым на лекциях. Они позволяют студентам получить практические навыки в решении конкретных инженерных задач по планам и картам.
Библиографический список
1. Инженерная геодезия: Учебник для вузов / ,
, , ; Под ред. . 4-е изд., испр. М.: Изд. центр «Академия», 20с.
2. Инженерная геодезия. Решение инженерных задач на планах и картах: Учеб. пособие / , , . СПб.: Изд-во Политехн. ун-та, 20с.
3. Инженерная геодезия. Расчетно-графические задания: Учеб. пособие / , , . СПб.: Изд-во СПбГТУ, 19с.
4. Инженерно-геодезические измерения: Метод. указания / Сост. , . Л.: Изд-во ЛПИ, 19с.
5. Топографические карты и планы: Метод. указания / Сост. , . Л.: Изд-во ЛПИ, 19с.
6. Топографические планы и карты: Метод. указания / Сост. , . Л.: Изд-во ЛПИ, 19с.
ОГЛАВЛЕНИЕ
Введение . | 3 | ||
1. | Форма и размеры Земли | 3 | |
2. | Общие понятия о картах, планах и профилях | 8 | |
3. | Масштабы | 11 | |
Практическая часть. | 15 | ||
4. | Условные знаки | 16 | |
Практическая часть. . | 17 | ||
5. | Измерение отрезков | 18 | |
Практическая часть. | 20 | ||
6. | Измерение площадей . . . | 20 | |
6.1. | Устройство и поверки планиметра | 23 | |
6.2. | Измерение площадей планиметром | 25 | |
7. | Изображение рельефа горизонталями | 28 | |
7.1. | Свойства горизонталей | 32 | |
7.2. | Аналитическое интерполирование | 35 | |
7.3. | Графическое интерполирование | 36 | |
7.4. | Интерполирование на глаз. . . | 37 | |
Практическая часть. | 37 | ||
8. | Решение задач по топографическим картам | 38 | |
8.1. | Определение отметок точек. . | 38 | |
8.2. | Определение крутизны ската. | 39 | |
8.3. | Проведение линии по кратчайшему направлению с уклоном не более заданного (проектного | 40 | |
8.4. | Построение профиля по заданному направлению | 41 | |
8.5. | Определение границы водосборной площади. . . | 42 | |
Практическая часть. | 42 | ||
9. | Определение планового положения точек земной поверхности | 47 | |
9.1. | Географические координаты. | 47 | |
9.2. | Зональная система плоских прямоугольных координат | 48 | |
Практическая часть. | 51 | ||
10. | Ориентирование линий, планов и карт . . . | 53 | |
Практическая часть. | 58 | ||
11. | Номенклатура топографических карт | 59 | |
11.1. | Разграфка и номенклатура топографических карт | 59 | |
11.2. | Определение номенклатуры топографической карты | 64 | |
12. | План по материалам теодолитной съемки | 66 | |
13. | Проект вертикальной планировки (проектирование горизонтальной площадки) | 73 | |
Практическая часть. | 86 | ||
14. | Расчет разбивочных элементов для перенесения проектной линии в натуру | 88 | |
14.1. | Вычисление исходных данных | 89 | |
14.2. | Составление разбивочного чертежа. . | 91 | |
15. | Оценка точности геодезических измерений | 97 | |
Библиографический список | 102 | ||
МИХАЛЕНКО Евгений Борисович
ЗАГРЯДСКАЯ Наталия Николаевна
БЕЛЯЕВ Николай Дмитриевич
ВИЛЬКЕВИЧ Валентин Войтехович
ДУХОВСКОЙ Федор Николаевич
СМИРНОВ Александр Александрович
ИНЖЕНЕРНАЯ ГЕОДЕЗИЯ
Решение основных инженерных задач на планах и картах
Учебное пособие
Редактор
Технический редактор
Оригинал-макет подготовлен авторами
Директор Издательства Политехнического университета
Свод. темплан 2006 г.
Лицензия ЛР № 000 от 07.08.97
Налоговая льгота – Общероссийский классификатор продукции ОК 005–93, т. 2;
95 3005 – учебная литература
___________________________________________________________________________
Подписано в печать Формат 60x84/16.
Усл. печ. л. Уч.-изд. л. Тираж 100. Заказ
___________________________________________________________________________
Санкт-Петербургский государственный политехнический университет.
Издательство Политехнического университета, член Издательско-полиграфической ассоциации университетов России.
Адрес университета и издательства: Санкт-Петербург, Политехническая ул., 29.
[1] В прямоугольной системе значение координат принято выражать в метрах. При проведении измерений в данном случае допускается выражать координаты в километрах.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 |




