Курс лекций по высшей геодезии (стр. 4 )

Положение любой точки на поверхности эллипсоида также может быть определено пространственными прямоугольными координатами

(

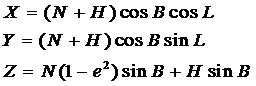Если система координат референцная, то начало этой системы относительно центра масс Земли определяется величинами: X0, Y0, Z0.

Пусть необходимо найти новую референцную систему из градусных измерений, в которой пространственные прямоугольные координаты точек получат новые значения: X+dX, Y+dY, Z+dZ. Изменения прямоугольных координат dX, dY, dZ при сохранении параллельности оси вращения и плоскости экватора одинаковы для всех пунктов сети и вызваны изменениями параметров эллипсоида da, da и геодезических координат dB, dL, dH.

Это может быть выражено дифференциальными уравнениями, в которых дифференциалы параметров эллипсоида и геодезических координат заменены их конечными и малыми приращениями:

(

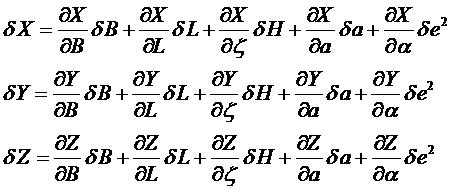Имея формулы связи между сжатием и эксцентриситетом

,

при необходимости несложно получить связь между их дифференциалами или поправками

(

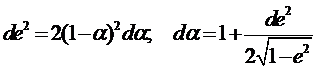Частные производные в (вычисляем из уравнений (, имея в виду выражение для радиуса первого вертикала

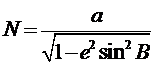
Производя вычисление частных производных и заменяя дифференциальные приращения переменных конечными приращениями – поправками, получаем:

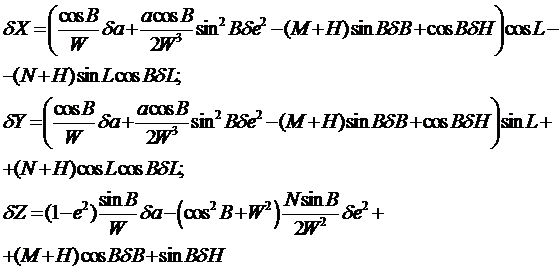
Здесь несложно заметить выражения соответствующих частных производных для (, полученных дифференцированием (по соответствующим переменным.

Решим уравнения (относительно изменений геодезических координат dB, dL, dH . Для этого из первых двух уравнений находим

(

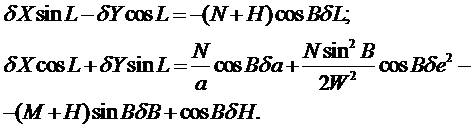Из первого уравнения (находим поправку dL. Для определения поправок dB и dH решаем совместно второе уравнение (с третьим уравнением (:

(

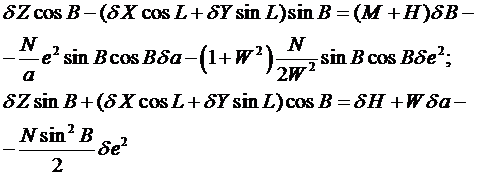Выражая в явном виде поправки dB, dL, dH , получаем:

(

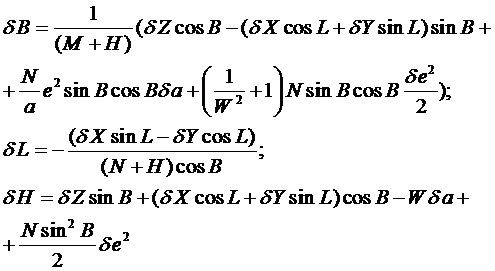Если уравнения (применить для исходного пункта, на котором устанавливаются исходные геодезические даты, то будем иметь

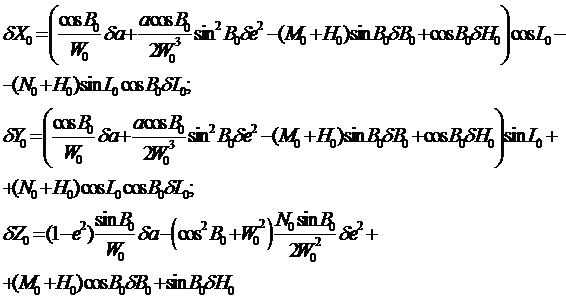(6.32)

Здесь величины dX0,, dY0, dZ0 представляют собой поправки в координаты центра референц-эллипсоида, наиболее подходящего для данной территории.

Из (выражаем в явном виде составляющие уклонения отвеса и аномалию высоты

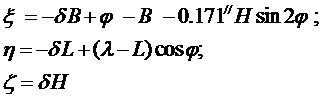
Выражения для поправок в геодезические координаты берем из (, в результате получаем уравнения градусных измерений в методе площадей, в которых роль неизвестных параметров играют поправки к приближенным значениям параметров эллипсоида da, de2 и приближенным координатам его центра dX0,, dY0, dZ0. Составляющие уклонений отвеса и аномалии высот при хорошо подобранном эллипсоиде должны носить случайный характер.

(

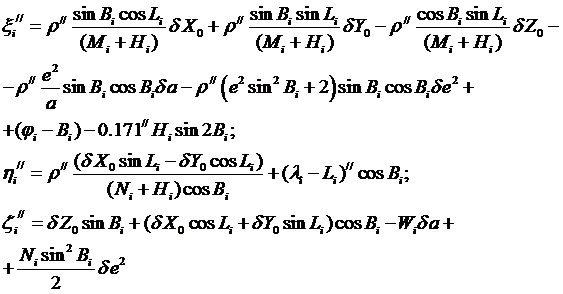Таких уравнений будет столько, сколько астрономо-геодезических пунктов участвует в градусных измерениях ( i = 1, 2. 3, …n ). Решают первые два уравнения под условием

,

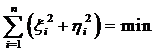а третье уравнение – под условием

.

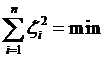Рассмотренный метод строгий и может применяться при выводе параметров земного эллипсоида с использованием спутниковых измерений.

6. 5. Исходные геодезические даты и методы их установления

Как уже отмечалось ранее, исходные геодезические даты определяются выражениями (и задают ориентировку референц-эллипсоида в теле Земли так, чтобы его поверхность наилучшим образом подходила к части поверхности геоида соответствующей территории. Этой частью может быть территория государства или группы государств.

Здесь на некотором пункте, принятом за начальный для государственной геодезической сети, выполнены высокоточные астрономические измерения широты, долготы и азимута, из высокоточного нивелирования и гравиметрических измерений определена нормальная высота. Необходимо определить для этого пункта составляющие уклонений отвеса и аномалию высоты. Другими словами, необходимо выполнить ориентирование поверхности референц-эллипсоида с параметрами, полученными из градусных измерений, в теле Земли так, чтобы имели место минимально возможные и случайные отступления поверхности эллипсоида от геоида на территории государства. При этом, определяя исходные геодезические даты, сохраняют параллельность оси вращения и плоскости экватора референц-эллипсоида по отношению к оси вращения и плоскости экватора реальной Земли на некоторую эпоху. Это имеет принципиально важное значение потому, что в процессе суточного вращения Земли ее ось совершает колебательные периодические движения ( движение полюсов ). Имеют место вековые, обусловленные глобальными изменениями в земном теле и короткопериодические движения полюсов ( период около 430 суток, амплитуда до 0. 3// ), обусловленные геодинамическими и атмосферными явлениями.

Принцип организации вычислений для установления исходных геодезических дат такой же, как и при градусных измерениях. Отличие состоит в том, что для вывода параметров земного эллипсоида учитывают градусные измерения, выполненные на всей поверхности Земли, а для установления исходных геодезических дат – только градусные измерения, выполненные на той территории, относительно которой производят ориентирование референц-эллипсоида.

Так, например, параметры эллипсоида Красовского получены в СССР в 40-е годы XX столетия из совместной обработки градусных измерений, выполненных к тому времени во всем мире. Следует отметить, что к этому времени были известны и другие результаты определений параметров земного эллипсоида, полученные в США и ведущих европейских странах. Но для установления исходных геодезических дат для территории СССР необходимо было решить задачу ориентирования референц-эллипсоида. Эта задача была решена по методу площадей из астрономо-геодезической сети 1 класса, построенной на территории СССР с использованием материалов гравиметрической съемки по европейской части страны. Для территории СССР, расположенной восточнее Урала, определялись топографо-изостатические уклонения отвеса.

Для государств, расположенных в безаномальных районах и имеющих сравнительно небольшие по площади территории, ориентирование референц-эллипсоида может быть выполнено только по одному пункту, принятом за исходный и в котором исходные геодезические даты имеют выражения, следуемые из (

В данном случае поверхность референц-эллипсоида в исходном пункте касается поверхности геоида, ось его вращения параллельна оси вращения Земли. Для малых территорий и в случае отсутствия больших аномалий силы тяжести отступление поверхности референц-эллипсоида от поверхности геоида будут незначительными и редуцироваение измеренных величин на поверхность эллипсоида производится с достаточной точностью методом развертывания.

7. УРАВНИВАНИЕ ГОСУДАРСТВЕННЫХ ГЕОДЕЗИЧЕСКИХ СЕТЕЙ

7. 1. Постановка задачи и пути ее решения

В соответствии со схемой и программой построения государственной геодезической сети СССР в качестве главной плановой геодезической основы, закрепляющей на земной поверхности принятую систему координат (СК – 42), является астрономо-геодезическая сеть полигонов первого класса. Каждый полигон, как известно, состоит из четырех звеньев треугольников триангуляции (иногда трилатерации или полигонометрии). Каждое звено длиной от 200 до 250 км опирается на пункты Лапласа, базисные стороны и состоит из 16 треугольников. Размеры территорий, покрываемые первоклассными полигонами, могут достигать значительных величин, их отображение на плоскости проекции Гаусса-Крюгера в одной координатной зоне невозможно с необходимой точностью. Поэтому астрономо-геодезические сети первого класса уравнивают на поверхности земного эллипсоида, а не на плоскости геодезической проекции.

Государственная геодезическая сеть Республики Беларусь является фрагментом сети СССР, поэтому полезно проследить, как решалась задача построения и уравнивания государственной астрономо-геодезической сети (АГС) СССР. При этом следует отметить, что по своим размерам и точности построения эта сеть не имела мировых аналогов.

Выдающуюся роль в решении задачи уравнивания АГС принадлежит коллективу советских ученых, под руководством . При этом был использован самый передовой мировой опыт, в частности, исследования выдающегося немецкого ученого астрономо-геодезиста . Здесь необходимо было решить две основные проблемы: во-первых, редуцировать измеренные величины без существенных деформаций с физической поверхности Земли на поверхность эллипсоида; во-вторых, сократить объем вычислений без существенных нарушений требований метода наименьших квадратов. Первая проблема решалась применением метода проектирования на достаточно хорошо ориентированный референц-эллипсоид, а вторая – применением полигонального метода уравнивания на основе математически обоснованного перехода от измеренных величин (базисных сторон и углов треугольников, азимутов, широт и долгот на пунктах Лапласа) к длинам и азимутам диагоналей звеньев.

Переход к уравниванию не самих измеренных величин, а их функций, был вынужденной мерой, существенно сокращающей объем вычислений. Следует помнить, что вычисления выполнялись либо с помощью логарифмичесих таблиц, либо на арифмометрах. В настоящее время с использованием высокопроизводительных ЭВМ и соответсвующего программного обеспечения проблемы объема и трудоемкости вычислений практически не существует. При уравнивании АГС СССР реализовано три программы.

Первая программа разработана и применена к уравниванию первых девяти первокласных полигонов в 1930 – 32 гг. Уравнивание проводилось на поверхности эллипсоида Бесселя с исходными геодезическими датами в Пулково. Редукционная проблема вынужденно решалась по методу развертывания (не учитывались поправки за уклонения отвеса и аномалии высот из-за отсутствия информации о них).

Вторая программа также носит имя Красовского и реализована в 1941 – 46 гг. для уравнивания 87 полигонов АГС, включавших 310 первоклассных звеньев. Здесь уравнивание проводилось на поверхности референц-эллипсоида Красовского, параметры и ориентировка в теле Земли были получены к этому времени из градусных измерений. Редуцирование измерений производилось по строгому методу проектирования. Центры порядка 6 000 пунктов АГС 1 класса после уравнивания закрепляли на земной поверхности новую систему геодезических координат, известную как СК – 42.

Современная программа уравнивания АГС СССР разрабатывалась на основе анализа качества построения полигонов 1 и сплошных сетей 2 класса, реализована в 90-х годах прошлого столетия и принципиально отличается от двух предыдущих. Прежде всего, на всей территории СССР завершены работы по созданию не только полигонов первого класса АГС, но и полностью завершены работы по созданию сплошной сети второго класса, заполняющей первоклассные полигоны. Выполнены принципиально новые определения базисов большой протяженности методами спутниковой геодезии. Разработаны методы и алгоритмы уравнивания на ЭВМ обширных геодезических построений с учетом особенностей и специфики создания АГС СССР. Здесь уравниванию подлежали порядка пунктов 1 – 2 классов, объединенных в 277 первоклассных полигонов. Эти пункты закрепляют на земной поверхности модернизированную референцную систему координат СК – 42, которую назвали СК – 95. По нашему мнению более корректно было бы ее назвать СК – 42/ потому, что в ней координатной поверхностью служит референц-эллипсоид Красовского, исходные геодезические даты в Пулково также сохранены. Это не совсем понятно потому, что к этому времени были известны параметры земного эллипсоида и общеземные системы координат, полученные спутниковыми методами в США ( WGS – 84 ) и в РФ ( ПЗ – 90 ).

В настоящее время актуальной является задача модернизации существующих АГС с использованием новых спутниковых технологий координатных определений. При этом следует иметь в виду, что точность взаимного положения пунктов 1 – 2 классов после уравнивания АГС СССР составляет в среднем порядка 7 – 10 см. Современные спутниковые технологии позволяют определять взаимное положение пунктов, удаленных друг от друга до 20 км, с точностью 0,7 – 1,0 см. Таким образом видим, что в настоящее время существуют предпосылки и возможности для создания более высокоточной государственной геодезической основы, чем это было возможно наземными классическими методами. Здесь весьма важным элементом является согласование общеземной системы координат спутникового позиционирования и референцной системы координат СК – 95.

7. 2. Полигональное уравнивание сети 1 класса

Как уже отмечено ранее, первая программа полигонального уравнивания применена к уравниванию 9 полигонов триангуляции 1 класса. Эта программа предполагала три этапа уравнительных вычислений.

На первом этапе производилось уравнивание за все условия, возникающие в отдельном звене: фигур, полюсов, горизонтов, а также азимутов, базисов. Координатные условия ( широт и долгот ) в уравнивание не включались из-за низкой точности ( 0,3// в определении широты и долготы дает ошибку в положении пункта Лапласа порядка 10 – 12 м. ). В результате уравнивания на первом этапе получали предварительно уравненные углы тругольников.

Решая по исходной длине и предварительно уравненным углам треугольники триангуляции 1 класса (по теореме Лежандра или способу аддитаменто), вычисляли длины всех сторон. Последовательно решая прямую геодезическую задачу от начального пункта Лапласа (для которого установлены исходные геодезические даты) до конечных пунктов в звеньях, получают их широты и долготы. По мере удаления от геодезического пункта с исходными датами, в качестве исходного пункта принимали ранее определенный. Затем, решая обратную геодезическую задачу между начальным и конечным пунктами каждого звена, вычисляли длину и азимуты его диагонали. Результатом первого этапа получали сеть полигонометрии, стороны которой - диагонали звеньев, порядка 200 – 250 км, а углы – разности их азимутов. Ошибки в длинах и углах поворота этой полигонометрии не являются независимыми и случайными ошибками измерений, хотя зависят от них.

На втором этапе уравнивают систему образовавшихся полигонов за возникающие условия (координатные и азимутальные). Получают уравненные значения длин и азимутов геодезических линий – сторон полигонов, по которым вычисляют окончательные значения координат вершин полигонов (пунктов Лапласа). Здесь нарушается требование метода наименьших квадратов, т. к. уравниваются не измеренные величины, а их функции.

На третьем этапе производят вставку отдельных звеньев между пунктами Лапласа с уравненными координатами, с присоединением азимутального и базисного условий. Результатом являлись окончательные координаты всех пунктов звена первого класса. Здесь проблема состояла в том, что углы треугольников, образующих центральную систему в местах пересечения звеньев, получали разные поправки из разных звеньев. Для устранения этого противоречия каждая такая центральная система уравнивалась отдельно, и значения углов в ней считались окончательными.

Анализ материалов уравнивания 9 полигонов по указанной методике показал вполне удовлетворительные результаты. Вместе с тем, уже к началу 40-х годов ХХ столетия существенно возрос объем выполненных измерений на значительно большей территории страны. Были выполнены градусные измерения, по результатам которых были получены новые параметры эллипсоида, произведена его ориентировка в теле Земли (референц-эллипсоид Красовского). Существенно пополнился банк данных гравиметрических маятниковых измерений, что позволило на значительной части территории страны вычислить астрономо-гравиметрические уклонения отвеса. Применяя гипотезу изостазии, вычислили топографо-изостатические уклонения отвеса для удаленных от центра восточных территорий. Все это позволило применить строгий метод развертывания при редуцировании измерений.

В новых условиях существенно большего объема измерительной информации обнаружили, что уравнивание в полном соответствии с первой программой не может принести удовлетворительных результатов. Нужно было каким–то образом объяснить и избавиться от существенных значений невязок азимутальных условий, которые преимущественно приближались к предельно допустимым значениям или даже их превышали. Здесь явно имело место наличие систематических ошибок азимутальных определений на пунктах Лапласа.

Вторая программа уравнивания была разработана с учетом опыта первого уравнивания. 87 первоклассных полигонов, из которых только 11 полигонов образовывали узкую цепь от Красноярска до Хабаровска, уравнивались также полигональным методом, как и в первой программе, только первый этап разделили на три, чтобы избавиться от больших невязок азимутальных условий.

На первом этапе уравнивание звеньев за условия фигур, полюсов и базисов, в результате получали предварительно уравненные углы.

На втором этапе составление азимутальных уравнений по каждому звену по предварительно уравненным на первом этапе углам, совместное решение всех азимутальных условий с нахождением поправок в астрономические азимуты и долготы на пунктах Лапласа.

На третьем этапе производилось вторичное уравнивание звеньев триангуляции по непосредственно измеренным направлениям за условия фигур, полюсов, базисов и азимутов. Здесь при составлении азимутальных условий астрономические долготы и азимуты исправляются поправками, вычисленными на втором этапе. В результате вычисляют длину и азимут геодезической линии для каждого звена триангуляции первого класса.

На четвертом этапе производят уравнивание полигонов и окончательное вычисление координат их вершин.

На пятом этапе производят вставку звеньев между вычисленными координатами их вершин, исходными азимутами Лапласа и базисными сторонами (уравнивание звена за все возникающие в нем условия: фигур, полюсов, базисов, азимутов и координат ).

7.  3. Современное уравнивание астрономо - геодезической сети 1 – 2 классов

По мере заполнения полигонов первого класса сплошными сетями второго класса возникла проблема их уравнивания. На первоначальном этапе сети второго класса уравнивались как опирающиеся на исходные пункты первого класса. В отдельном полигоне насчитывалось более 500 определяемых пунктов второго класса, при уравнивании приходилось решать системы с 1000 и более нормальных уравнений. Здесь применялся многогрупповой метод уравнивания -Праневича, идея которого была предложена еще Ф. Гельмертом. Суть этого метода состоит в том, что преобразованные нормальные уравнения при последовательном исключении неизвестных в алгоритме Гаусса эквивалентны исходным, и при соответствующем разделении на группы их можно решать раздельно. При этом не нарушается строгость решения задачи уравнивания и к уравнительным вычислениям можно привлекать параллельно столько вычислителей, сколько образовано групп уравнений.

В процессе уравнивания обнаружилось, что поправки в измеренные величины на пунктах второго класса распределялись не случайно, а по вполне определенным закономерностям. В середине полигона поправки соответствовали точности измерений и носили случайный характер, а по мере приближения к исходным пунктам первого класса они возрастали и достигали величин, существенно превышающих возможные ошибки измерений. Это говорило о том, что пункты первого класса по точности не могут служить исходными для сети второго класса. Действительно, средние квадратические ошибки измерения углов в триангуляции 1 и 2 класса соответственно равны 0, 7// и 1, 0//, что практически одно и то же, но сплошные сети второго класса гораздо более жесткие по сравнению с полигонами первого класса. Это подтверждалось и тем, что при уравнивании сетей второго класса, как свободных, поправки из уравнивания получали случайные значения, соответствующие точности измерений.

Для устранения такого противоречия необходимо было производить совместное уравнивание сети из пунктов 1 – 2 классов как сплошной с соответствующими весами измерений. Это впервые было обосновано профессором

Но буквально до 80-х годов ХХ столетия в геодезических вычислениях оставалась проблема объема вычислений из-за отсутствия соответствующей вычислительной техники. Поэтому предлагались различные варианты упрощенных методов решения задачи. Один из них основан на усовершенствовании первого этапа полигонального метода путем усиления первоклассных звеньев смежными треугольниками второго класса и их совместное уравнивание (сдвоенных, строенных и т. д. рядов треугольников). Обсуждался метод, предложенный венгерским геодезистом Рёгеци. Суть его состоит в замене сплошной сети треугольников триангуляции треугольниками, образованными из замыкающих первоклассных звеньев и диагоналей полигонов, уравнивание такой сети глобальных треугольников, результатом которого являются уравненные координаты пунктов, являющихся вершинами этих треугольников, а также значения углов и длин их сторон. Эти предложения не были реализованы в полной мере на практике по следующим причинам: во-первых, из-за большого объема вычислений; во-вторых, из-за существенных отступлений от требований метода наименьших квадратов; в-третьих, не было отдано предпочтение какому-либо одному методу. Вместе с тем, следует отметить результаты практической апробации полигонального уравнивания с усилением первоклассных звеньев треугольниками второго класса, приведенные в таблице 7.1. Здесь были обработаны к 1964 году 402 полигона с 978 звеньями, включающихпунктов. Полигоны включали 2 434 азимута Лапласа и 1 600 базисов.

Таблица 7. 1

Результаты сравнения координат пунктов АГС СССР, уравненных по второй программе Красовского в 40-ые годы и с усилением первоклассных звеньев треугольниками 2 класса в 60-ые годы, показали расхождения до 20 метров на Востоке страны. Это можно объяснить систематическими ошибками редуцирования по методу развертывания, применяемого в 40-е годы, ошибкой в исходном азимуте в Пулково, ошибками долготных определений, слабой геометрической жесткостью рядов 1 класса. Однако более детальный анализ изменения координат по всей территории страны показал неравномерность распределения этих разностей и их привязку к геологическим разломам и сейсмически активным районам. Следовательно, наиболее вероятной причиной и наиболее значимой составляющей изменения координат могут быть геодинамические явления.

Первым опытом уравнивания АГС 1 – 2 классов, как сплошной сети, было уравнивание астрономо-геодезической сети стран Варшавского договора ( ЕАГС ), расположенной на территории СССР западнее первоклассного ряда Пулково-Николаев, далее на территории Польши, Болгарии, Восточной Германии, Венгрии, Чехословакии, Румынии (частично). Всего в данной сети насчитывалосьпунктов. Работы выполнялись в гг. Было два предложения по методам решения нормальных уравнений при строгом уравнивании: польского ученого Банахевича и сопряженных градиентов. Апробация этих методов проводилась на опытной сети, состоящей из 865 пунктов. Были получены идентичные результаты, и для уравнивания всей сети был избран метод сопряженных градиентов с исходным пунктом в Пулково. В уравнивание был включен полигонометрический траверс Пулково-София-Потсдам-Пулково. Уравнивание ЕАГС выполнялось на большой ЭВМ ЕС – 1033 в АГП №7 (г. Москва).

По материалам уравнивания были получены характеристики ЕАГС, приведенные в таблице 7. 2

Таблица 7. 2

Ошибка взаимного положения между смежными пунктами этой сети на территории СССР составляла порядка 4 -5 см. Здесь впервые было обнаружено, что исходный азимут для АГС СССР Саблино-Бугры, определенный в 1926 году, имеет ошибку порядка 4// - 5//, что являлось недопустимо грубой величиной и получило подтверждение из повторных высокоточных астрономических определений этого азимута в 1981 г.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5