Рис. 5. 1
Таким образом, точность вычисления редукционной поправки не должна превышать относительной величины 1 : 4 Данный метод линейных измерений ушел в историю, вместе с тем мы рассмотрим редуцирование базиса, что интересно с методической точки зрения.
Мерным элементом базисного прибора 1 класса служит комплект из четырех компарированных инварных струн, на концах которых специальные инварные шкалы с полумиллиметровыми делениями для снятия отсчетов. Общая длина прибора составляет 24 м. и называется базисным пролетом. В процессе измерений определяются превышения концов каждого пролета методом геометрического нивелирования. Схематически пролет изображен на рисунке 5. 2.
 |
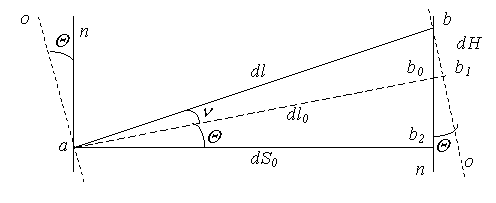Рис. 5. 2
На рисунке имеем: dl – измеренная длина пролета; dl0 – горизонтальное проложение; dS0 – эллипсоидальное проложение; Q - составляющая уклонения отвеса в направлении базиса; n - угол наклона пролета к горизонту; о – направление отвеса; n – направление нормали; dH – превышение концов пролета. Длина пролета малая, поэтому можно считать направления отвеса на его концах параллельными. Параллельны также направления нормали. Для прямоугольного при вершине b2 треугольника abb2 запишем
,
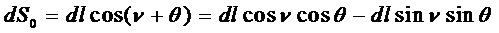где также имеем:
,
поэтому, учитывая малые значения Q , разлагая тригонометрические функции этого аргумента в ряд с удержанием только первого члена, можем записать с достаточной точностью
Таким образом вычисляют эллипсоидальную длину каждого пролета dS0i из уложившихся вдоль базиса. При этом получают длины, отнесенные на поверхности, параллельные поверхности референц-эллипсоида и расположенные на средней высоте Hi каждого пролета. Схематично это показано на рисунке 5. 3.
 |
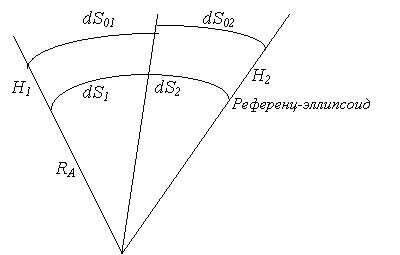Рис. 5. 3
Для получения проекции на поверхность эллипсоида dSi каждого из отрезков dS0i следует из рисунка формула
(
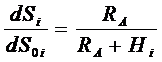где RA – радиус нормального сечения, проходящего в азимуте базиса.
Далее получаем для эллипсоидального проложения базисного пролета
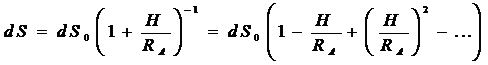
С учетом выражения (имеем
(
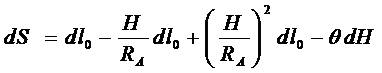Как отмечено ранее, длина базиса порядка 10 км. В этом случае можно считать поверхность эллипсоида совпадающей с поверхностью шара радиусом RA и далее получаем для всей длины базиса, средняя высота которого равна Hm
(
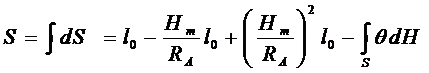Выразим относительную величину поправки
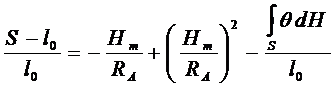
и оценим значения поправочных членов в этой поправке. Для расчетов примем следующие значения элементов полученной формулы: Hm £ 1000м, l »м, превышения вдоль базиса DH £ 100 м., уклонения отвеса Q £ 5//. В этом случае первый поправочный член не превзойдет величины 1 : 6 400; второй – 1 :, третий – 1 : 4 При этих условиях необходимую точность редуцирования ( 1: 4 обеспечит простая формула
(
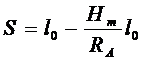Значения средней высоты Hm и радиуса RA достаточно вычислять с точностью, рассчитанной по известному принципу равных влияний
;
;
;
.
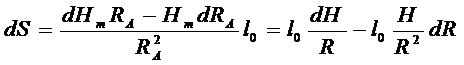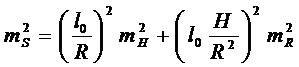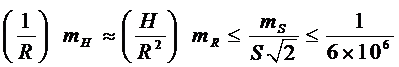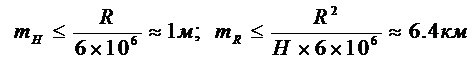Отсюда видно, что для решения редукционной проблемы высоты необходимо знать с точностью до метров, а средний радиус кривизны эллипсоида – до нескольких километров. Эти требования к точности высот и радиуса невелики, что существенно облегчает решение данной задачи, в особенности на первоначальном этапе построения государственных опорных геодезических сетей.
5. 3 Редукция свето и радиодальномерных измерений.
В настоящее время линейные измерения производятся, в основном, свето и радиодальномерами, которые постоянно совершенствуются. Приборные погрешности измерений могут быть сведены до миллиметров, и главным сдерживающим фактором является влияние внешних условий. В спутниковых системах позиционирования реализованы радиодальномерные измерения, выполняемые вдоль направлений геодезические спутники – носители координат из созвездий NAVSTAR (США) или ГЛОНАСС (РФ) – приемники, расположенные на пунктах, координаты которых определяются из пространственной линейной засечки. Точность координатных определений, как абсолютные, так произведенных посредством спутниковых систем на порядок выше, по сравнению с классическими наземными методами ( астрономо-геодезическими). Это стало возможно за счет того, что измерения вынесены за пределы топографической рефракции в область астрономической, что позволило уменьшить влияние внешних условий на точность измерений.
Рассмотрим редуцирование наземных измерений, производимых в полигонометрии, трилатерации и масштабировании триангуляции при построении государственных опорных сетей. Здесь измеренные расстояния между смежными пунктами могут достигать от 20 до 30 километров. Относительная погрешность измерений характеризуется величиной 1 : 400 000, следовательно, редукционные поправки необходимо вычислять с точностью на порядок выше, следовательно 1 : 4 000 000. Это требование необходимо выполнять для того, чтобы ошибки округления при вычислениях (подчиняющиеся равномерному закону распределения) не наложились на ошибки измерений (подчиняющиеся нормальному закону распределения) и математическую обработку редуцированных величин можно было производит по методу наименьших квадратов.
 |
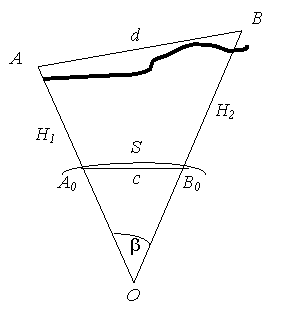Рис. 5. 4
На рисунке 5. 4 имеем: H1, H2 –высоты точек А и В над эллипсоидом (нормальная высота плюс аномалия высоты); S – эллипсоидальное проложение измеренного расстояния d; с – хорда; b - центральный угол, стягивающий дугу S, для которой можно записать выражение
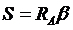
Из треугольника АВО имеем по теореме косинусов
(5. 7)
Здесь, как и при редуцировании базисных измерений, принята поверхность эллипсоида за поверхность шара радиусом нормального сечения эллипсоида, проходящего в азимуте А, вычисляемого по формуле Эйлера, рассмотренной в разделе сфероидической геодезии. Это существенно упрощает задачу и обеспечивает необходимую точность при расстояниях до 30 км. Учитывая это, из равнобедренного треугольника А0В0О имеем по теореме косинусов
(5. 8)
Подставляя выражение для cos b из в (5. 8), получаем после несложных преобразований выражение для длины хорды
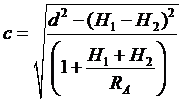(5. 9)
По теореме синусов имеем из треугольника А0В0О
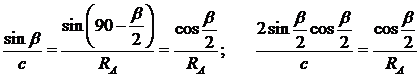
Разделив обе части полученного уравнения на cos b/2 ¹ 0, получаем для искомой величины S
(
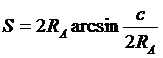Здесь возникает вполне уместный вопрос, почему нельзя воспользоваться более простым решением задачи, выразив из уравнения cosb, затем вычислив угол b по косинусу и подставив его значение в формулу Здесь проблема заключается в том, что значение угла b мало при малых, по сравнению с радиусом RA , расстояниях d и большим изменения искомого аргумента b соответствуют малые изменения косинуса. Вместе с тем, при малых значениях аргумента b изменения функции sinb практически линейно зависит от изменений аргумента. В этом преимущество вычислений по формуле
5. 4 Редуцирование горизонтальных направлений
Горизонтальные направления в геодезических построениях ( триангуляции и полигонометрии) измеряют теодолитами, главная ось которых ориентируется по отвесной линии. В этом случае коллимационная плоскость пересекает поверхность эллипсоида по прямому отвесному плоскому сечению и для перехода к прямому нормальному сечению необходимо ввести поправку за уклонение отвесной линии. Эта поправка аналогична поправке за уклонение отвесной линии при вычислении азимутов Лапласа и имеет выражение
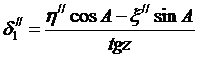
где h и x - составляющие уклонения отвеса в первом вертикале и меридиане соответственно для точки стояния теодолита; A и z – азимут и зенитное расстояние вдоль измеренного напрвления.
В государственных геодезических построениях значения зенитных расстояний близки к 900 , в этом случае даже при существенных значениях уклонений отвеса поправка мала. В условиях Республики Беларусь, когда местность равнинная и значения уклонений отвеса малы, эта поправка пренебрегаемо мала и ею можно пренебречь для любых классов геодезических построений. В Инструкции для построения государственных геодезических сетей СССР предусматривается учет этой поправки для тех направлений, когда зенитное расстояние отличается от 900 на величину более 20 (когда учитывают поправку за негоризонтальность алидады теодолита).
Центры геодезических пунктов государственных геодезических построений расположены на некоторой высоте над поверхностью эллипсоида. В этом случае имеем схему измерений, приведенную на рисунке 5. 5.
 |
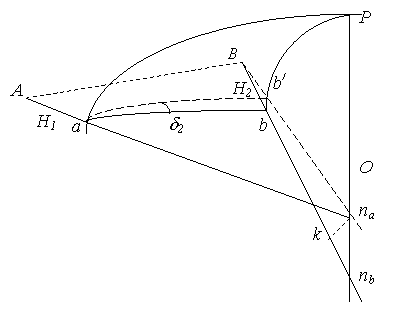Рис. 5. 5
Пусть геометрический центр теодолита находится в точке А на некоторой высоте над поверхностью эллипсоида Н1 (отрезок Аа), визирная цель В на некоторой высоте Н2 (отрезок Вb). О – центр эллипсоида. Нормали к поверхности эллипсоида в точках А и В пересекут его поверхность в точках а и b соответственно и не лежат в одной плоскости, поэтому они пересекут ось вращения эллипсоида в точках na и nb соответственно. Прямым нормальным сечением в точке А будет кривая ab эллипсоида. Коллимационная плоскость при этом пересечет поверхность эллипсоида по кривой ab/. Искомая поправка d2. Из рисунка можно заметить, что эта поправка зависит только от высоты визирной цели над поверхностью эллипсоида и не зависит от высоты точки А. Поэтому она носит название поправки за высоту наблюдаемого предмета.
Высота и расстояния между точками А и В малы по сравнению с радиусом Земли, поэтому можем с достаточной точностью положить линии bb/ и nak параллельными друг другу, а треугольник Abb/ плоским. Тогда можем записать
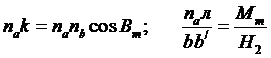
Отсюда получаем для bb/ выражение
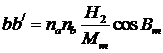
Из треугольника abb/ получаем по теореме синусов сферической тригонометрии
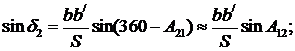
Разлагая sind в ряд, ограничиваясь первым членом разложения, получим
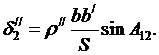
Отрезок nanb , как видно из рисунка 5. 5, получает выражение
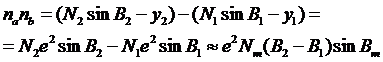
Здесь использовали известное выражение для ординаты точки на меридианном эллипсе 
, учитывая малые величины.
Из уравнения для малой дуги меридиана получаем приближенное выражение для разности широт
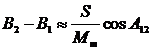
С учетом приведенных преобразований уравнение получает выражение для искомой поправки
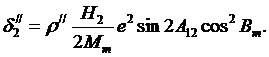
Для практики полезно заметить, что данную поправку необходимо учитывать в горных районах. В условиях Республики Беларусь, где высоты не превосходят величины в 400 м, величина этой поправки не превзойдет 0. 04// и ею можно пренебречь.
После учета поправок d1 и d2 в измеренных горизонтальных напрвлениях получаем на поверхности эллипсоида направления между прямыми нормальными сечениями. В треугольнике триангуляции в каждой вершине получают углы между взаимными нормальными сечениями. При этом получается фигура, не замкнутая измерениями, как это показано на рис.Здесь стрелками показаны направления прямых сечений.
 |
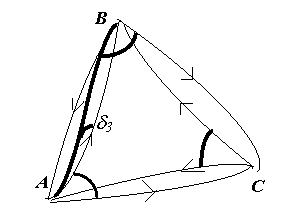Рис. 5. 6
Для того, чтобы получить фигуру в виде геодезического треугольника, сторонами которого являются геодезические линии, в горизонтальных направлениях при редуцировании на поверхность эллипсоида необходимо еще учитывать поправку d3 за переход от направления прямого нормального сечения к направлению геодезической линии.
Геодезическая линия проходит ближе к прямому в данной точке нормальному сечению, а угол между взаимными сечениями делится геодезической линией в отношении 1 : 2. Схема взаимного положения геодезической линии (утолщенная кривая) и нормальных сечений показана на рис. 5. 6 для точек А и В.
Формула для этой поправки получена известным немецким астрономо-геодезистом и имеет вид
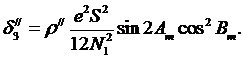
Несложно убедиться в том, что эта поправка незначительна и даже при расстояниях S = 50км не превышает величины, равной 0. 006//. Она учитывается только при работе в высокогорных районах, когда расстояния между пунктами превышает 50 км.
6. МЕТОДЫ ОПРЕДЕЛЕНИЯ КООРДИНАТНЫХ СИСТЕМ
6. 1. Общие сведения о методах градусных измерений
Как уже отмечалось ранее, в геодезии в качестве координатной принята поверхность эллипсоида вращения, параметры которого получены так, чтобы поверхность реальной Земли имела минимальные отступления от поверхности координатной. В этом случае редукционная проблема геодезии решается сравнительно просто рассмотренными ранее способами и редукционные поправки чаще всего пренебрегаемо малы.
Определение формы и размеров Земли, а также положения различных объектов на ней тесно связано с развитием и совершенствованием средств и методов измерений и составляют основную задачу геодезии. Эти основы были заложены в глубокой древности при решении задач познания окружающего мира, обеспечения навигации, а также при строительстве зданий, ирригационных, транспортных и иных сооружений. Так древнегреческий ученый Пифагор (около 571-497 гг. до н. э.) впервые предложил метод построения прямого угла на местности с помощью треугольника со сторонами в 3, 4 и 5 равных частей длины (теорема Пифагора ) и высказал предположение о шарообразности Земли. Эратосфен в Древнем Египте впервые (276-196 гг. до н. э.) определил радиус земного шара путем измерения длины дуги меридиана и разности широт (градусные измерения) между городами Александрия и Сиена. В Месопотамии (786-833 гг.) при халифе Аль-Мамуне арабскими учеными было получено значение радиуса земного шара, равное 6 406 км, точность которого была превзойдена только в XVII с применением метода триангуляции, предложенного в 1615 г. голландским ученым Снеллиусом ( гг.).
В предположении, что Земля – шар определенного радиуса, задача сводилась к определению из астрономических и геодезических измерений расстояния, соответствующего одному градусу дуги меридиана или параллели. Отсюда термин – градусные измерения методом дуг вдоль меридиана и параллели.
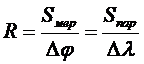
Здесь S мер и S пар – измеренные на местности расстояния вдоль меридиана или параллели соответственно, Dj и Dl - измеренные разности широт или долгот, R – искомый радиус Земли. Для однозначного определения радиуса необходимо выполнить градусные измерения вдоль одной дуги. При большем числе градусных измерений значение радиуса получали как среднее.
С развитием науки и техники совершенствовались приборы, технология измерений и их математическая обработка, накапливался объем информации, повышалась точность измерений. Так уже, начиная с XYII столетия, методом триангуляции стали определяться длины больших дуг меридианов и параллелей. Революционным шагом в развитии градусных измерений явилось введение международной единицы линейных измерений – метра, как 1 :части длины дуги Парижского меридиана. В результате определения и сравнения радиуса Земли, полученного учеными различных стран, обнаружили, что расхождения значений существенно больше, чем это может быть обусловлено ошибками измерений. Отсюда появилась гипотеза, что Земля не шар, а некоторое тело, поверхность которого ближе к поверхности эллипсоида вращения. На это указывал и закон Всемирного тяготения Ньютона, на основании которого в результате эволюции вращающийся земной шар должен принять форму эллипсоида вращения, сжатого у полюсов. Французские ученые по результатам обработки собственных градусных измерений пришли к выводу, что Земля – эллипсоид вращения, вытянутый у полюсов. Таким образом, теория Ньютона не подтвердилась. Это было вызвано тем, что дуги французских градусных измерений были небольшой длины и не могли описывать всю ее поверхность. Для устранения противоречия Французская академия наук организовала две международные экспедиции: Перуанскую ( 1735 – 1742 гг. ) и Лапландскую ( 1736 – 1737 гг. ). Перу расположено в экваториальной области, а Лапландия ( север современной Финляндии ) – с широтой около 660. Обработка результатов этих градусных измерений полностью подтвердили теорию Ньютона.
Для однозначного определения параметров эллипсоида: большой полуоси a и полярного сжатия a необходимо выполнить градусные измерения вдоль двух дуг. При большем числе дуг, значения параметров эллипсоида определяли по методу наименьших квадратов. При развитии метода триангуляции стало возможным получать градусные измерения из большого числа дуг меридианов и параллелей, связанных друг с другом общими вершинами. В этом случае дуги покрывали большие площади земной поверхности и параметры земного эллипсоида получали наиболее подходящими к данным площадям. В этом случае речь идет о методе площадей градусных измерений. Методы дуг и площадей основаны только на измерениях расстояний и углов ( разностей широт и долгот ), поэтому данные методы относят к геометрическим методам градусных измерений.
Если градусные измерения выполнены на всей поверхности Земли, получают параметры общего земного эллипсоида, центр которого совпадает с центром масс, а ось вращения с осью вращения Земли.
В том случае, когда необходимо подобрать положение эллипсоида так, чтобы его поверхность наилучшим образом подходила к части земной поверхности, например, для территории государства, поверхность эллипсоида ориентируют в теле Земли установлением исходных геодезических дат в некотором астрономо-геодезическом пункте, принятом за исходный для всей государственной геодезической сети. Исходные геодезические даты определяются из выражений:
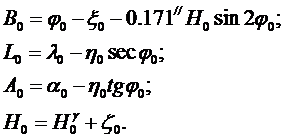(6.1)
В этом случае определяют параметры и ориентировку референц-эллипсоида. При этом параметры могут совпадать с параметрами общего земного эллипсоида, а ориентировка его в теле Земли такова, что ось вращения и плоскость экватора параллельны оси вращения и плоскости экватора общего земного эллипсоида.
Условия геометрической близости поверхности референц-эллипсоида к уровенной поверхности реальной Земли определяются уравнениями.
(6.2)
В том случае, когда речь идет о референц-эллипсоиде, условия (6.2) выполняются только для части поверхности Земли. Для общего земного эллипсоида – для всей ее поверхности. На практике обычно параметры определяют из градусных измерений, выполненных на всей поверхности Земли, а исходные геодезические даты для ориентировки референц-эллипсоида определяют из градусных измерений, выполненных на той территории, относительно которой определяют его ориентировку.
Для определения параметров земного эллипсоида, наряду с геометрическим, применяют физический метод, основанный на гравиметрических измерениях.
Геометрический метод имеет существенный недостаток, так как геодезические и астрономические измерения, в отличие от гравиметрических, могут быть выполнены только на суше, а на большей части земной поверхности, покрытой морями и океанами, такие измерения невозможны. Следует иметь в виду, что из гравиметрических измерений большая полуось определяется значительно грубее. Поэтому на практике применяют оба метода совместно. В этом случае большая полуось получается с погрешностью до 100 м, а полярное сжатие – до десятых долей знаменателя.
В последние десятилетия существенное развитие и практическое применение в геодезии находят методы, основанные на спутниковых системах позиционирования. Задача определения параметров земного эллипсоида в этом случае решается значительно оперативнее и точнее. Так, если для выполнения астрономо-геодезических и гравиметрических измерений на всей поверхности Земли потребовалось более 100 лет, то спутниковая информация и методы ее обработки сформированы за несколько десятилетий. При этом погрешность параметров земного эллипсоида характеризуется величинами: в большой полуоси 1 м, в полярном сжатии - сотые доли знаменателя.
6. 2. Уравнения градусных измерений по меридиану
Пусть имеется звено триангуляции АВ, вытянутое от исходного пункта А вдоль меридиана (рис. 6.1). В звене измерены углы треугольников, в пункте А установлены исходные геодезические даты. Производится уравнивание звена за все геометрические условия, кроме координатных (фигур, базисов, азимутов), а также решение треугольников. Последовательно решая прямую геодезическую задачу от пункта А, вычисляют геодезические коодинаты всех геодезических пунктов звена. Из решения обратной геодезической задачи между пунктами А и В получают длину диагонали звена D и ее прямой и обратный азимуты ТАВ и ТВА. Имея несколько таких звеньев, связанных общими пунктами, получаем картину (рис. 6.2). Естественно, из-за рельефа и других факторов, диагонали звеньев не будут совпадать с дугой меридиана. В этом случае проектируют по параллели точку В на меридиан точки А по формуле
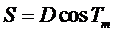
Здесь Tm – среднее значение из прямого и обратного азимутов звена. Погрешность, обусловленная кривизной поверхности эллипсоида, неучтенной в данной формуле, для длины звена в 250 км составит величину, менее 1 м.
Для вывода уравнения градусных измерений по меридиану достаточно использовать приближенную формулу для длины дуги меридиана
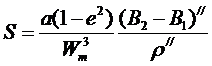(6.3)
Рис. 6. 1 Рис.6. 2
Целью градусных измерений является определение параметров эллипсоида, поэтому формулу (преобразуем, разлагая в ряд Wm-3 и ограничиваясь первым членом разложения, к виду
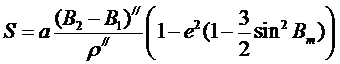(6.4)
Здесь геодезические широты двух точек отнесены к искомому эллипсоиду, параметры которого необходимо определить. Пусть будут известны некоторые приближенные параметры эллипсоида (например, из предыдущих определений), тогда искомые параметры выражаются как суммы приближенных параметров и некоторых поправок, определение которых производится из градусных измерений
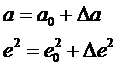(6.5)
При необходимости определения полярного сжатия, несложно перейти к нему от квадрата эксцентриситета по известной формуле.
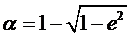
Подставляя выражения (в (, получим уравнение
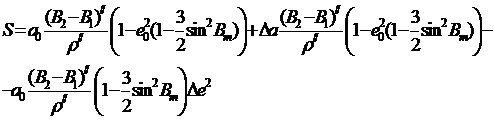(6.6)
Очевидно, первый член полученного уравнения выражает длину дуги меридиана на эллипсоиде с приближенными параметрами, радиус меридиана которого определяется выражением
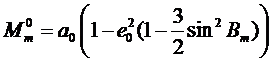(6.7)
Здесь различием геодезических широт средней точки на различных эллипсоидах, входящих в выражение с сомножителем e2, можно пренебречь. Разделив почленно уравнение (на (, получают
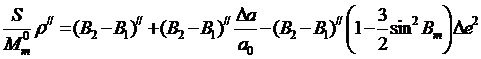(6.8)
Правая часть полученного выражения представляет собой ни что иное, как разность геодезических широт точек, расстояние между которыми S, на эллипсоиде с приближенными параметрами, следовательно, можем записать
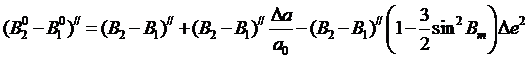(6.9)
Согласно первого уравнения (6.1) можем записать
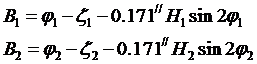
С учетом этого уравнение (6.9) может быть записано с принятой точностью
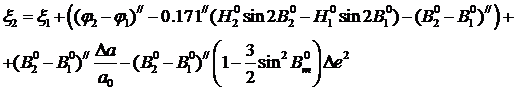(6.10)
Здесь геодезические широты и высоты вычислены относительно эллипсоида с приближенными параметрами. Введем обозначения:
, (
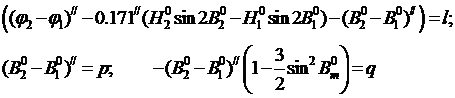Тогда уравнение (примет вид
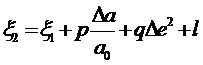
Если дуга градусного измерения состоит из n последовательных частных дуг, выходящих из начальной точки, то для каждой из них можем записать, условно придав некоторое значение для составляющей уклонения отвеса в начальной точке
(
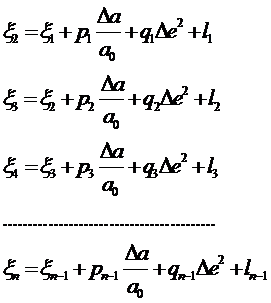Поверхность эллипсоида будет наилучшим образом подходить к уровенной поверхности Земли вдоль данного меридиана, если составляющие уклонений отвеса в меридиане будут малыми величинами и носить случайный характер. Выразим искомые значения составляющих уклонений отвеса xi ( i = 2, 3,…n ) через составляющую уклонения отвеса в начальной точке x1. Для этого уравнения (запишем в виде
(
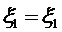
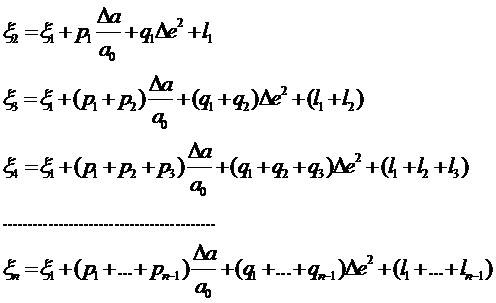Введя обозначения:
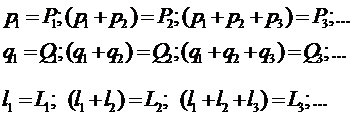
Получим уравнения (в виде
(
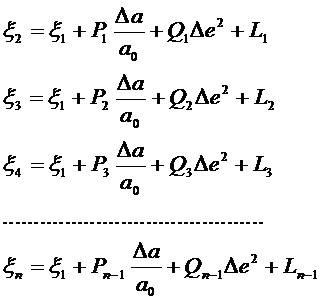Уравнения (можно рассматривать как параметрические уравнения поправок, в которых роль искомых параметров будут играть составляющая уклонения отвеса в начальном пункте x1, а также поправки к приближенным параметрам эллипсоида Da и De2 . Для однозначного решения задачи необходимо иметь три дуги. При n > 3 данную систему уравнений решают под условием
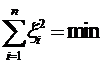
Таким образом, задача сводится к решению системы уравнений (под условием (, что приводит к решению трех нормальных уравнений с тремя неизвестными параметрми.
(
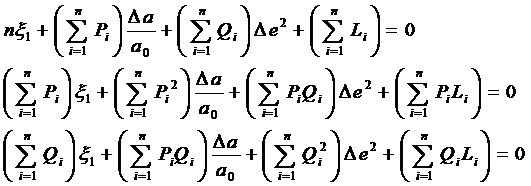Уравнения (представляют собой уравнения градусных измерений по меридиану, полученные методом развертывания. Это объясняется тем, что в свободном члене уравнения (величина ( B20 - B10 ) вычисляется по расстоянию S, редуцированному на уровенную поверхность ( геоид ), а не на поверхность эллипсоида.
6. 3. Уравнения градусных измерений по параллели
Пусть в звене триангуляции 1 класса, вытянутого вдоль параллели (рис. 6. 3), аналогично тому, как это рассмотрено в предыдущем случае, вычислена длина диагонали D, ее прямой и обратный азимуты. Не представляет труда вычислить длину дуги параллели Sk на средней широте точек А и В.
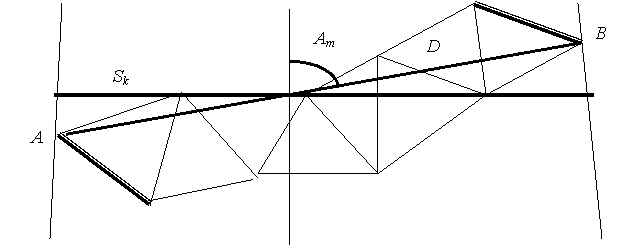
Имея несколько последовательных звеньев, связанных общими пунктами Лапласа, получают картину ( рис.
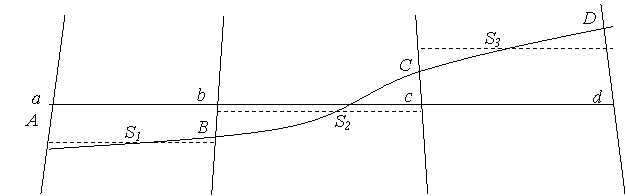
Рис. 6. 4
Здесь проекции диагоналей звеньев Si представляют собой длины дуг параллелей на средней широте соответствующей диагонали. Для вычисления длины дуги параллели между точками a и b находят отрезки дуги параллели Si0 на средней широте всех звеньев ( точек A и D ), участвующих в градусном измерении, из соотношения
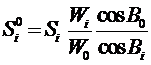
Таким образом, имеют уравнение длины дуги параллели ab
(
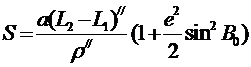Вводя обозначения (, а также учитывая уравнения исходных геодезических дат для долготы
(
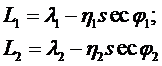получаем аналогично тому, как это сделано в выводе уравнений по меридиану, параметрические уравнения
(
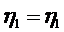
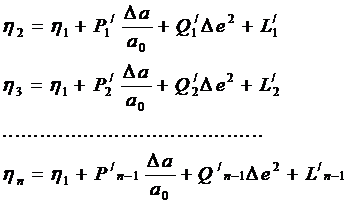Решая систему (под условием
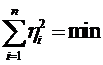
получают нормальные уравнения вида, аналогичного (
На практике системы (и (решают совместно под условием
(
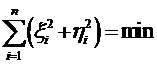В результате получают поправки к приближенным параметрам эллипсоида и составляющие уклонений отвеса в исходном пункте при условии их наилучшего соответствия дугам меридианов и параллелей, участвующих а градусных измерениях.
6. 4. Уравнения градусных измерений по методу площадей
Рассмотренные методы градусных измерений применялись, когда в них участвовали разрозненные дуги. При реализации программы построения государственной геодезической сети 1 класса в СССР диагонали звеньев позволяли формировать взаимосвязанные дуги меридианов и параллелей, покрывающие огромные площади земной поверхности. В этом случае целесообразнее искать параметры эллипсоида и составляющие уклонений отвеса в исходном пункте так, чтобы его ориентировка и параметры наилучшим образом подходили к площади уровенной поверхности Земли. В этом случае говорят о градусных измерениях по методу площадей. Кроме того, здесь возможно применение строгого метода проектирования, в отличие от метода развертывания, рассмотренного выше.
В данном случае имеется некоторый референц-эллипсоид с параметрами a0 a0, ориентировкой, определяемой исходными геодезическими датами B0, L0,, A0, z0. В России и затем в Советском Союзе до 1946 года применялся референц-эллипсоид Бесселя с исходными геодезическими датами, установленными для центра главного пункта Пулковской астрономической абсерватории. В принципе эти параметры и исходные даты можно получить, применяя рассмотренные выше способы градусных измерений по методу развертывания.
Таким образом, имеют некоторые ранее принятые параметры и ориентировку референц-эллипсоида: a0, a0, B0,, L0,, A0,,z0. Необходимо определить из градусных измерений, выполненных на территории государства, поправки к ранее принятым параметрам, а также уточнить ориентировку референц-эллипсоида. Следует заметить, что параметры общего земного эллипсоида могут быть определены только из обработки мировых градусных измерений.
Координаты в исходном геодезическом пункте государства определяются выражениями (, которые можем записать в виде:
(
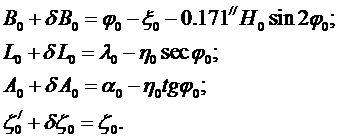Для произвольного астрономо-геодезического пункта сети будем иметь для геодезических координат на искомом эллипсоиде ( широт, долгот, азимутов и аномалий высот ):
(
|
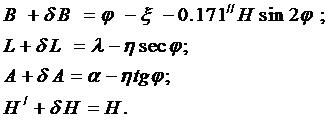Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 |
