Изгиб пластинок (стр. 1 )

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ПУТЕЙ СООБЩЕНИЯ

Кафедра «Прочность материалов и конструкций»

,

Изгиб пластинок

Учебное пособие

Санкт-Петербург

2011

УДК 624.073

С50

Р е ц е н з е н т ы:

доктор технических наук, профессор кафедры

«Сопротивление материалов и теория упругости»

ФГБОУ ВПО ПИМаш (ЛМЗ-ВТУЗ)

;

кандидат технических наук, доцент кафедры

«Прочность материалов и конструкций»

ФГБОУ ВПО ПГУПС

,

Изгиб пластинок: учеб. пособие / , . – СПб.: Петербургский гос. ун-т путей сообщения, 2011. – 51 с.

Приведены основы теории и примеры решения задач по изгибу эллиптических, круглых и прямоугольных пластин. При этом используются как классические аналитические методы решения указанных задач, так и аналитические методы, основанные на применении математического аппарата разрывных функций.

Предназначено для аудиторной и самостоятельной работы студентов всех форм обучения.

УДК 624.073

© Петербургский государственный

университет путей сообщения, 2011

© , , 2011

Введение

В соответствии с принятым ФГОС ВПО (2011 г.) по дисциплинам сопротивление материалов, строительная механика сокращается количество часов аудиторных занятий и увеличивается время, отводимое на самостоятельную работу студентов. В связи с этим появилась необходимость в дополнительных методических материалах, позволяющих познакомиться с современными аналитическими методами расчëтов таких элементов конструкций, как пластинки.

Данное учебное пособие состоит из двух глав.

В первой главе приведены основы теории и примеры решения задач по изгибу эллиптических, круглых и прямоугольных пластин. Примеры сопровождаются теоретической и методической информацией по решению задач. Кроме того, по каждой теме приведены расчëтно-проектировочные задания для самостоятельного решения. Задачи составлены с большим числом вариантов, что обеспечивает индивидуальность исходных данных.

Во второй главе на основе математического аппарата обобщëнных функций излагается в доступной форме эффективный аналитический метод расчëта пластин на действие статических нагрузок. Рассматриваются круглые пластинки под действием равномерно распределëнной нагрузки, как по всей еë поверхности, так и кольцевой поверхности при различных условиях закрепления пластинки.

Учебное пособие предназначено для аудиторной, самостоятельной и научно-исследовательской работы студентов, изучающих сопротивление материалов и строительную механику. Рекомендуется для подготовки к самостоятельному решению задач, выполнению расчëтно-проектировочных заданий, к контрольным работам, зачетам и экзаменам в качестве дополнения к теоретическому курсу сопротивления материалов и строительной механики. Оно может быть полезно магистрам, аспирантам и стажерам.

Глава 1. Изгиб тонких пластинок

1.1 Основные понятия и гипотезы

Пластины являются одним из основных конструктивных элементов многих инженерных сооружений. Под пластиной понимается тело, у которого одно измерение (высота, толщина) мало по сравнению с двумя другими размерами.

Высота (толщина) пластины может быть переменной, при пластина называется пластиной постоянной толщины. Далее рассматриваются именно такие пластины. Плоскость, разделяющая пополам толщину пластины, называется срединной плоскостью. При изгибе пластины она превращается в срединную поверхность. Контуром пластины называют линию, ограничивающую срединную плоскость пластины.

В прямоугольной системе координат оси и будем располагать в срединной плоскости пластины, а ось – направлять вниз (рис. 1.1). Перемещения срединной поверхности в направлении оси называют прогибом пластины и обозначают .

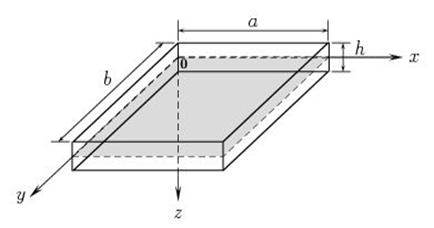
Рис. 1.1. Пластинка: срединный слой и размеры

В зависимости от соотношения наименьшего размера основания и толщины различают три вида пластин:

• при 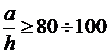пластины относят к мембранам; мембраны обладают незначительной изгибной жëсткостью и работают в основном на растяжение;

• при пластина считается толстой и часто называется плитой: расчëт плит ведëтся как для массивных трëхмерных тел;

• при 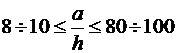пластины называют тонкими; такой тип пластин чаще всего встречается для в инженерных приложениях. Их расчëт ведëтся с некоторыми упрощающими предположениями.

В зависимости от способности деформироваться тонкие пластины делятся на жëсткие и гибкие.

Если наибольший относительный прогиб при изгибе , то пластина считается жëсткой и напряжениями растяжения (сжатия), возникающими в еë срединной плоскости пренебрегают. Если величина превышает указанные пределы, то пластину считают гибкой, она работает одновременно и на изгиб и на растяжение (сжатие), то есть как мембрана.

Далее рассматриваются тонкие жëсткие пластинки, работающие на изгиб. Сформулируем некоторые допущения и ограничения (гипотезы), благодаря которым расчëт тонких пластин упрощается и сводится к решению линейных дифференциальных уравнений.

1. Основная гипотеза о прямых нормалях: прямолинейные отрезки, нормальные (перпендикулярные) к срединной плоскости пластины до деформации, остаются такими же и после деформации. Эта гипотеза аналогична гипотезе плоских сечений (гипотезе Бернулли), принимаемая в сопротивлении материалов при расчëте стержней.

2. Гипотеза об отсутствии поперечного давления: слои пластины, параллельные срединной плоскости, не давят друг на друга и поэтому соответствующими нормальными напряжениями сжатия , которые значительно меньше и можно пренебречь.

Эти два допущения часто называют гипотезами Кирхгофа.

3. Гипотеза о вертикальном смещении точек срединной поверхности: точки срединной поверхности смещаются только в перпендикулярных к ней направлениях, то есть по направлению оси . Горизонтальными перемещениями срединной плоскости 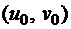в силу их малости пренебрегают.

Вследствие принятых допущений решение задачи по определению напряжëнно-деформированного состояния (НДС), то есть по определению внутренних усилий, напряжений и перемещений в сечении пластины значительно упрощается. Задача решается в перемещениях и за основную искомую функцию принимается прогиб 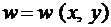, то есть вертикальное перемещение.

1.2 Перемещения и деформации в пластине

Будем рассматривать пластинки постоянной толщины, нагруженные поперечной распределëнной нагрузкой , которую для краткости далее обозначаем просто . Под действием этой нагрузки пластинка прогибается и срединный слой, искривляясь, образует поверхность .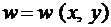

Горизонтальные перемещения точек пластины, не принадлежащие срединной плоскости, в направлении осей и условимся обозначать и соответственно. Углы поворота нормали к срединной плоскости по отношению к осям и (рис. 1.2) будут

, .

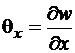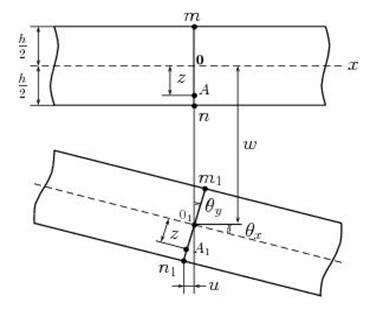
Рис. 1.2. Горизонтальное перемещение

Из рис. 1.2 видно, что перемещение , а, следовательно, и перемещение , определятся так

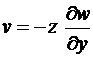, . (1.1)

Используя соотношения Коши, связывающие линейные деформации , , угловые деформации и перемещения и следующим образом:

, , ,

получим выражения для деформаций в пластинке

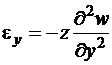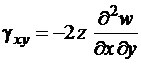, , , (1.2)

.

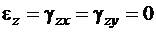Знак минус означает, что перемещение точки при происходит в сторону, противоположную направлениям осей и .

1.3 Напряжения и внутренние усилия в пластине

Согласно закону Гука (с учëтом принятого допущения )

,

,

,

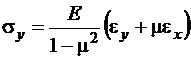где модуль Юнга, коэффициент Пуассона материала пластинки. Подставив сюда выражения (1.2), получим

,

,

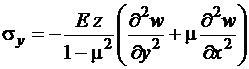. (1.3)

Из выражений (1.3) следует, что напряжения , и зависят от координаты линейно. Можно получить выражения для компонент и , но они здесь не понадобятся.

В соответствии с условиями статической эквивалентности внутренние моменты, возникающие в пластине, определяются следующими выражениями:

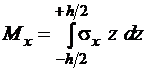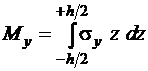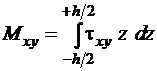, , . (1.4)

Подставляя формулы для напряжений (1.3) в соотношения (1.4), получим значения моментов, выраженные через прогиб пластинки

,

,

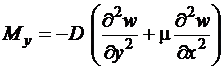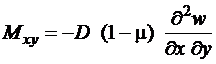. (1.5)

Здесь , изгибающие моменты, – крутящие моменты. Величина

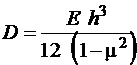(1.6)

называется цилиндрической жëсткостью и является физико-геометрической характеристикой пластинки при изгибе. Цилиндрическая жëсткость пластины при изгибе отличается от обычной изгибной жëсткости балки множителем , который учитывает увеличение жëсткости пластинки благодаря возникновению плоского напряжëнного состояния при цилиндрическом изгибе в отличие от линейного напряжëнного состояния волокон обычной балки. Указанное увеличения жëсткости составляет около .

Поперечные силы выражаются через моменты следующими уравнениями

, .

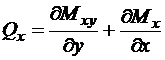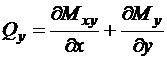Подставляя сюда соотношения (5), получаем значения поперечных сил в зависимости от прогиба пластины

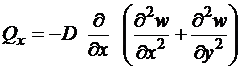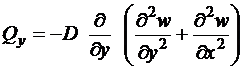, . (1.7)

Отметим особенности обозначения внутренних силовых факторов в пластинах, отличные от тех, что были приняты в балках:

– изгибающий момент относительно оси, перпендикулярный к ; – изгибающий момент относительно оси, перпендикулярный к , – крутящий момент относительно оси , действующий в плоскости, параллельной оси ; – крутящий момент относительно оси , действующий в плоскости, параллельной оси (рис. 1.3).

Различие между поперечными силами и состоит в том, что первая действует на площадке с нормалью, параллельной оси , а вторая – на площадке с нормалью, параллельной оси .

Кроме того, следует принять во внимание, что изгибающие и крутящие моменты, а также поперечные силы отнесены к единице длины сечений, параллельных плоскостям и (рис. 1.1).

Рис. 1.3. Напряжения и внутренние усилия в пластине

1.4 Дифференциальное уравнение изгиба пластины

Если выделить в пластинке элементарный параллелепипед и спроектировать все силы, действующие на него, на ось , то из условия равновесия можно получить следующее тождество (выкладки опускаем)

,

где поперечная нагрузка.

Подставляя сюда выражения для поперечных сил (1.7), получим дифференциальное уравнение пластины

. (1.8)

Уравнение (1.8) называют уравнением Софии Жермен и записывают короче так:

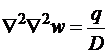или , (1.9)

где – гармонический дифференциальный оператор ( набла) в декартовых координатах (оператор Лапласа).

Расчëт пластинок сводится к интегрированию уравнения (1.9) при заданной правой части (нагрузке) и определëнных граничных условиях.

1.5 Граничные условия

Задача интегрирования уравнения (1.9) заключается не только в том, чтобы найти функцию 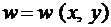, подстановка которой в дифференциальное уравнение (1.9) удовлетворяла бы последнее уравнение тождественно, но так же и в том, чтобы эта функция удовлетворяла условиям на опорном контуре. Наиболее часто встречающимися вариантами закрепления контура пластинки являются следующие (на примере прямоугольной пластины, рис. 1.1):

1) З а щ е м л ë н н ы й к р а й.

Защемление боковой грани пластинки (при ) означает отсутствие любых смещений, – горизонтальных, вертикальных и угловых, а значит, и углов поворота . Поэтому

(1.10)

2) Ш а р н и р н о – о п ë р т ы й к р а й.

Шарнирно-опëртая грань пластины не смещается в вертикальной плоскости, но может перемещаться в горизонтальной и поворачиваться. Это означает отсутствие прогиба и изгибающего момента на этой грани:

.

В силу первого равенства, на всëм контуре обращается в нуль также и производные, поэтому граничные условия упрощаются и для шарнирно-опëртого края будут

(1.11)

3) С в о б о д н ы й к р а й (отсутствие опорных связей).

Кирхгофом было показано, что для определения прогиба , удовлетворяющего уравнению (8), достаточно два условия на свободной грани :

, . (1.12)

Если на свободном крае пластинки приложены внешний изгибающий момент или распределëнная нагрузка , то в правые части равенств (1.12) надо подставить соответственно и .

В случае пластины с криволинейным контуром вводится система координат, связанная с нормалью и касательной к контуру пластины, и граничные условия переписываются через прежние прямоугольные координаты.

Ниже рассматриваются эллиптические пластинки с первым граничным условием, то есть жëсткой заделкой и круглые пластики с различными закреплениями.

1.6 Эллиптическая пластинка

Рассмотрим эллиптическую пластинку, защемлëнную по контуру и нагруженную равномерно распределëнной нагрузкой интенсивности (рис. 1.4). Оси и выберем так, чтобы они проходили через центр пластинки. Тогда уравнение контура

,

где и – большая и малая полуоси эллипса. Граничным условиям (1.10) будет удовлетворять функция (прогиб)

. (1.13)

Это выражение и его первые производные по и обращаются на контуре в нуль. При выражение превращается в , что является прогибом в центре пластинки. Эту величину найдем, подставив решение (1.13) в уравнение (1.8).

После дифференцирования находим

. (1.14)

Выражения для изгибающих моментов , и крутящего момента найдëм, подставив выражение для прогиба (1.13) в формулы 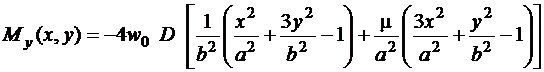(1.5):

;

;

. (1.15)

Выделим значения моментов в характерных точках:

– на концах большой полуоси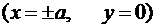

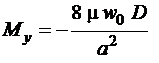, , ; (1.16)

– на концах малой полуоси

, , ; (1.17)

– в центре пластинки

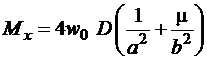, , . (1.18)

Так как зависимость изгибающих моментов от координат имеет вид параболической функции, то для построения эпюр и необходимо взять минимум три точки.

Аналогичным образом найдëм выражения для поперечных сил вдоль координатных осей, подставив функцию прогиба (1.13) в формулы (1.7):

,

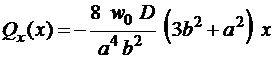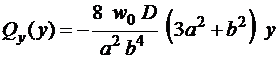. (1.19)

В центре пластинки всегда .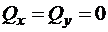

Наконец, подставляя из выражения (1.13) в формулы (1.3), вычислим напряжения в пластине:

;

;

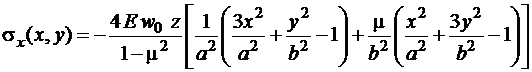. (1.20)

Напряжения в центре пластинки

,

,

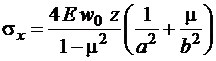. (1.21)

Пример расчëта. Рассмотрим эллиптическую пластинку, защемлëнную по контуру и нагруженную равномерно распределëнным давлением интенсивности .

Дано: давление , размер пластины , , толщина , коэффициент Пуассона , модуль упругости , допускаемое напряжение на сдвиг (материал – сталь).

Требуется:

1. Определить наибольший прогиб пластины (в еë середине).

2. Построить эпюры поперечных сил и изгибающих моментов по направлению главных диаметров контура.

3. В точке с координатами определить главные напряжения и выполнить проверку на прочность по III теории: .

Р Е Ш Е Н И Е

Жëсткость заданной пластинки, согласно выражению (1.6)

.

1) Прогиб в центре пластины (формула (1.14))

.

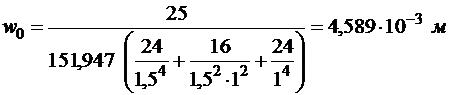2) Величины поперечных сил вдоль главных диаметров, совпадающих с направлениями координатных осей, определяем по формулам (1.19), а величины изгибающих моментов – по формулам (1.15), полагая для , а для .

Результаты вычислений с шагом сводим в табл. 1.1.

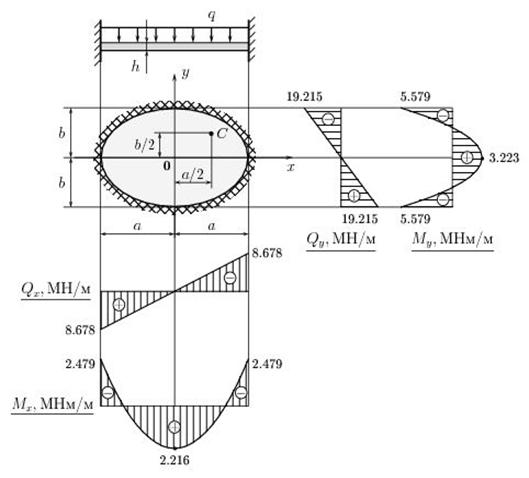
Эпюры внутренних усили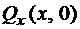й , , и приведены на рис. 1.4.

Т а б л и ц а 1.1

Величины поперечных сил и изгибающих моментов, возникающих в эллиптической пластине

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5