Изгиб пластинок (стр. 2 )

Рис. 1.4. Эпюры внутренних усилий в эллиптической пластинке

3) Главные напряжения при плоском напряженном состоянии определяются по формуле

, (1.22)

где , .

Для точки 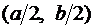выражения

и

обращаются в нуль. Поэтому, согласно выражениям (1.20), нормальные напряжения в точке отсутствуют , то есть материал в данной точке находится в состоянии чистого сдвига. Следовательно,

.

Окончательно индексацию главных напряжений производим с учëтом условия :

, , .

Определяем максимальное касательное напряжение по формуле

,

откуда получаем

.

Наибольшее касательное напряжение в эллиптической пластине возникает на еë поверхности .

Подставляя исходные данные в третью формулу (1.20) при

, , ,

находим: .

Таким образом, прочность пластины в точке не обеспечивается. Необходимо либо уменьшить нагрузку, либо увеличить размеры пластины, или и то и другое одновременно.

1.7 Круглая пластинка

При определении напряжëнно-деформированного состояния (НДС) круглых пластин удобно пользоваться полярными координатами , которые связаны с прямоугольными следующими соотношениями:

, , , ,

а вторая производная по координате преобразуется следующим образом:

.

Дифференциальное уравнение изгиба круглой пластинки (1.9) запишем в виде

. (1.23)

Поскольку круглая пластинка замкнута в окружном направлении, то в силу периодичности по углу всех функций, определяющих НДС пластинки, еë прогиб можно представить в такой форме:

,

где параметр, определяющий тип деформации ( соответствует осесимметричной деформации; – соответствует кососимметричной деформации; – соответствует циклически симметричным деформациям). Таким образом, в исходном расчëтном дифференциальном уравнении (1.23) можно избавиться от производных по окружной координате .

В случае осесимметричного нагружения пластинки (далее рассматриваются только такие задачи) равномерно распределëнной нагрузкой , что соответствует осесимметричной деформации пластинки, это уравнение принимает вид

. (1.24)

Вид решения уравнения (1.24) зависит от условия закрепления пластинки. Как и в случае эллиптической пластинки, здесь так же будем рассматривать вариант заделки (жëсткое защемление) контура ( – радиус пластинки):

В этом случае (, край пластинки заделан) решением уравнения (1.24) будет

, (1.25)

что легко проверить непосредственной подстановкой в соотношение (1.24).

Угол поворота сечения

. (1.26)

Внутренние усилия в пластинке в случае осевой симметрии выражаются через прогиб следующим образом:

,

,

,

где и – изгибающие моменты, возникающие в радиальном и в окружном направлениях пластинки соответственно, – радиальная перерезывающая сила.

Подставляя сюда значения (1.25), получаем

,

,

. (1.27)

В центре пластинки

, (1.28)

на контуре

, . (1.29)

Нормальные напряжения в пластинке вычисляются по формулам:

,

,

где , – радиальное и окружное напряжения.

Подставляя сюда функцию прогиба (1.25), получаем

,

. (1.30)

В центре пластинки

, (1.31)

на контуре

, . (1.32)

Пример расчëта. Рассмотрим круглую пластинку радиуса , защемлëнную по контуру и нагруженную равномерно распределëнным давлением интенсивности .

Дано: давление , радиус пластины , коэффициент Пуассона , модуль упругости , допускаемое нормальное напряжение (материал – сталь).

Требуется:

1. Построить эпюры изгибающих моментов в радиальном и окружном направлениях и .

2. Определить необходимую толщину пластины.

3. Вычислить максимальный прогиб пластины.

Р Е Ш Е Н И Е

1) Эпюры радиального и окружного изгибающих моментов определены по формулам (1.27) и приведены на рис. 1.5.

2) Условие прочности по третьей теории

. (1.33)

Нормальные напряжения являются главными, однако согласно принятому допущению напряжение (напряжëнное состояние плоское). Поэтому, с учëтом правила индексации главных напряжений

,

принимаем в соответствии с формулой (32):

, .

Разность достигает максимума на контуре пластинки , в то время как в центре пластинки она равна нулю (формула (1.31)). Таким образом, опасная точка будет возле заделки .

Рис. 1.5. Эпюры изгибающих моментов в круглой пластинке

Принимая в этой точке , то есть верхнюю грань пластинки, по формулам (1.31) имеем

,

откуда находим необходимую толщину пластинки

.

3) Определим максимальный прогиб пластины.

Согласно уравнению (1.25) он достигается в центре пластины . Предварительно находим цилиндрическую жëсткость по формуле (1.6)

.

Тогда

. (1.34)

1.8 Прямоугольная пластинка

Для прямоугольной пластинки, все грани которой являются шарнирно опëртыми, решение уравнения (1.8), предложенное Л. Надаи, можно представить в виде двойного тригонометрического ряда

, (1.35)

где и – стороны прямоугольной пластины (рис. 1); – коэффициенты разложения прогиба в двойной ряд Фурье, подлежащие определению (постоянные числа); и – целые положительные числа:

Внешняя поверхностная нагрузка также раскладывается в двойной тригонометрический ряд

, (1.36)

где коэффициенты разложения определяются из выражения

. (1.37)

Если соотношения (1.35) и (1.36) подставить в уравнение (1.8), приравнять соответствующие коэффициенты и решить полученное равенство, то получим

; . (1.38)

Определив коэффициенты по формуле (1.38) и прогиб пластины по формуле (1.35), можно найти внутренние усилия по формулам (1.5) – (1.7). Для равномерно распределëнной нагрузки имеем:

– прогиб пластинки

; (1.39)

– прогиб в центре (максимальный)

; (1.40)

– изгибающие моменты

,

; (1.41)

– крутящий момент

; (1.42)

– поперечные силы

,

; (1.43)

– нормальные напряжения

, ; (1.44)

– касательные напряжения

, , . (1.45)

В формулах (1.38) – (1.45) и ; ; – погонный момент инерции, имеющий размерность метр в кубе. Моменты , , имеют размерность силы, ; размерность , – сила, отнесëнная к единице длины (погонная поперечная сила), . Статические моменты площади и относительно осей и берутся для той части сечения пластинки, которая расположена выше горизонта, на уровне которого вычисляются касательные напряжения так же. Эти величины также отнесены к единице длины.

Пример расчëта. Требуется определить необходимую толщину пластинки размером , , нагруженную равномерно распределëнной нагрузкой . Материал пластины – сталь с механическими свойствами: коэффициент Пуассона ; допускаемое напряжение .

Расчëт выполнить для центра пластинки .

Использовать первую теорию прочности:

.

Р Е Ш Е Н И Е

В центре пластинки , а выражения для изгибающих моментов принимают вид

, (1.46)

. (1.47)

Подставляя значения, вычисленные по формулам (1.46) и (1.47), последовательно в выражения (1.44) и (1.22) можно получить, что толщина пластины определяется из условия:

. (1.48)

Таким образом, необходимо вычислить изгибающие моменты по формулам (1.46) и (1.47). Ограничимся первыми тремя членами ряда, то есть (чем больше членов ряда, тем выше точность).

Предварительно вычислим коэффициенты

, .

Далее, последовательно находим

•  при

,

,

•  при

,

,

•  при

,

,

•  при

,

,

•  при

,

,

•  при

,

,

•  при

,

,

•  при

,

,

•  при

,

.

Суммируем полученные значения:

,

.

Вычисляем толщину пластины

,

.

Так как , то минимально допустимая толщина пластины

.

1.9 Задачи для расчëтно-проектировочных работ

При подготовке к выполнению расчëтно-проектировочных работ рекомендуется предварительно изучить разделы теории, относящиеся к теме задания. Расчëты ведутся сначала в обычном (буквенном) виде, затем в числа. Схемы и эпюры выполняются карандашом с обязательным соблюдением масштаба. Работа оформляется на листах формата А4 с титульным листом, исходными данными, заголовками к каждому этапу решения.

1.9.1 Изгиб эллиптической пластинки

Для эллиптической пластинки постоянной толщины , жëстко заделанной по контуру и нагруженной равномерно распределëнной нагрузкой , необходимо:

1. Определить наибольший прогиб пластины (в еë середине).

2. Построить эпюры поперечных сил и изгибающих моментов по направлению главных диаметров контура.

3. В точке с координатами определить главные напряжения и выполнить проверку на прочность по III теории: .

Исходные данные взять из табл. 1.2.

Для стальной пластины принять: , , .

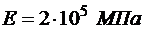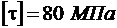Для пластины из бетона: , , .

1.9.2 Изгиб круглой пластинки

Для круглой пластинки заданного радиуса , жëстко заделанной по контуру и нагруженной равномерно распределëнной нагрузкой , необходимо:

1. Построить эпюры изгибающих моментов и по направлению диаметра пластины.

2. Определить необходимую толщину пластины.

3. Вычислить максимальный прогиб пластины.

Значения и принять по формулам: ; , где – номер варианта. Принять , , (сталь).

1.9.3 Изгиб прямоугольной пластинки

Определить необходимую толщину прямоугольной, шарнирно опëртой по всем граням пластинки, размером и нагруженной равномерно распределëнной нагрузкой . Расчëт выполнить по первой теории прочности. Исходные данные взять из табл. 1.3.

Т а б л и ц а 1.2

Исходные данные для расчëта эллиптической пластинки

Т а б л и ц а 1.3

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5