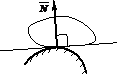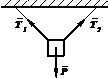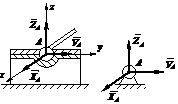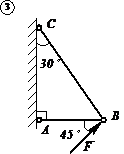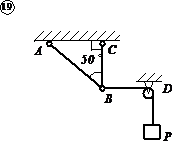Техническая механика. Статика и кинематика (стр. 1 )

Волгоград

2009

УДК

Т 38

Рецензенты: к. т. н., генеральный директор Ротор» ; преподаватель высшей квалификационной категории Камышинского технического колледжа .

Корзун, механика. Статика и кинематика: учеб. пособие / , , ; Волгоград. гос. техн. ун-т. – Волгоград, 2009. – 72 с.

ISBN 0177-2

Разработано в соответствии с рабочей программой по дисциплине «Техническая механика».

Содержится краткая теория по основным вопросам, необходимый для выполнения практических заданий материал, примеры выполнения заданий и контрольные вопросы по 2-м разделам: «Статика» и «Кинематика». Предназначено для студентов СПО, обучающихся по специальностям 151001.51 «Технология машиностроения», 260704.51 «Технология текстильных изделий», 140212.51 «Электроснабжение».

Ил. 32. Табл. 12. Библиогр. 5 назв.

Печатается по решению редакционно-издательского совета

Волгоградского государственного технического университета

ISBN 0177-2 Ó Волгоградский

государственный

технический

университет, 2009

ВВЕДЕНИЕ

Цель данного пособия – обратить внимание студентов на те основополагающие понятия, которые используются при решении задач по первой части дисциплин «Техническая механика» «Теоретическая механика», а также способствовать индивидуализации обучения.

Краткое, дозированное изложение теоретических положений по отдельным темам, подробные пояснения к примерам решения задач и контрольные вопросы позволят более полно организовать самостоятельную работу, как на практических занятиях, так и во внеаудиторное время.

Требования к оформлению задания

1.  Работа выполняется на листах бумаги стандартного формата

А4 (210´297) мм.

2.  Все схемы и рисунки выполняются в карандаше с помощью инструментов (циркуль, линейка, транспортир) точно, аккуратно и четко подписываются.

3.  Последовательность оформления: тема задания; условие задачи; схема; решение (с подробными пояснениями); ответ.

Последовательность выполнения

○  Изучить теоретический материал.

○  Ответить на контрольные вопросы.

○  Разобрать самостоятельно предложенные номера задач.

РАЗДЕЛ I «Статика»

Практическое занятие № 1

Тема: Определение реакций связей в плоской сходящейся системе сил.

Цель: Освоить определение реакций связей в случае действия на тело плоской сходящейся системы сил.

Время проведения: 2 часа.

1. Основные положения теории

1.1. Понятие об абсолютно твердом теле и материальной точке

Объектом изучения в теоретической механике является абсолютно твердое тело. Это материальное тело, в котором расстояние между любы-

ми двумя его точками остается неизменным при действии на него сил.

Материальной точкой называют абсолютно твердое тело, размерами которого можно пренебречь в условии данной задачи.

1.2. Понятие о силе

Мера механического взаимодействия двух тел называется силой.

Сила – величина векторная, характеризуется тремя элементами:

○  величиной (модулем);

○  точкой приложения;

○  направлением.

По способу задания различают силы активные (заданные или известные) и реактивные (неизвестные).

1.3. Связи и их реакции

○  При решении задач по статике, относящихся к равновесию твердого тела, почти всегда рассматриваемое тело является несвободным, т. е. таким, которое соприкасается или скреплено с другими телами, благодаря чему становятся невозможными те или иные перемещения данного тела.

○  Тела, ограничивающие свободу перемещения данного тела, называются наложенными на него связями.

○  Сила, с которой связь действует на тело, препятствуя его перемещению в том или ином направлении, называется реакцией связи.

Реакция связи приложена к твердому телу в точке их касания и направлена в сторону, противоположную тому направлению, в котором связь препятствует перемещению данного тела.

1.4. Основные типы связей

1.  Гладкая опорная поверхность (рис.1, а, б, в).

Реакция направлена по общей нормали к соприкасающимся поверхностям (см. рис. 1 а).

Реакция направлена перпендикулярно к балке АВ и проходит через точку соприкосновения связи и тела. направлена перпендикулярно опорной поверхности (см. рис. 1, б).

Разновидностью гладкой опорной поверхности является опора на катках – шарнирно-подвижная опора.

Ее реакция направлена перпендикулярно опорной поверхности и приложена в центре шарнира (см. рис. 1, в).

1.5. Понятие о проекции силы на ось

Проекцией вектора силы на ось называется отрезок оси, заключенный между основаниями перпендикуляров, опущенных из начала и конца вектора на эту ось (рис. 8).

Проекция силы на ось равна произведению модуля этой силы на косинус острого угла между направлением силы и направлением оси.

Проекция силы на ось считается положительной, если между направлением вектора силы и положительным направлением оси угол

острый и отрицательной – если тупой (см. рис. 8, а, б).

Проекция силы на ось равна модулю силы, если вектор силы направлен параллельно оси, или лежит на этой оси (см. рис. 8, в, г).

Проекция силы на ось равна нулю, если вектор силы расположен перпендикулярно этой оси (см. рис. 8, д).

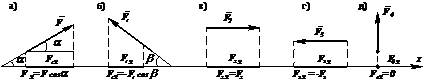
Рис. 8.

1.6. Равновесие плоской системы сходящихся сил

Плоской сходящейся называется система сил, линии действия которых расположены в одной плоскости и пересекаются в одной точке.

Условие равновесия плоской системы сходящихся сил в геометрической форме: плоская система сходящихся сил находится в равновесии, если силовой многоугольник, построенный из этих сил, является замкнутым.

Условие равновесия плоской системы сходящихся сил в аналитической форме: для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы алгебраические суммы проекций всех сил системы на каждую из двух взаимно перпендикулярных осей координат были равны нулю.

Уравнения равновесия системы сходящихся сил:

.

Решение задач на равновесие несвободного твердого тела, к которому приложена система сходящихся сил, можно выполнить двумя способами: 1 – геометрическим; 2 – аналитическим.

Решение задач геометрическим способом рекомендуется выполнять в следующем порядке:

1.  Выделить тело (или точку), равновесие которого следует рассмотреть.

2.  Изобразить все активные (заданные) силы.

3.  Применить принцип освобождения от связей, заменив их действия на точку реакциями связей.

4.  Построить замкнутый силовой многоугольник в следующем порядке:

○  выбрать масштаб , где F – модуль известной по величине силы в заданной системе (или один из модулей сил, если сил несколько); ав – длина отрезка, изображающего вектор силы в силовом многоугольнике;

○  построить вектор известной силы из произвольной точки а;

○  через конец и начало вектора известной силы провести направления неизвестных реакций до их пересечения;

○  указать направления реакций, учитывая, что силовой многоугольник должен быть замкнут;

○  для определения модулей реакций измерить длину отрезков, изображающих реакции и умножить их на масштаб.

Решение задач аналитическим методом рекомендуется выполнять в следующем порядке:

○  выделить тело (точку), равновесие которого следует рассмотреть;

○  изобразить задаваемые силы;

○  применить принцип освобождения от связей, т. е. мысленно отбросить связи и заменить их действие соответствующими реакциями;

○  выбрать в плоскости действия сил систему декартовых координат хоу;

○  определить углы между направлением всех сил и осями координат;

○  составить уравнения равновесия:

∑ FKX = 0; ∑ FKУ = 0;

○  решить систему составленных уравнений и определить искомые величины.

Задание 1. Определить реакции связей для заданной стержневой системы. Данные взять из табл. 1.

Варианты к заданию 1

Таблица 1

Пример № 1

Задача на определение реакций невесомых стержней

Груз Р = 80 кН поднимается лебедкой при помощи каната, перекинутого через неподвижный блок А. Определить усилия, возникающие в стержнях АВ и АС, поддерживающих блок А. Трением в блоке и его размерами пренебречь.

Усилия в стержнях равны по модулю реакциям стержней и противо-

положно им направлены, поэтому для определения усилий в стержнях вычислим реакции стержней и .

Решаем задачу аналитическим способом.

Рассмотрим равновесие блока А (рис. 9), представив его в виде материальной точки свободного тела, для чего освободим блок А от связей, заменив их реакциями стержней и . Тогда на блок А действуют четыре силы: натяжение левой ветви нити, равное , натяжение правой ветви нити , равное по величине также Р(Т = Р) и реакции стержней и , направленные вдоль стержней от узла (истинное направление реакций стержней уточняется по ходу решения задачи).

Выберем систему координат.

Это можно сделать двумя способами.

I способ.

За начало координат возьмем точку А, ось Х направим горизонтально вдоль линии действия силы , ось У проводим перпендикулярно оси Х.

Для плоской системы сходящихся сил составляем два уравнения равновесия:

∑FKX = 0; T - S1 × cos60° - S2 × cos30° = 0 (1)

∑FKУ = 0; S1 × cos30° - S2 × cos60°- P = 0 (2)

Решаем полученную систему методом подстановки, т. к. каждое уравнение имеет по две неизвестные величины.

Из уравнения (I) выразим величину реакции S1:

. (3)

Подставим значение S1 в уравнение (2) и решим его:

Подставим числовые значения в полученное выражение:

Из выражения (3) определим:

II способ.

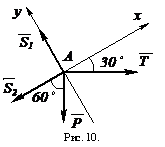Проведем одну из осей, например, ось Х по неизвестной реакции (рис. 10). Тогда, учитывая, что стержни АВ и АС взаимно перпендикулярны, ось у пройдет по направлению реакции . Составим уравнения равновесия в этой системе осей:

∑FKX = 0; - S2 + Т × cos30° - Р× 60° = 0;

∑FKУ = 0; S1 – Р × 30° - Т × 60° = 0.

Из уравнений находим:

S2 = T × 30° - P × 60° = 80 × 0,866 – 80 × 0,5 = 29,3 кН;

S1 = Р × 30° + Т × 60° = 80 × 0,866 + 80 × 0,5 = 109,3 кН.

Сравнивая решения двумя способами, заключаем, что второе решение рациональней, т. к. при данной системе координат в каждом уравнении равновесия имеется только одна неизвестная реакция. Решение таких уравнений гораздо проще, чем в первом случае.

Полученные значения реакций связей положительны, следовательно, первоначально, выбранные направления соответствуют действительности.

Оба стержня растягиваются.

Для проверки правильности решения задачи достаточно вычислить алгебраическую сумму проекций всех сил на любую ось, которая не использовалась в решении, но проходит через точку А. Если реакции определены верно, то в результате вычислений получится 0.

Например: при решении задачи 1 способом, вычислим алгебраическую сумму проекций на ось, совпадающую с направлением силы S2 (рис. 10):

∑FKX =- S2 – Р × 60° + Т × 30° =

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10