6.3. Дифференциальные зависимости при изгибе

Ранее были получены дифференциальные зависимости между интенсивностью распределенной нагрузки , поперечной силой и изгибающим моментом :

; ; . (6.8)

Кроме того, были получены дифференциальные зависимости между прогибом и углом поворота, прогибом и изгибающим моментом, углом поворота сечения и изгибающим моментом:

; ; . (6.9)

Эти зависимости, после некоторого преобразования, можно расположить последовательно:

(6.10)

Из этих уравнений видно, что, зная нагрузку и устройство опор балки, можно последовательным интегрированием получить величины , , , . С другой стороны, зная уравнение упругой линии, можно путем последовательного дифференцирования по из функции получить , , и . Для графического изображения этих зависимостей условимся положительные значения всех перечисленных величин откладывать вверх, а отрицательные – вниз; положительное направление оси в правой системе координат примем вправо, поворот сечения по часовой стрелке – отрицательным, а против – положительным. В левой системе координат – наоборот.

Приведем несколько примеров построения эпюр распределения поперечных сил, изгибающих моментов, углов поворота сечений и прогибов.

Пример 6.6. Построить качественные эпюры распределение поперечных сил, изгибающих моментов, углов поворота сечений и прогибов, для балки, изображенной на рис. 6.8.

Рис.6.8

Пример 6.7. Построить качественные эпюры распределения поперечных сил, изгибающих моментов, углов поворота сечений и прогибов, для балки, изображенной на рис. 6.9.

Рис.6.9

При построении эпюр углов поворота и прогибов следует придерживаться некоторых правил. Сформулируем их:

1. Так как представляет собой диаграмму производной от эпюры углов поворота , то ординаты эпюры пропорциональны тангенсу угла наклона касательной к эпюре . В сечениях, где , касательная к кривой должна быть параллельна оси абсцисс (Рис.6.8 - сечение А и 6.9 - сечения А и В). Скачку на эпюре моментов соответствует угловая точка на эпюре (Рис.6.8 – сечение А и 6.10 – сечение С).

2. Вторая производная прогиба

имеет знак момента. Если момент положителен (сжаты верхние волокна), то вогнутость на эпюре будет обращена в сторону положительных прогибов (вверх). При отрицательном моменте вогнутость пораболы обращена вниз. Так как ординаты эпюр изгибающих моментов мы условились откладывать со стороны сжатых волокон, то вогнутость эпюры прогибов всегда обращена в ту сторону, с которой расположены ординаты эпюры изгибающих моментов.

Рис.6.10

3. Вторая производная угла поворота

имеет знак поперечной силы. Если положительна, то выпуклость на эпюре будет обращена вниз (Рис.6.8, 6.9). При выпуклость направлена в сторону оси , т. е. вверх (Рис.6.9). В сечении, где меняет знак, на эпюре наблюдается точка перегиба. (Рис.6.9).

4. Если изгибающий момент равен нулю на протяжении какого-либо участка балки, то на этом участке угол поворота не меняется, а прогиб меняется по линейной зависимости.

5. На тех участках балки, где эпюра изменяется по линейному закону, эпюра меняется по закону квадратной параболы, а эпюра - по закону параболы третьего порядка. Там, где эпюра изменяется по закону квадратной параболы, эпюра меняется по закону параболы третьего порядка, а эпюра - по закону параболы четвертого порядка.

6. На участках, где действует постоянный момент, эпюра меняется по линейному закону, а эпюра прогибов меняется по закону квадратной параболы.

7. Так как представляет собой график изменения по длине балки тангенсов наклона касательных к упругой линии, то можно утверждать следующее:

а) на участках, где в направлении оси прогиб возрастает, угол наклона будет положителен. Наоборот, при уменьшении углы наклона будут отрицательны (Рис.6.10, участок АС);

б) в сечениях, где , касательная к эпюре горизонтальна, т. е. в этом сечении на эпюре наблюдается аналитический максимум или минимум (Рис.6.9).

Рассмотрим еще несколько примеров построения эпюр углов поворота и прогибов.

Пример 6.8. Какая из эпюр углов поворота соответствует приведенной на рис.6.11 эпюре изменения прогибов, представляющей собой параболу четвертого порядка?

Решение:

Вариант а) отпадает, так как эпюра углов поворота может меняться по линейному закону лишь в том случае, если эпюра прогибов представляет собой квадратную параболу.

Вариант б) не подходит по той причине, что максимального значения прогиб достигает в сечении, в котором угол поворота равен нулю. Такого соответствия в этом варианте нет.

Вариант в) не подходит, так как на левой части эпюры прогиб убывает слева направо при положительном тангенсе угла наклона касательной к кривой прогибов. В этом варианте нет соответствия между знаком приращения прогиба и знаком эпюры углов поворота.

Вариант г) подходит по ряду признаков: во-первых, совпадают знаки приращения прогиба и знаки угла поворота на всей длине участка. Во-вторых, экстремального значения прогиб достигает в сечении, в котором угол поворота равен нулю. В-третьих, в сечениях на левом и правом концах участка, там, где прогиб равен нулю, касательная к кривой углов поворота параллельна базисной линии, что соответствует равенству нулю тангенса угла поворота в этих сечениях.

Таким образом, из четырех вариантов эпюра изменения углов поворота соответствует эпюре изменения прогибов в последнем варианте.

Пример 6.9. Какая из эпюр прогибов соответствует представленной на рис.6.12 эпюре изгибающих моментов, если положительное направление оси направлено вверх?

Рис.6.12

Решение:

Вариант а) не подходит, так как положительному изгибающему моменту в выбранной ситеме координат должна соответсвовать положительная кривизна упругой линии балки. Такого соответствия здесь нет.

Вариант б) не подходит по той причине, что изогнутая ось балки имеет кривизну одного и того же знака на всей длине участка, в то время как изгибающий момент меняет знак по длине участка.

Вариант в) не подходит по той же причине.

Вариант г) подходит, так как имеет место соответствие знаков изгибающего момента и знаков кривизны изогнутой оси на соответствующих участках.

6.4. Определение перемещений в балках методом начальных параметров

Этот метод определения перемещений в балках относится также к методам аналитическим. При использовании метода непосредственного интегрирования упругой линии балки нам приходилось определять постоянные интегрирования и . При одном участке таких постоянных было две. С увеличением числа участков количество постоянных интегрирования растет вдвое. Так, если балка по условиям нагружения имеет участков, то интегрирование дифференциальных уравнений для всех участков балки дает произвольных постоянных. Из граничных условий опирания балки можно найти всего 2 постоянные интегрирования. Остальные постоянные приходится определять из условия непрерывного и плавного сопряжения для всех участков упругой линии. В результате мы получаем систему уравнений степени , решение которой уже при вызывает серьезные сложности, учитывая процедуру составления дополнительных уравнений совместности деформаций. Эта громоздкая и кропотливая работа делает метод непосредственного интегрирования практически неприменимым для балок с большим числом участков.

Между тем, существует возможность решения подобных задач путем сведения всех постоянные интегрирования к двум независимо от числа участков. Этот метод получил название метода начальных параметров. Разработан этот метод советскими учеными , , Безухим Н. И., и др.

В соответствии с этим методом сведение всех постоянных интегрирования к двум – прогибу и углу поворота в начале координат – при любом числе участков стало возможным при выполнении следующих условий:

1. Начало кроординат необходимо выбирать в крайней левой (или правой) точке рассматриваемой балки и делать его общим для всех участков балки.

2. Выражение для изгибающего момента составлять, вычисляя моменты сил, расположенные по одну сторону от рассматриваемого сечения со стороны начала координат.

3. При включении в уравнение внешнего сосредоточенного момента его следует умножать на множитель , равный единице, где - абсцисса точки, в которой приложен момент .

4. В случае обрыва распределенной нагрузки ее продлевают до рассматриваемого сечения, а для восстановления действительных грузовых усилий вводят “компенсирующую” нагрузку обратного направления.

5. Интегрирование уравнений на всех участках следует производить, не раскрывая скобок.

Рассмотрим балку (Рис.6.13), нагруженную группой сил. Начало координат поместим на левом конце балки в точке и составим уравнение изгибающих моментов для крайнего четвертого участка:

(6.11)

Рис.6.13

Исследуя рис.6.13 легко можно увидеть, что из уравнения (6.11) изгибающий момент на IV участке получается путем вычеркивания членов, появляющихся лишь на V участке:

. (6.12)

Остальные члены, входящие в уравнение (6.12) остаются такими же. Следует отметить, что коэффициенты ,,,….,, входящие в уравнение изгибающих моментов, могут иметь только положительные значения. Если окажется, что , то это означает, что соответствующая нагрузка расположена справа от рассматриваемого сечения, если начало координат лежит слева от сечения, или расположена слева от рассматриваемого сечения, если начало координат лежит справа от сечения. В дальнейшем для вывода окончательных выражений для перемещений будем считать, что начало координат расположено на левом конце балки (Рис.6.13).

Составим дифференциальное уравнение упругой линии для участка V:

. (6.13)

Интегрируя первый раз обе части равенства (6.13), не раскрывая скобок, получим:

. (6.14)

Инрегрируем второй раз:

. (6.15)

Дифференциальное уравнение на IV участке примет вид:

. (6.16)

Проинтегрировав это уравнение дважды получим:

. (6.17)

. (6.18)

Вычислим теперь угол поворота сечения , лежащего на стыке участков IV и V. Из условия плавного сопряжения участков получим:

. (6.19)

Откуда: .

Принимая и подставляя в уравнения (6.18) и (6.15), из условия непрерывного сопряжения участков находим:

.

Выполнив аналогичные операции для остальных участков, получим:

;

.

Определим геометрический смысл постоянных интегрирования. Для этого найдем угол поворота и прогиб в начале координат при . Это сечение принадлежит первому участку. Составим уравнение углов поворота и прогибов для первого участка, вычеркнув в уравнениях (6.14) и (6.15) слагаемые, учитывающие нагрузки, приложенные на II – V участках:

; (6.20)

. (6.21)

Подставляя в эти уравнение , получим:

; (6.22)

. (6.23)

Таким образом, произвольные постоянные и 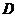равны соответственно углу поворота и прогибу в начале координат и , которые принято называть геометрическими начальными параметрами. Подставляя в уравнение (6.15) вместо постоянных интегрирования и 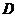равные им значения начальных параметров, получаем:

. (6.24)

Если на балку действует несколько моментов и сил, а также несколько участков распределенной нагрузки, уравнение для прогибов можно составить в следующем виде:

(6.25)

Уравнение (6.25) обычно называют универсальным уравнением упругой линии.

Продифференцировав уравнение (6.25), получим уравнение углов поворота сечения:

. (6.26)

Здесь и в формуле (6.25) приняты следующие обозначения: - тип внешнего силового фактора (); - показатель степени, получаемый при интегрировании дифференциального уравнения упругой линии; - координата сечения, в котором приложена сросредоточенная сила или момент, или координата сечения, к котором начинается действие распределенной нагрузки. Соответствие величины показателя степени типу внешнего фактора приведено в таблице 6.1.

Таблица 6.1

Знаки слагаемых в уравнения (6.25) и (6.26) определяются знаком изгибающего момента, который вызывается соответствующим силовым фактором.

Характерной особенностью метода начальных параметров является то, что для определения перемещения нет необходимости составлять и интегрировать дифференциальное изогнутой оси балки. Достаточно составить универсальное уравнение упругой линии (6.25), из условий на опорах найти начальные параметры и снова воспользоваться универсальным уравнением, чтобы найти прогиб в рассматриваемом сечении.

Рассмотрим пример определения перемещений по методу начальных параметров.

Пример 6.10. Определить прогиб посредине пролета балки, приведенной на рис.6.14, и угол поворота сечения С на левом конце балки. Материал балки - сталь с модулем упругости МПа. Балка представляет собой двутавр № 20 с моментом инерции см4.

Решение:

1. Определим опорные реакции. Для этого составим два уравнения равновесия:

. Откуда кН;

. Откуда кН.

2. Помещаем начало координат на правом конце балки в точку В, ось прогибов направляем вверх, ось - влево. Чем в данном случае определен выбор начала координат? Если выбрать начало координат на левом конце балки в сечении С, то предварительно придется искать оба начальных параметра, так как ни угол поворота сечения С, ни прогиб в этом сечении заранее неизвестны. Для их определения потребуется составлять систему из двух уравнений и решать ее относительно двух неизвестных начальных параметров. Если же выбрать начало координат на правом конце балки в сечении В, то находить придется лишь один начальный параметр – угол поворота сечения В . Второй начальный параметр – прогиб в сечении В – искать не нужно, так как он равен нулю из граничного условия на опоре В.

3. Разбиваем балку на участки (Рис.6.14) и записываем универсальное уравнение упругой линии (6.25) для последнего участка:

(а)

4. Из уравнения (а) определяем начальный параметр из условия, что прогиб в сечении А при м равен нулю:

.

Откуда

.

5. Определяем прогиб посредине пролета балки при м. Так как сечение посредине балки принадлежит первому участку, вычеркиваем из универсального уравнения все члены, принадлежащие второму и третьему участкам. Получим:

.

Подставляем численные значения модуля упругости и момента инерции в полученное выражение. Получаем:

м =- 44,3мм.

Знак “-” означает, что направление прогиба не совпадает с направлением оси прогибов .

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3