ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ВОЛГОГРАДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
КАМЫШИНСКИЙ ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ (ФИЛИАЛ)
ВОЛГОГРАДСКОГО ГОСУДАРСТВЕННОГО ТЕХНИЧЕСКОГО УНИВЕРСИТЕТА
Кафедра «ОБЩЕТЕХНИЧЕСКИЕ ДИСЦИПЛИНЫ»
РАСЧЕТ НА ПРОЧНОСТЬ
И ЖЕСТКОСТЬ БАЛКИ
ПРИ ПРЯМОМ ИЗГИБЕ
Методические указания к практическим занятиям
по дисциплине «Сопротивление материалов».
РПК «Политехник»
Волгоград
2006
УДК 539. 3/6 (07)
P 24
Расчет на прочность и жесткость балки при прямом изгибе: Методические указания к практическим занятиям по дисциплине «Сопротивление материалов» / Сост. ; Волгоград. гос. техн. ун-т. – Волгоград, 2006. – 43 с.
Содержат краткие теоретические положения о деформации плоский прямой изгиб; методы расчетов на прочность и жесткость статически определимых балок; варианты и пример выполнения индивидуальных заданий.
Предназначены для студентов обучающихся по направлениям 551200 (код ОКСО 260700) «Технология и проектирование текстильных изделий», 552900 (код ОКСО 150900) «Технология, оборудование и автоматизация машиностроительных производств». Также рекомендуются для студентов направления 551700 (код ОКСО) «Электроэнергетика».
Ил. 23. Табл. 2. Библиогр.: 3 назв.
Рецензент: к. т. н.
Печатается по решению редакционно-издательского совета
Волгоградского государственного технического университета
Корзун
РАСЧЕТ НА ПРОЧНОСТЬ И ЖЕСТКОСТЬ БАЛКИ ПРИ ПРЯМОМ ИЗГИБЕ
Методические указания к практическим занятиям
по дисциплине «Сопротивление материалов».
Под редакцией автора
Темплан 2006 г., поз. № 9.
Подписано в печать г. Формат 60×84 1/16.
Бумага листовая. Печать ризографическая.
Усл. печ. л. 2,69. Усл. авт. л. 2,56.
Тираж 100 экз. Заказ №
Волгоградский государственный технический университет
400131 Волгоград, просп. им. , 28.
РПК «Политехник»
Волгоградского государственного технического университета
400131 Волгоград, ул. Советская, 35.
© Волгоградский
 государственный
государственный
технический университет, 2006
Тема: Расчет на прочность и жесткость балки при прямом изгибе.
Цель занятия: освоить построение эпюр поперечных сил и изгибающих моментов, определение нормальных и касательных напряжений, подбор сечений балки и определение перемещений методом начальных параметров.
Время выполнения: 6 часов.
1. ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
1.1. Внешние силы
Брус, работающий на изгиб называется балкой.
Плоскость, содержащая продольную ось балки и одну из главных центральных осей инерции ее поперечного сечения, называется главной плоскостью балки (рис. 1.).
 |
Плоскость действия сил называется силовой плоскостью.
Линия пересечения силовой плоскости с плоскостью поперечного сечения называется силовой линией.
Деформация плоский прямой изгиб имеет место в случае действия на брус уравновешенной системы перпендикулярных его оси сил, плоскость действия которых совпадает с главной плоскостью балки.
1.2. Механизм деформации
В результате такого действия сил на балку происходит следующее (рис. 2):
· Продольная ось балки искривляется, превращаясь в плоскую кривую, расположенную в силовой плоскости. Это отличительная особенность деформации прямой изгиб от других видов простого сопротивления: например растяжения (сжатие), кручение, при которых продольная ось оставалась прямолинейной.
· Все волокна балки искривляются, не надавливая друг на друга; при этом с выпуклой стороны они претерпевают растяжение; а с вогнутой – сжатие. Это означает, что каждый элемент волокна испытывает центральное растяжение или сжатие.
· Поперечные сечения балки поворачиваются вокруг главной центральной оси, перпендикулярной силовой линии, оставаясь при этом плоскими и перпендикулярными деформированной оси балки.
Слой волокон, который является границей между зоной растяжения и зоной сжатия и который не испытывает ни растяжения, ни сжатия, а только искривляется, называется нейтральным слоем.

Линия пересечения нейтрального слоя с плоскостью поперченного сечения называется нейтральной осью.
1.3. Внутренние силовые факторы
В зависимости от схемы нагружения балки в ее поперечных сечениях могут возникать:
· один внутренний силовой фактор – изгибающий момент Мх;
· два внутренних силовых фактора – изгибающий момент Мх и поперечная сила Qy.
Случай изгиба, при котором в поперечном сечении действует только изгибающий момент, называется чистым изгибом.
Изгиб, при котором в поперечных сечениях действуют одновременно и поперечная сила, и изгибающий момент, называется поперечным изгибом.
С точки зрения внутренних сил упругости:
· поперечная сила есть равнодействующая внутренних касательных к сечению сил упругости ![]() (рис. 3 а);
(рис. 3 а);
· 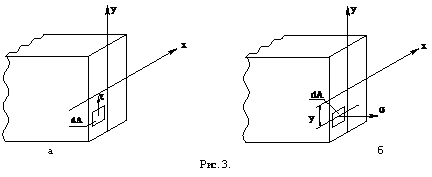
изгибающий момент есть момент результирующей пары внутренних, нормальных к сечению сил упругости ![]() (рис. 3 б).
(рис. 3 б).
Для расчета на прочность балок необходимо знать наибольшее значение Q и M и положение сечений, в которых они действуют (опасных сечений).
|
Эпюрой поперечных сил (изгибающих моментов) называется графическое изображение закона изменения величины поперечной силы (изгибающего момента) по длине балки.
Характерными сечениями (точками) балки являются:
· концевые сечения балки;
· сечения в которых приложены нагрузки (точки приложения сосредоточенных сил и моментов, начало и конец действия распределенной нагрузки).
Чтобы определить величину поперечной силы и изгибающего момента необходимо сделать следующее:
1. Определить опорные реакции балки.
2. Обозначить характерные точки.
3. Мысленно разрезать балку сечением, отбросить более сложную часть балки (ту к которой приложено больше сил), и составить выражение для определения Q (а затем М) пользуясь правилами.
Правила для определения поперечной силы.
1. Поперечная сила Qy численно равна алгебраической сумме проекций всех внешних сил, приложенных к оставшейся части балки, на ось Y.
 .
.
2. Если при подходе к сечению слева внешняя сила направлена снизу вверх, то ее следует взять со знаком «+», а если сверху вниз – то со знаком «-» (рис. 4 а).
При подходе к сечению справа используется обратное правило знаков (рис. 4 б).
Возможна и иная интерпретация правила знаков для поперечной силы.
Если внешняя сила стремиться повернуть оставшуюся часть балки относительно рассматриваемого сечения по часовой стрелке, то ее следует взять со знаком «+», а если против часовой, то со знаком «-» (см. рис. 4).

Правила для определения изгибающего момента.
1. Изгибающий момент численно равен алгебраической сумме моментов внешних сил, приложенных к оставшейся части балки, относительно центра тяжести рассматриваемого сечения.
 ,
,
где точка с – центр тяжести рассматриваемого сечения.
2.
 |
Правило знаков. Если внешняя сила изгибает балку относительно рассматриваемого сечения выпуклостью виз, то ее момент следует взять со знаком «+», а если выпуклостью вверх, то со знаком минус (рис. 5).
Примечание:
· сечение, в котором определяется изгибающий момент, жестко закрепляем;
· действие каждой силы рассматривается в отдельности.
Правило знаков для изгибающего момента может иметь и другое истолкование.
Если внешняя сила стремиться повернуть оставшуюся часть балки по часовой стрелке, относительно рассматриваемого сечения при подходе к сечению слева, то ее момент следует взять со знаком «+», а если против часовой стрелки, то со знаком «-».
При подходе к сечению справа используется обратное правило знаков.
По полученным значениям Q и M стоят эпюры, аналогично тому, как в свое время строились эпюры «Nz» и «Mz».
При построении эпюры «Q» положительные значения откладывают вверх, а отрицательные вниз от оси.
При построении эпюры «М» положительные значения откладывают вверх от оси, а отрицательные вниз, т. е. эпюра изгибающих моментов строится со стороны сжатых волокон балки.
По окончании построения эпюр «Q» и «М» необходимо проверить правильность их построения.
Правила контроля эпюр «Q» и «М» вытекают из дифференциальных зависимостей Журавского между q, Q и М и основаны на геометрическом смысле I производной.

Первая производная от данного значения функции по данному значению аргумента есть тангенс угла наклона касательной к графику функции в точке, абсцисса которой равна данному значению аргумента.
Так, например, на основании зависимости ![]() следует, что если
следует, что если
q = 0, то и угол наклона касательной к графику функции«Q» (эпюра «Q») равен 0, т. е. эпюра «Q» изображается прямой, параллельной оси эпюры (рис. 6 а).
Если q ≠ 0, и q = const это означает что касательная к графику функции Q (к эпюре «Q») имеет постоянный угол наклона, а это значит, что эпюра «Q» изображается прямой, наклонной к оси эпюры (рис. 6 б).
Аналогично использование зависимости:

Правила контроля эпюр основаны также и на свойстве первой производной: если первая производная положительна, то функция возрастает; если первая производная отрицательна – то убывает.
 |
Экстремум (максимум или минимум) функции имеется при тех значениях аргумента, при которых первая производная равна нулю, т. е. касательная к графику функции параллельна оси абсцисс (рис. 7).
Основываясь на выше рассмотренном, правила контроля эпюр можно свести к следующему.
Контроль эпюры «Q» (рис. 8 а) (производится слева направо).
Предположим, что материальная точка стремится двигаться по горизонтальной линии, на которой построена эпюра «Q», начиная от точки, соответствующей левому концу балки, и кончая точкой, соответствующей правому, но, попадая на линию действия силы, она смещается этой силой на величину силы по направлению ее действия.
Например: (рис. 8 а) точка смещается вниз на величину VA = 10 кН. Затем точка движется горизонтально до сечения С.
Дальше равномерно распределенная нагрузка q1 смещает постепенно точку вниз; к концу участка (точка D). Общая высота смещения составит 30 кН, то есть поперечная сила в сечении D QD = (10 + 30 = 40 кН), 30 = qI × lСД = 30 × 1 = 30. Затем сила F смещает точку вверх на величину 30 кН. Далее нагрузка q2 постепенно смещает точку вверх; общая высота смещения точки к концу участка (точка В) должна составить q2 × lDВ = 20 × 1 = 20 кН.
|
Точка вышла из оси и вернулась на ось, значит, эпюра «Q» построена правильно.
Контроль эпюры «М» (рис. 8 б).
· В сечениях балки, где действует сосредоточенный момент на эпюре, имеется скачек, равный по величине этому моменту (сечение А) m - 35 кН×м.
·
 |
На участках балки, свободных от распределенной нагрузки, эпюра «М» изображается прямой, наклонной оси эпюры (участок АС).
· На участках балки, где действует распределенная нагрузка, эпюра «М» изображается параболой, выпуклость которой обращена в сторону противоположную действию нагрузки q (участок СD – выпуклость параболы обращена вверх; на участке ВD выпуклость параболы обращена вниз).
· В сечениях, где приложена сосредоточенная сила, на эпюре «М» имеется излом, острие которого направлено в сторону противоположную действию силы (сечение D).
· Если поперечная сила положительна, то изгибающий момент возрастает, если отрицательна то убывает (участок АС и СD Q < 0 изгибающий момент убывает – эпюра М «идет» вниз, в «-», то же на участке DК; на участке КВ, где Q > 0, изгибающий момент возрастает эпюра «М» идет вверх в «+»).
1.4. Общий порядок определения величины
поперечных сил и изгибающих моментов
1. Составляется расчетная схема балки с изображением действующих на нее внешних сил активных и реактивных и определяется величина неизвестных опорных реакций (для консолей определять реакции не обязательно).
2. Балка разбивается на участки, границами которых являются:
· точки приложения сосредоточенных сил;
· точки приложения сосредоточенных пар сил;
· начало и конец распределения нагрузки, проводится ось эпюры, параллельно оси балки.
Границы участков переносятся на ось эпюры.
3. На каждом участке составляются уравнения для изгибающего момента «М» и поперечной силы «Q» согласно зависимости 1 и 2 и правилам знаков.
4. По полученным уравнениям определяются значения «М» и «Q» для характерных точек (границ участков). По полученным значениям «Q» и «М» строят график зависимости Q и М от Z.
При этом:
· положительные значения поперечной силы и изгибающего момента откладываются вверх от оси,– (эпюра М строится на сжатых волокнах).
5. Если на каком-либо участке эпюра «Q» изменяясь по линейному закону пересекает ось эпюры в точке К, следовательно в этой точке
Q = 0, и здесь необходимо определить экстремальное значение М (рис. 8 а).
6. Расстояние от начала участка до сечения, в котором Q = 0, (Zк) определяют как частное от деления значения Q в крайнем сечении этого участка, на интенсивность нагрузки q:
 .
.
1.4.1. Построение эпюр «М» и «Q» для балок
на 3 участка (аналитический метод)

Пример. Для заданной расчетной схемы балки построить эпюры поперечных сил и изгибающих моментов (рис. 9 а).
Определяем опорные реакции:
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
Проверка:
 .
.
· Разбиваем балку на участки. Границы участков – точки приложения сосредоточенных сил и пар сил, начало и конец распределенной нагрузки.
· Рассматриваемая балка имеет 3 участка: I – AC; II – CB; III – BD.
· Построение эпюры «Q» (рис. 9).
 Участок АС – рассмотрим сечение 1-1 на расстоянии Z1, от левой опоры. Абсцисса на участке АС меняется по величине в пределах от 0 до 2 м, 0 £ Z1 ³ 2 (рис. 10).
Участок АС – рассмотрим сечение 1-1 на расстоянии Z1, от левой опоры. Абсцисса на участке АС меняется по величине в пределах от 0 до 2 м, 0 £ Z1 ³ 2 (рис. 10).
Составим уравнение проекций всех сил, расположенных слева от сечения на ось у:
 , Q = VA,
, Q = VA,
т. е. величина Q1 не зависит от Z1. Q1 = 3 (кН).
Следовательно, эпюра «Q» на участке АС имеет вид прямой, параллельной оси Z (рис. 9).
Участок СВ – 0 £ Z2 £ 4 рассмотрим левую часть балки (рис. 11):

![]() ,
,
при Z2 = 0 QС = VA – F – 0 = 1 (кН),
при Z2 = 4 QВ = VA – F – q × 4 = -7 (кН)
Очевидно, что эпюра «Q» представляет прямую, наклонную к оси эпюры, которая пересекает эту ось в некоторой точке К. Определяем расстояние от этой точки до точки С:
QК = 0; Z2 = ZК,
VA – F – q × ZК = 0, ![]() .
.
 Участок ДВ – (0 £ Z3 £ 2 м) рассмотрим правую часть балки (рис. 12):
Участок ДВ – (0 £ Z3 £ 2 м) рассмотрим правую часть балки (рис. 12):
 ,
,
эпюра совпадает с осью Z (рис. 9).
Построение эпюры «М».
Участок АС – рис. 10. (0 £ Z1 £ 2 м),
М1 = å m1(Fлев) = VA × Z1 = 3Z1 – прямая пропорциональная зависимость.
При Z1 = 0 МА = 0.
При Z1 = 2 МС = 3 × 2 = 6 кН×м.
Участок СВ – рис. 11. (0 £ Z2 £ 4 м),
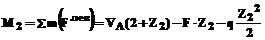 – квадратная парабола.
– квадратная парабола.
При Z2 = 0 МС = 3 × 2 = 6 кН м.
При Z2 = 0,5 м ![]() кН×м.
кН×м.
При Z2 = 4 м ![]() кН м.
кН м.
По трем точкам строим эпюру (рис. 9).
Участок DB – рис.12. (0 £ Z3 £ 2 м); M3 = - m = const, M3 = -6 кН×м – прямая параллельная оси Z.
· Проверяем правильность построения эпюр по правилам контроля.
Индивидуальные задания по построению эпюр «Q» и «М» смотреть в приложении.
1.5. Напряжения в поперечном сечении
В случае прямого поперечного изгиба в поперечных сечениях балки возникают нормальные (σ) и касательные (τ) напряжения.
Нормальные напряжения распределяются по высоте по линейному закону и в любой точке сечения определяются по формуле:

где Мх – изгибающий момент, действующий в данном сечении (берется из эпюры «М»);
Jх – осевой момент инерции сечения относительно нейтральной оси;
y – расстояние от точки, в которой определяется напряжение, до нейтральной оси.
Знак у напряжения устанавливается по физическому смыслу.
Если точка находится в растянутой зоне, то напряжение σ в этой точке имеет знак «+», а если в сжатой зоне, то «-».
При положительном изгибающем моменте балка искривляется выпуклостью вниз(рис. 9 а, б)., то есть точки а и в находятся в растянутой зоне и напряжение в этих точках положительны: σа > 0; σb > 0, а напряжение в точках, расположенных выше нейтральной оси отрицательны σс < 0.

При отрицательном изгибающем моменте (рис. 13 в) точки а и в сечения находятся в сжатой зоне и нормальные напряжения в этих точка отрицательны.
По ширине сечения величина нормальных напряжений не меняется, т. е. постоянна для всех точек, находящихся на одном и том же уровне σa = σв (рис. 13 а).
Наибольшие по величине нормальные напряжения возникают в крайних верхних и нижних точках сечения (опасные точки) и определяются по формуле:
 ,
,
где Wx – момент сопротивления сечения относительно нейтральной оси.
![]()
![]()
![]()
![]() Для сечения простой формы Wх определяется
Для сечения простой формы Wх определяется
по формулам, для проката – по таблицам сортамента.
Таблица 1
форма сечения |
|
|
|
|
|
|
Wx |
|
| 0,1×D3 | 0,1×D3×(1-C4)
| По табл. сортамента | По табл. сортамента 2×Wx и 2×Ix |
Ix |
|
| 0,5×D4 | 0,5×D4×(1-C4) | ||
τmax |
|
|
|
|
|
|
1.6. Касательные напряжения
Касательные напряжения также постоянны по величине в точках, находящихся на одном и том же уровне, а по высоте сечения изменяются по криволинейному закону. Например, для прямоугольного сечения и производных от него по закону квадратной параболы.
В любой точке поперечного сечения касательные напряжения определяются по формуле Журавского:
 ,
,
где Q – поперечная сила, действующая в данном поперченном сечении (берется из эпюры «Q»);
![]() – статический момент отсеченной части сечения (расположенной выше или ниже уровня данной точки) относительно нейтральной оси;
– статический момент отсеченной части сечения (расположенной выше или ниже уровня данной точки) относительно нейтральной оси;
Jх – момент инерции сечения относительно нейтральной оси;
b – ширина сечения на уровне рассматриваемой точки.
В отличие от нормальных напряжений, касательные напряжения максимальны в точках, принадлежащих нейтральной оси; в крайних же верхних и нижних точках сечения они равны нулю; касательные напряжения имеют один и тот же знак во всех точках сечения; он соответствует знаку поперечной силы. Если Q > 0, то и τ > 0 (рис. 13 г) при Q < 0 и τ < 0.
1.7. Напряженное состояние и главные напряжения
При чистом изгибе во всех точках балки имеет место линейное напряженное состояние, и наиболее опасными точками являются крайние верхние и нижние точки балки.
В случае поперечного изгиба напряженное состояние в различных точках по высоте балки неоднородно.
В крайних верхних и нижних точках балки напряженное состояние, как и в случае чистого изгиба линейное (рис. 14 а). Главные площадки здесь совпадают с поперечными сечениями и главные напряжения равны нормальным напряжениям, действующим в поперечных сечениях, т. е:
 .
.
В точках, расположенных в нейтральном слое, имеет место особый случай плоского напряженного состояния – чистый сдвиг, при котором по четырем граням, выделенного двумя поперечными и двумя горизонтальными сечениями элемента, действуют касательные напряжения (рис.14 б).

Главные напряжения равны в этом случае касательным напряжениям, действующим в площадках чистого сдвига (в поперечных сечениях) ![]() , а τmax зависят от формы сечения (см. табл. 1).
, а τmax зависят от формы сечения (см. табл. 1).
Главные площадки расположены под углом 45° к площадкам чистого сдвига.
В произвольных точках, расположенных выше или ниже нейтрального слоя имеет место плоское напряженное состояние (рис. 14 в).
Главные напряжения определяются по формулам:

где σa – нормальное напряжение, действующее в поперечном сечении;
τa – касательное напряжение в поперечном сечении.
Положение главных площадок определяется углом a0, между направлением главной площадки и площадки a (поперечным сечением):
 .
.
1.8. Расчет на прочность
В зависимости от постановки задачи различают три вида расчета на прочность.
1. Проверочный расчет, осуществляется:
· в сечении балки, где действует максимальный изгибающий момент в крайних верхних (нижних) точках сечения:
 ,
,
где [s] – допускаемое нормальное напряжение для материала балки;
· в сечении балки, где действует наибольшая по величине поперечная сила, в точках принадлежащих нейтральной оси по условию:
tmax £ [t],
где [s] – допускаемое нормальное напряжение для материала балки;
τmax определяется в соответствии с табл. 1;
· в сечениях балки, где действует одновременно значительные по величине поперечная сила и изгибающий момент в точках сечения, где действует значительное по величине нормальное и касательное напряжение по условию:
 ,
,
или:
 .
.
2. Проектный расчет осуществляется в следующем порядке:
· определяют требуемый момент сопротивления:

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 |







