Использование уравнения Шредингера в вязкой среде

Использование уравнения Шредингера в вязкой среде

Пользуясь аналогией между уравнением Шредингера и Навье Стокса, мнимая величина , где - постоянная Планка, масса частицы, имеющая размерность кинематической вязкости, рассматривается как мнимая кинематическая вязкость вакуума и к ней добавляется кинематическая вязкость среды, в которой находится тело. При этом уравнение Шредингера описывает вероятности при наличии усредненной кинематической вязкости системы. Полученное уравнение, может быть использовано в нанотехнологиях, для описания процессов в твердом теле, жидкости или газе.

Уравнение Шредингера решается для движения электронов вокруг ядра в вакууме см. [1]. Предлагается решать его для движения центра тяжести ядра атома в среде с учетом кинематической вязкости среды. При этом решение уравнения Шредингера соответствует статистическим значениям решения, что позволяет вводить такие статистические характеристики как вязкость. Тогда, так как величина в уравнении Шредингера играет роль кинематической вязкости, добавка к ней величины , где кинематическая вязкость жидкости, плотность жидкости, плотность тела, определяет уравнение

,

Подставляя временную зависимость 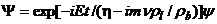(1)

в уравнение Шредингера, получим уравнение

,

где масса ядра, состоящего из нуклонов, и потенциал отличен от нуля на интервале. Построение одномерной координаты описано в книге [2]. При этом пространственные компоненты выражены в виде одной функции от трех переменных. Эти функции для разных состояний вещества - твердом, жидком и газообразном состоянии разные. Но они описываются одним уравнением, зависящим от одной функции одинаковым образом. Т. е. изменение симметрии при переходе из одного состояния в другое описывается инвариантно, за счет изменения связи функции 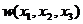с трехмерным пространством. При этом существует размер молекулы тела, при котором энергия молекулы определится одинаковой для всех одномерных координат. Обозначим этот характерный масштаб через . Тогда уравнение Шредингера имеет вид

, (2)

решение его приобретает вид

,

где параметр находится на отрезке 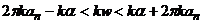с потенциальной энергией , где характеризует размер атома или молекулы, величина характеризует кристаллическую решетку, среднее расстояние между молекулами в жидкости или газе, если молекула находится в состоянии. При остальных значениях , находящихся вне атома или молекулы, имеем уравнение с нулевой потенциальной энергией

,

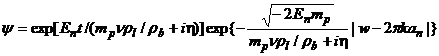причем отрицательно и определится из уравнений для равенства волновой функции и ее производной в точке .

,(3)

откуда получим уравнение инвариантное движению вдоль цепочки, которая определяет сдвиг на одну ячейку в трехмерном пространстве. Вычисляя эти выражения, получим

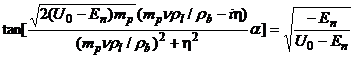, (4)

т. е. энергия состояния от размера цепочки не зависит, а наоборот энергия состояния определяет размер кристаллической цепочки по формуле 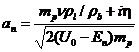и для разных энергий состояния системы эта величина разная. Так как для одной энергии состояния возможно большое, ограниченное количеством частиц, число реализаций состояний из-за принципа Паули, этих значений имеется несколько.

При получаем

.

Откуда имеем .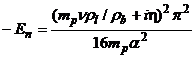

Полагаем , получим уравнение

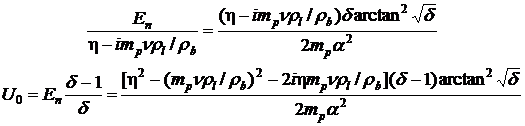(5)

Величина соответствует энергии осцилляторов минус энергия давления, равная давлению, умноженному на сумму объемов атомов. Тогда получим соотношение, определяющее энергию одного моля вещества 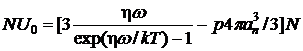. Величина это внешнее давление, включающее напряжение нагрузки, приложенной к телу, величина это постоянный размер решетки, или расстояние между атомами и молекулами, равный 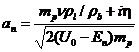, это число Авогадро. При этом из второго уравнения (5), приравнивая его энергии осцилляторов, определим размер атома или молекулы. Энергию осцилляторов можно определить по теплоемкости и температуре данного вещества.

При этом правые части уравнения (5) должны быть действительны, для образования стационарного состояния. Откуда определится дискретный набор комплексных значений , и значит дискретный набор стационарных состояний молекул вещества. Зная дискретный набор состояний тела, можно определять его фазовое состояние, и количества тепла, выделившегося при реакции перехода из одного состояния в другое. Для этого нужно вычислить энергию состояния вступающих в реакцию веществ и образовавшихся веществ. Использование данных идей позволило определить переход в пластическое состояние и вычислить энергию фазового перехода из жидкого состояния в газообразное состояние.

Литература

1.  , Квантовая механика Нерелятивистская теория М., «Наука», 1989г, 768с.

2.  Е. Якубовский Квазилинейные уравнения в частных производных LAP Lambert Academic Publishing, 2012г., 93с.