Лекция 18.

УРАВНЕНИЕ ШРЕДИНГЕРА
И ЕГО ЧАСТНЫЕ СЛУЧАИ:
СВОБОДНАЯ ЧАСТИЦА, бесконечно глубокая ПОТЕНЦИАЛЬНАЯ ЯМА

Уравнение Шредингера для волновой функции (1926) является нерелятивистским (то есть справедливо при скоростях частиц V << c) и ниоткуда не выводится, как и другие фундаментальные законы физики вроде законов динамики или закона Кулона. Встречающиеся в некоторых учебниках "выводы" несостоятельны. Общий вид уравнения:

, (18.1)

где i = - мнимая единица, U - функция координат и времени, характеризующая воздействие на частицу поля внешних сил - эта функция, если она не зависит от времени, равна просто потенциальной энергии; - так называемый оператор Лапласа (см. ЛЕКЦИЮ 9).

В декартовых координатах: (18.2)

и - радиус-вектор частицы. Её де-Бройлевскую волну можно записать в комплексной форме (17.8):

и, таким образом, временнáя и пространственная части волновой функции во многих важных случаях разделяются. Подставим последнее выражение в общее уравнение (18.1).

Поскольку , то

.

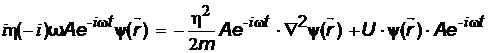Так как , то

. (18.3)

Это стационарное (т. е. не зависящее от времени) уравнение Шредингера. Начнем его анализ с простейшего случая.

Движение свободной частицы. Рассмотрим для простоты одномерный случай: имеется свободная частица (нет внешнего поля:
U = 0 ), которая может двигаться только вдоль оси Х. Нетрудно убедиться непосредственной подстановкой в общее уравнение (18.1), что решением этого уравнения является волна (или суперпозиция двух волн, распространяющихся навстречу друг другу). В соответствии с формулой Эйлера (17.7) комплексно сопряженная функция 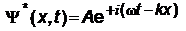и плотность вероятности нахождения частицы в любом участке оси Х равна Y×Y * = |Y|2 = A2 = const . Таким образом, свободной частице все равно, где находиться.

Частица в бесконечно глубокой потенциальной яме. Классическим аналогом этой задачи является эпизод с собакой Жучкой из "Детства Темы" -Михайловского, которую бросили в глубокий пересохший колодец (рис. 18.1). Понятно, что бедной классической Жучке было абсолютно все равно, в какой части дна вонючего колодца находиться.

Квантовая задача о частице в яме соответствует реальной ситуации связанных состояний электронов и других частиц в атомах и ядрах. Рассмотрим бесконечно глубокую одномерную яму шириной L. Внутри ямы при 0 < x < L потенциальная энергия U = 0, а слева и справа от нее (включая границы ямы) U = ¥, там частица находиться не может (рис. 18.2). Задача стационарная и описывается уравнением (18.3), которое для области ямы принимает вид , где

Поскольку для нерелятивистской частицы - волновое число, введенное выше. Полученное дифференциальное уравнение по своей математической форме соответствует уравнению (1.2) гармонических колебаний, решение которого записывается в виде

y(x)= Ccos(kx-a)= , (18.4)
а A и B определяются из граничных условий, согласно которым на левой и на правой границе (при х = 0 и х = L ) частица находиться не может. Поэтому из (18.4) получим y(0)= A×1 + B×0 = 0, откуда А = 0. Второе условие даст y(L)= B sin kL = 0. Если предположить, что и В = 0, то получится, что всегда для любого х волновая функция y(х) º 0, что означает, что частица нигде не находится. Но она есть! Поэтому остается положить, что sin kL = 0, откуда kL = pn,
где n = 1,2,3... - квантовое число (n = 0 опять-таки исключается, чтобы не получить тождественный ноль). Подставляя в последнее соотношение значение k, получим откуда получается выражение для дискретного спектра собственных значений энергии частицы в потенциальной яме (eigenvalues)[1]:

. (18.5)

Вернемся, однако, к волновой функции. Для этого нужно найти В в (18.4). Используем для этого условие нормировки: интеграл по всей длине ямы ò|y(x)|2dx cоответствует вероятности найти там частицу где-нибудь и равен единице (она там, некуда ей деться). Поэтому

, откуда . Получаем спектр собственных функций (eigenfunctions) и плотность вероятности:

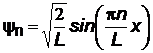; . (18.6)

На рис. 18.3 представлены графики плотностей вероятности вместе с соответствующими энергетическими уровнями. В отличие от несчастной Жучки, у микрочастицы есть предпочтения в местах пребывания, характеризуемые максимумами плотности вероятности. Площадь под любой из этих кривых равна единице и соответствует достоверному событию (частица где-нибудь да находится). Вероятность найти частицу на некотором участке ямы от х1 до х2 равна интегралу (для соответствующей волновой функции). Переход к классическому случаю имеет место, когда n ® ¥. В этом случае при большом количестве осцилляций в пределах от 0 до L квантовая специфика утрачивается, и имеет смысл говорить лишь о среднем значении, равном

,

т. е. все положения частицы равновероятны, т. е. Жучке все равно, в какой части колодца пребывать. Задача о Жучке, однако, не только классическая, но и двумерная (в отличие от рассмотренной подробно квантовой одномерной задачи).

Для двумерной квантовой задачи о потенциальной яме с квадратным дном (0 < x, y < L) получится двухкоординатная волновая функция, зависящая от двух квантовых чисел n1 и n2, а для трехмерной (0 < x, y, z < L) получится трехкоординатная волновая функция, зависящая от трех квантовых чисел n1, n2 и n3:

.

Соответствующий спектр собственных значений имеет вид:

.

Заметим, что рис. 18.1 вполне иллюстрирует двумерную квантовую задачу (если только Жучку заменить микрочастицей), а не трехмерную, поскольку вертикальное направление здесь соответствует потенциальной энергии, а не координате z, как это может показаться.

[1] Международное название этого термина дано с присущим физикам чувством юмора: первая часть слова - по-немецки, вторая - по-английски.