Математическая модель трехмерной геологической среды с разломами для решения прямых и обратных задач геофизики

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ТРЕХМЕРНОЙ ГЕОЛОГИЧЕСКОЙ СРЕДЫ С РАЗЛОМАМИ ДЛЯ РЕШЕНИЯ ПРЯМЫХ И ОБРАТНЫХ ЗАДАЧ ГЕОФИЗИКИ

, ,

Московский инженерно-физический институт (государственный университет, г. Москва, e-mail: maximov@dpt39.mephi.ru)

Mathematical model of 3D geological medium with ruptures for solution of direct and inverse geophysical problems

V. A.Larichev, D. N.Lesonen, G. A.Maximov, E. V.Pod’ychev, A. V.Derov

(Moscow Engineering-Physics Institute (State University), Moscow, e-mail: *****@***ru)

Аннотация

В докладе представлен программный комплекс для моделирования сложных трехмерных геологических структур. Использование параметрических би-сплайнов для аппроксимации произвольно распределенных в пространстве данных при построении отдельной геофизической поверхности совместно с иерархической структурой типа дерева для упорядочения отдельных поверхностей в общей модели и удаления их пересекающихся частей являются оригинальными подходами данной разработки.

Развитая математическая модель построения трехмерных геологических структур с разломами позволяет создавать сложные геологические структуры на основе реальных данных с их трехмерной визуализацией, также как и рассчитывать сейсмические волновые поля в реальных геологических структурах.

Abstract

The software for modeling of complex 3D geological structures is presented in the report. The use of parametric b-spline approximation of arbitrary distributed data to build single geophysical surface together with special tree-hierarchy structure for ordering of separate surfaces in the model and cutting of their intersecting parts are the original approaches of the development.

The developed mathematical model for construction of 3D geological structures with faults allow to build complex geological structures by real data with 3d visualization, as well as make calculations of seismic wave fields in real geological structures.

Современный уровень детальности и точности описания геологических сред, необходимый для поиска и дискриминации перспективных нефтяных и газовых горизонтов, требует использования трехмерных моделей геологических структур для решения как прямой, так и обратной задач сейсмического профилирования. Таким образом, моделирование сложных трехмерных геологических структур с внутренними границами по реальным произвольно распределенным данным для их дальнейшей трехмерной визуализации и расчета волновых полей в таких структурах является актуальной задачей.

Чтобы быть адекватными реальности математические модели сред должны удовлетворять следующим требованиям:

·  Модель должна описывать блочно-однородную (градиентную), преимущественно слоистую структуру с криволинейными границами отдельных блоков, возможно, с их неоднозначной проекцией на горизонтальную плоскость, а также с возможностью внутренних разрывов.

·  Входными данными модели является информация о положении границ структурных элементов (границах геологических слоев и разломов) в виде набора произвольно расположенных в пространстве точек, заданных, возможно, с некоторой погрешностью.

·  Модель должна позволять вычислять свойства среды в любой ее точке, а также такие параметры границ ее структурных элементов, как координаты границ, нормали к ним и локальные кривизны.

·  Модель должна описываться возможно меньшим количеством параметров, зависящем от сложности описываемой структуры.

Предлагаемая модель, удовлетворяющая этим требованиям, может быть представлена как набор трехмерных геологических слоев характеризуемых плотностью, скоростями продольных и поперечных волн, а также, если необходимо, другими параметрами. Эти слои разделены в общем случае неплоскими границами.

Требования к описанию границ раздела слоев в предлагаемом подходе вытекают как из необходимости адекватно описывать реальные геологические структуры, так и с особенностями методов расчета волновых полей в рамках модели. В частности, поскольку для вычисления волновых полей часто используется лучевой метод, границы слоев должны быть гладкими поверхностями с непрерывными производными до второго порядка.

В предлагаемом подходе используется слоистая структура среды, но при этом границы слоев представляют собой в целом гладкие искривленные поверхности с разрывами, в общем случае с неоднозначной проекцией на горизонтальную плоскость. Каждая поверхность строится независимо, по соответствующим ей данным сейсморазведки и скважинным данным, и представляет собой параметрический бикубический сплайн, получаемый как решение вариационной задачи. Это позволяет удовлетворить различным дополнительным условиям, в частности разнообразным граничным условиям. При таком подходе границы и их дифференциальные характеристики описываются аналитически, что является важным преимуществом при решении сейсмических задач.

Заметим, что настоящее время в геофизике бикубические сплайны активно используются для описания поверхностей раздела геологических сред. Разным аспектам такого использования посвящены, например, недавние работы [1-3].

В общем случае, на параметрической сетке параметрический бикубический сплайн может быть представлен, как разложение по B-сплайнам в виде.

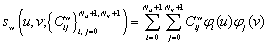(1)

где , а - -ый B-сплайн.

Задача о нахождении совокупности коэффициентов этого сплайна , может быть поставлена как задача минимизации функционала:

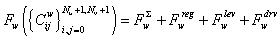(2)

где слагаемое

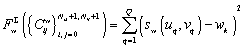(3)

ответственно за прохождение поверхности вблизи точек данных, слагаемое

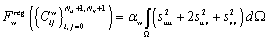(4)

где являющееся линеаризованным функционалом (кривизны) тонкой пластины отвечает за регуляризацию и сглаживание данных, слагаемые

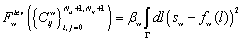
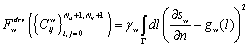(5)

определяет близость краев поверхности к контуру, заданному совокупностью функций , где пробегает по границе области .

Таким образом, при заданной параметризации построение поверхности раздела геологических слоев как параметрического бикубического сплайна сводится к системе линейных уравнений, возникающей из условия :

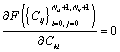(6)

Решение этой системы дает коэффициенты разложения поверхности по бикубическим В-сплайнам, в терминах которых храниться информация о модели.

Обобщение изложенного подхода на нерегулярные параметрические сетки позволяет описывать гладкие поверхности с внутренними разрывами, как показано на рис.1 - рис.3.

Отдельные границы раздела в рамках предлагаемого подхода строятся независимо друг от друга. Чтобы исключить их взаимное пересечение и описать сложные геологические структуры границы упорядочиваются в рамках иерархической модели, которая определяет какие из частей границы реально существуют, а какие должны быть удалены.

Таким образом, не выходя за рамки слоистой топологии, такой подход позволяет описывать весьма сложные геологические структуры, границы которых имеют значительную кривизну, и могут иметь неоднозначную проекцию на горизонтальную плоскость, а также разрывы, сбросы и др.

Для решения различных задач в рамках представленной модели разработан алгоритм, позволяющий определить свойства среды в любой точке как внутри слоя, так и на граничных поверхностях. Разработаны алгоритмы расчета волнового поля в модели в лучевом приближении. В частности, решена задача лучевой трассировки от источника к приемнику, а также задача вычисления волнового поля вдоль лучей.

Все описанные выше алгоритмы включены в разработанный авторами программный комплекс, предназначенный для создания трехмерных моделей геологических структур их трехмерной визуализации, а также для расчета волновых полей в рамках созданных моделей.

Рис 1.

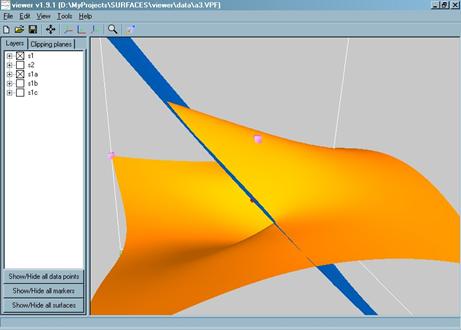
Рис.2

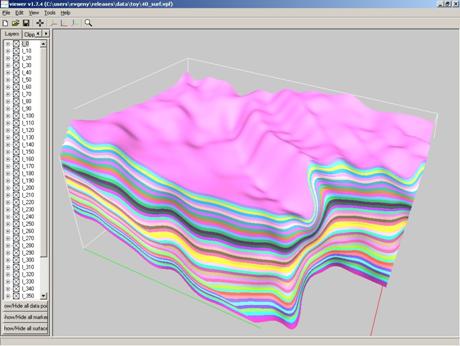
Рис.3

Литература

[1] Apprato D., Gout C., Komatitsch D. A new method for Ck-surface approximation from a set of curves, with application to ship track data in the marianas trench1 // Mathematical Geology 2002, Vol. 34, No. 7, p.831-843.

[2] Billings S. D., Beatsonz R. K., Newsam G. N. Interpolation of geophysical data using continuous global surfaces // Geophysics 2002, Vol. 67, No. 6; p. 1810–1822

[3] Sulebak J. R., Hjelle Ø. Multiresolution Spline Models and Their Applications // Geomorphology Concepts and Modeling in Geomorphology: International Perspectives TERRAPUB, Tokyo, 2003. pp. 221–237.