Третья глава посвящена разработке алгоритма выбора энергооптимального управления движением поезда по перегонам при применении рекуперативного торможения и учете ограничений на фазовую координату.
Алгоритм синтеза энергооптимальной траектории движения поезда реализован на основе численного совместного решения системы дифференциальных уравнений движения поезда и дифференциального уравнения р-функции для удовлетворения необходимых условий оптимальности.
Последовательность решения следующая: при заданной величине скорости ![]() (или однозначно с ней связанной величиной l) путем интегрирования дифференциальных уравнений движения поезда и р-функции при известных граничных условиях v и p строится зависимость
(или однозначно с ней связанной величиной l) путем интегрирования дифференциальных уравнений движения поезда и р-функции при известных граничных условиях v и p строится зависимость ![]() , получается последовательность режимов управления, удовлетворяющая необходимым условиям оптимальности, и определяется время хода. Далее путем итерационной процедуры, изменяя
, получается последовательность режимов управления, удовлетворяющая необходимым условиям оптимальности, и определяется время хода. Далее путем итерационной процедуры, изменяя ![]() , получаем энергооптимальную траекторию, соответствующую заданному времени хода. Для полного определения энергооптимальной траектории необходимо иметь возможность рассчитывать точки переключений оптимальных режимов. Анализ характеристик подвижного состава HR-29 Ханойского метрополитена и уклонов перегонов 1-ой линии метрополитена г. Ханоя позволяет перечислить следующие режимы управления на оптимальной траектории: РК (до 7км/ч), СР, ВБ, С, ТГ, ТМ. Режим ТМ используется при остановке поезда в конце перегона, причем при
, получаем энергооптимальную траекторию, соответствующую заданному времени хода. Для полного определения энергооптимальной траектории необходимо иметь возможность рассчитывать точки переключений оптимальных режимов. Анализ характеристик подвижного состава HR-29 Ханойского метрополитена и уклонов перегонов 1-ой линии метрополитена г. Ханоя позволяет перечислить следующие режимы управления на оптимальной траектории: РК (до 7км/ч), СР, ВБ, С, ТГ, ТМ. Режим ТМ используется при остановке поезда в конце перегона, причем при ![]() км/ч функционирует только механический тормоз.
км/ч функционирует только механический тормоз.
Следует отметить, что начальные условия р-функции для различных режимов зависят от предыдущего режима, ограничения скорости и профиля пути. На основе этого и начальных условий для режимов ВБ, РК или ТГ на оптимальной траектории решаем совместно систему дифференциальных уравнений движения поезда и р-функции в режимах ВБ, РК или ТГ (только при наличии крутого подъема). Если ![]() не достигает значения р* (значение р-функции в точке переключения следующего режима на оптимальной траектории в соответствии с необходимыми условиями оптимальности), то изменяем начальные условия для режимов ВБ, РК или ТГ до тех пор, пока значение p-функции не будет равно р*. При достижении значения р* функции
не достигает значения р* (значение р-функции в точке переключения следующего режима на оптимальной траектории в соответствии с необходимыми условиями оптимальности), то изменяем начальные условия для режимов ВБ, РК или ТГ до тех пор, пока значение p-функции не будет равно р*. При достижении значения р* функции ![]() получим пару точек переключений режимов на оптимальной траектории для рассматриваемого режима (ВБ, РК или ТГ): точка переключения на оптимальной траектории из предыдущего режима в рассматриваемый режим и точка переключения на оптимальной траектории из рассматриваемого режима в следующий режим. Например, при
получим пару точек переключений режимов на оптимальной траектории для рассматриваемого режима (ВБ, РК или ТГ): точка переключения на оптимальной траектории из предыдущего режима в рассматриваемый режим и точка переключения на оптимальной траектории из рассматриваемого режима в следующий режим. Например, при 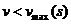 , когда поезд движется в режиме С или ТГ, переход в режиме ВБ происходит при р=1. Если поезд движется в режиме СР или РК, то переход в режиме ВБ происходит при р=h. Аналогично, при
, когда поезд движется в режиме С или ТГ, переход в режиме ВБ происходит при р=1. Если поезд движется в режиме СР или РК, то переход в режиме ВБ происходит при р=h. Аналогично, при ![]() , когда поезд движется в режиме ВБ на оптимальной траектории, при р=1 происходит переход в режим ТГ или С, при р=h переход в режим РК или СР. Рассмотрим следующий случай, когда скорость v>vmax(s) и поезд движется в режиме ВБ. Если поезд движется в режиме ТГ или С, то в начале режима ВБ функция р=1, и р=h если поезд движется в режиме РК или СР. В момент достижения поездом ограничения р-функция изменяется скачком. Увеличение скорости в режиме ВБ возможно только на крутом спуске. Поэтому при достижения ограничения выбирается режим СР, когда продолжается движение на крутом спуске.
, когда поезд движется в режиме ВБ на оптимальной траектории, при р=1 происходит переход в режим ТГ или С, при р=h переход в режим РК или СР. Рассмотрим следующий случай, когда скорость v>vmax(s) и поезд движется в режиме ВБ. Если поезд движется в режиме ТГ или С, то в начале режима ВБ функция р=1, и р=h если поезд движется в режиме РК или СР. В момент достижения поездом ограничения р-функция изменяется скачком. Увеличение скорости в режиме ВБ возможно только на крутом спуске. Поэтому при достижения ограничения выбирается режим СР, когда продолжается движение на крутом спуске.
При переменных ограничениях скорости на перегоне весь перегон разбивается на контрольные фрагменты, границы их совпадают с участками ограничений скорости. Типичные виды контрольных фрагментов показаны на рис. 2. Каждый контрольный фрагмент определяется по трем точкам: начальная точка SV1, конечная точка SV3 и точка SV2.
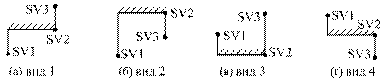
Рис. 2. Основные виды контрольного фрагмента
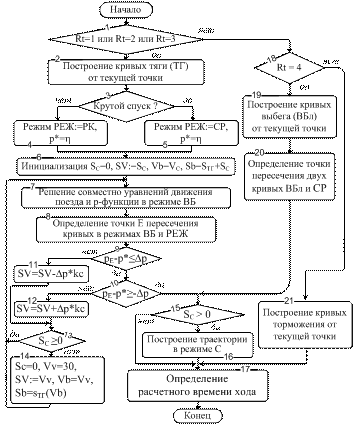
Укрупненная схема алгоритмы синтеза энергооптимальных траекторий представлена на рис. 3. Схема алгоритмов, определяющих работу блоков 6-9, приведены в тексте 3-ей главы. Для иллюстрации в автореферате представлена схема алгоритма при постоянном ограничении скорости, что соответствует блоку 7.
На рис. 4 приведена схема алгоритма построения энергооптимальной траектории для перегонов без крутых спусков и подъемов при постоянном ограничении скорости. С помощью численного интегрирования дифференциального уравнения движения поезда непосредственно от начала точки перегона (точка а на рис. 5) строится траектория в режиме ТГ. Одновременно с этим, начиная от конца перегона (точка b на рис. 5) строится (в обратном направлении) траектория в режиме ТМ до точки, где скорость достигает значения, при котором возможно использование рекуперативного тормоза (v=7 км/ч для метрополитена г. Ханоя), а также строится траектория в режиме РК. Описанный процесс расчета траекторий заканчивается либо при достижении обеими траекториями уровня VС или Vmax, либо до пересечения этих траекторий (этот случай возникает на очень коротких перегонах).
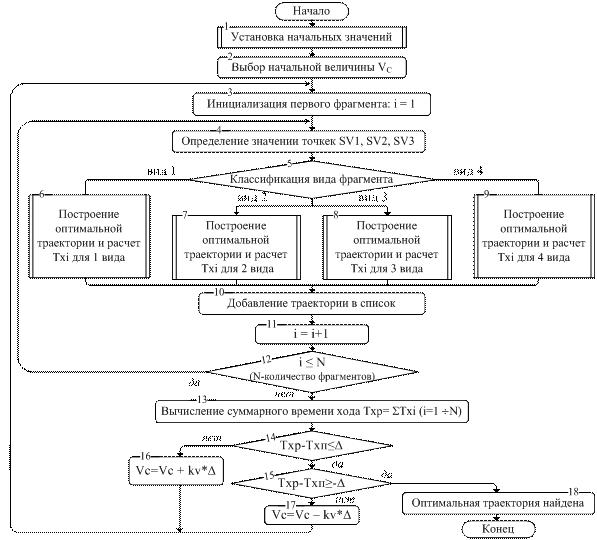
Рис. 3. Алгоритм синтеза энергооптимальных траекторий
На траектории в режиме ТГ (рис. 5.а) при v=30 км/ч задается, начиная от точки m, начальное значение р-функции, равное 1. Решается дифференциальное уравнение р-функции и дифференциальное уравнение движения поезда в режиме ВБ. Расчет р(s) ведется до точки Е (обозначен рЕ), когда v(s) пересекает кривую скорости в режиме РК. Если при этом рЕ=h±Dр (Dр- заданная малая величина), в точке m происходит переход в режим ВБ. В ином случае значение р(0)=1 берем с шагом Dv вправо от точки m и повторяется тот же расчет. Если при некотором iDv (i=1,2…) в точке пересечения скоростей выбега и режима РК значение функции рЕ становится равным h±Dр, это свидетельствует о том, что в точке начала расчета изменяется режим: из ТГ переходим в ВБ на энергооптимальной траектории при фиксированном значении l.
В ином случае, когда в режиме ТГ не выполняется условие перехода на выбег, режим разгона продолжается до скорости VС (рис. 5.б), после чего включается режим С. Начиная от точки k, решается дифференциальное уравнение движения поезда в режиме выбега и дифференциальное уравнение р-функции при начальных условиях р(0)=1. Если в точке пересечения кривых v(s) в режиме ВБ и РК величина рE=h±Dр, то в точке k включается режим ВБ. Если это условие не выполняется, то начальное значение р(0)=1 берется с шагом Ds правее точки k и повторяется тот же расчет. Если при некотором iDs (i=1,2…) в точке пересечения скоростей выбега и режима РК значение функции рЕ=h±Dр, то это свидетельствует о том, что в точке начала расчета изменяется режим: из С переходим в ВБ на энергооптимальной траектории при фиксированном значении l.
Рис. 4. Алгоритм построения энергооптимальной траектории для второго вида ограничения по перегону без крутых спусков и подъемов |
Рис. 5. Зависимости v(s) и p(s) при поиске точек переключения режимов на энергооптимальной траектории |
Схема алгоритма построения энергооптимальной траектории для перегонов с крутыми спусками и подъемами приведена в диссертации.
При наличии крутых спусков на перегоне режимы ВБ, СР на оптимальной траектории могут возникать внутри перегона. Если на перегоне существуют крутые подъемы, то на оптимальной траектории дополнительно может возникать режим ТГ внутри перегона. В процессе поиска точек переключения режимов следует отметить:
- при последовательности режимов ВБ/С-ТГ-С р-функция в режиме ТГ изменяется от начального значения р=1, далее увенчивается до значения, больше 1, потом уменьшается до р=1 в конце режима ТГ (рис. 6.а). В случае, когда скорость поезда в режиме ТГ достигает ограничения скорости (рис. 6.б), р-функция терпит разрыв. Режим ТГ продолжается до того момента, когда скорость поезда достигает VC, при р=1;
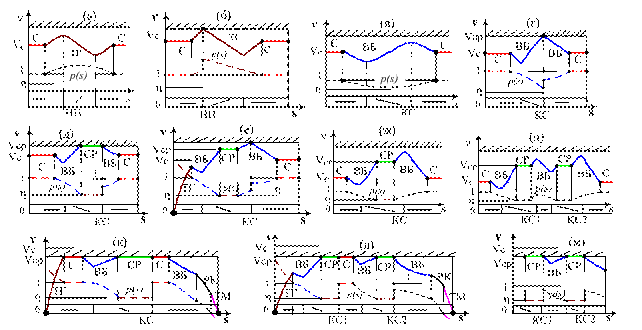
Рис. 6. Зависимость точек переключений режимов от значения р.
- при последовательности режимов ТГ/С-ВБ-С р-функция в режиме ВБ изменяется от начального значения р=1, далее уменьшается до значения, которое должно быть более h, потом увеличивается до р=1 в конце режима ВБ (рис. 6.в). При достижении в режиме ВБ в точке конца крутого спуска (КС) допустимой скорости, р-функция терпит разрыв (рис. 6.г). Режим ВБ продолжается до достижения поездом скорости VC, при p=1;
- при последовательности режимов ТГ/С-ВБ-СР значение р-функции в режиме ВБ изменяется от значения р=1 до р=h в конце режима ВБ (рис. 6.д-л);
- при последовательности режимов РК/СР-ВБ-С р-функция в режиме ВБ увеличивается от значения р=h до р=1 в конце режима ВБ (рис. 6.д-и). При достижении поездом допустимой скорости в режиме ВБ р-функция терпит разрыв в точке КС и траектория ВБ разделяется на два участка: один участок находится левее точки КС, другой участок правее точки КС (рис. 6.д-е);
- при последовательности режимов СР-ВБ-СР р-функция в режиме ВБ изменяется от начального значения р=h, далее увеличивается до значения, больше h и меньше 1, затем уменьшается до р=h в конце режима ВБ (рис. 6.и). При движении поезда в режиме СР с допустимой скоростью р-функция терпит разрыв в точке КС перед началом режима ВБ (рис. 6.м). Этот случай имеет место только на перегоне, в котором более одного крутого спуска.
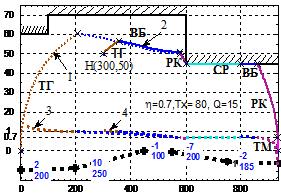
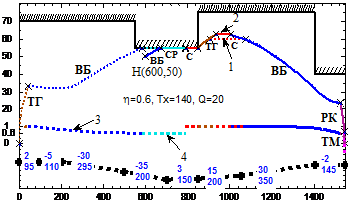
Проведено имитационное моделирование алгоритмов синтеза энергооптимальной траектории на всех 26 перегонах 1-ой линии метрополитена г. Ханоя, из которых на 12 имеются крутые спуски и подъемы. Пример энергооптимальных траекторий приведен на рис. 7. Получены энергооптимальные траектории движения для всех 26 перегонов при изменении времени хода от Тхмин+5с до Тхмин+к5с, где к=1÷6, Тхмин - минимальное время хода. Процесс поиска энергооптимальной траектории для заданного времени хода может состоять из 1-6 итераций. На большинстве перегонов процесс имеет 2-4 итерации.
На перегоне «Maidich-Mydinh» |
На перегоне «Kimma-Catlinh» |
Рис. 7. Энергооптимальные траектории движения поезда метрополитена г. Ханоя:
1- vmax(s); 2- v(s); 3- значение h; 4- значение λ; 5- загрузки поезда, т; 6- заданное время хода, с; 7- расчетное время хода, с; 8- расход электроэнергии на тягу, кВт*ч; 9- общий расход электроэнергии, кВт*ч; 10- p(s); 11- значение уклонов; 12- длина элементов профиля.
В четвертой главе исследовано влияния массы поезда, коэффициента возврата энергии рекуперации в сеть h, вида модели поезда («материальная точка» и «нерастяжимая нить») на энергооптимальную траекторию.
С целью анализа влияния выбора моделей на результат расчета энергооптимальных траекторий были рассмотрены все 26 перегоны 1-ой линии метрополитена г. Ханоя, в том числе 14 перегонов с легким профилем и 12 с тяжелым. Длина рассматриваемых перегонов варьируется от 550м до 1545м. Значения уклонов и подъемов варьируется от -35‰ до 35‰.
По энергооптимальным режимам, полученным для одной модели поезда, выполнялся традиционный тяговый расчет (по заданным режимам) при движении поезда с другой моделью. При заданном времени хода выполнялся энергооптимальный тяговый расчет для обеих моделей.
На перегонах с легким профилем при традиционном тяговом расчете с моделью поезда «материальная точка» по заданным режимам энергооптимального управления, полученного для модели «нерастяжимая нить», максимальная разность мгновенных скоростей не превышает 3%, разность времен хода - 2.5%, разность расхода энергии 2%. Для перегонов с тяжелым профилем разность скоростей достигает 35%, разность времен хода 5%, разность расхода электроэнергии - до 15%. Моделирование показало, что в случае тяжелого профиля определяющим в разности результатов для разных моделей является расчет дополнительного сопротивления при движении поезда на выбеге. Аналогичные результаты получаются при традиционном тяговом расчете с моделью поезда в виде «нерастяжимая нить» по заданным режимам энергооптимального управления, полученного для модели «материальная точка» (см. пример на рис. 8).
|
|
Рис. 8. Траектория движения поезда на перегоне «Caugiay-Kimma» при модели «нерастяжимая нить», рассчитанная по энергооптимальным режимам, полученным на модели «материальная точка»: 1- исходная энергооптимальная траектория, полученная по модели «материальная точка», 2- траектория, рассчитанная по заданным режимам на модели «нерастяжимая нить»; 3, 4- результаты расчета соответственно для траектории 1 и 2; 5, 6- зависимость wg(s) при модели «материальная точка» и «нерастяжимая нить».
Сравнение найденных энергооптимальных траекторий для различных моделей при заданном времени хода на перегонах с легким профилем показало, что максимальное отклонение координат точек переключения режимов не превышает 50м. Разность в расходе электроэнергии при одинаковом времени хода изменяется от 0.2% до 5.5%. Максимальная разность мгновенных скоростей достигает 10%. При расчете на перегонах со сложным профилем установлено, что максимальное отклонение мгновенных скоростей составляет не более 20%, разница в расходе электроэнергии - до 15%. Максимальная разница координат переключения режимов составляет 171м (см. рис. 9).
|
|
Рис. 9. Энергооптимальные траектории движения поезда на перегоне «KimMa-CatLinh» для обеих моделей: 1- при модели «материальная точка», 2- при модели «нерастяжимая нить»; 3, 4- значения энергии соответственно при модели «материальная точка» и «нерастяжимая нить»; 5, 6- зависимость wg(s) при модели «материальная точка» и «нерастяжимая нить».
Итак, использование более простой модели («материальная точка») может привести к недопустимым погрешностям. Модель «нерастяжимая нить» больше согласуется с сущностью физических процессов и рекомендуется для выбора режимов на энергооптимальной траектории.
Рассмотрим далее анализ влияния массы поезда и коэффициента h на энергооптимальную траекторию. Величина коэффициента η непосредственно связана с расходом энергии на тягу поездов. Вместе с тем, открытым остается вопрос как изменяется вид оптимальной траектории, на сколько смещаются координаты переключения режимов в том случае, когда их последовательность при различных значениях η остается неизменной, на каких перегонах изменяется последовательность режимов, на сколько и на каких перегонах изменяется расход энергии, потребляемый поездом в тяговом режиме на оптимальной траектории. Очевидно, что ответы на эти вопросы зависят от заданного времени хода поезда по перегону и его массы. Следующие количественные и качественные показатели будут характеризовать влияние η и массы загрузки Q поезда на вид оптимальной траектории:
- λ(η, Q, Тх) – зависимость l от η, Q при различных временах хода Тх;
- на каких перегонах и в каких случаях изменяется последовательность режимов управления на энергооптимальной траектории в зависимости от η, Q для заданного времени хода Тх;
- величины отклонений координат переключения режимов в зависимости от η, Q для заданного Тх для перегонов, на которых не изменяется последовательность режимов управления на оптимальной траектории;
- АЭТ(η, Q, Тх) – зависимость расхода энергии, затрачиваемого поездом в режиме тяги при движении по перегону от η, Q при различных временах хода Тх;
- АЭ(η, Q, Тх) – зависимость расхода энергии при движении поезда по перегону от η, Q при различных временах хода Тх.
Как показывает анализ плановых графиков движения на метрополитене время хода поездов выбирается в диапазоне Тхмин≤Тх≤Тхмин+30с шагом в 5с. Масса поезда изменяется в диапазоне от массы поезда без пассажиров до массы полностью загруженного поезда в часы пик. При моделировании рассматриваются варианты: 0т, 5т, 8т, 10т, 15т, 20т. Величина коэффициента возврата энергии в режиме рекуперации принимается равной 0.2, 0.4, 0.5, 0.6, 0.7, 0.8.
В результате сравнения энергооптимальных траекторий при заданных временах хода и фиксированной загрузке было установлено, что более чем в 90% случаев последовательность режимов на энергооптимальной траектории не зависит от параметра η. Полученные расчеты позволили также определить зависимости λ и VС от времени хода, загрузки и коэффициента h. Изменение структуры траектории при изменении η происходит в двух случаях. В обоих случаях сравнивались траектории при заданных значениях ТХ, Q.
Первый случай изменения структуры траектории возникает, когда в найденной траектории при заданном η=η1 отсутствует режим стабилизации и происходит переход из режима тяги в режим выбега, а новое значение VС при η=η2 оказывается ниже скорости перехода из тяги в выбег (VТВ), т. е. ![]() . Тогда происходит изменение структуры энергооптимальной траектории - добавляется режим С (рис. 10.а).
. Тогда происходит изменение структуры энергооптимальной траектории - добавляется режим С (рис. 10.а).
(а) - На перегоне «Nhon-Minhkhai» |
(б) - На перегоне «Minhkhai-Phudien» |
Рис. 10. Сравнение траекторий движения при изменении коэффициента η
Второй случай, если для заданных ТХ и Q была определенна такая λ, что соответствующая ей VC>Vmax, то в расчетах VC принимается равной Vmax. Поэтому второй случай изменения траектории возникает, когда присутствует режим С и значение VC при η=η2 оказывается ниже скоростного ограничения Vmax и ниже VC при η=η1, т. е. ![]() и
и ![]() (рис. 10.б). Однако величина перерасхода энергии в этом случае не превышает 5%. При выборе параметра η, равного его математическому ожиданию, перерасход в электроэнергии из-за погрешности задания η не будет превышать 2%.
(рис. 10.б). Однако величина перерасхода энергии в этом случае не превышает 5%. При выборе параметра η, равного его математическому ожиданию, перерасход в электроэнергии из-за погрешности задания η не будет превышать 2%.
Расход энергии увеличивается с увеличением загрузки вагона. При работе авторежима тяговые и тормозные усилия выбираются пропорционально загрузке вагона таким образом, что ускорение и замедление практически не зависит от массы. Сила основного сопротивления движению зависит от массы поезда. Следовательно, основное отличие при различных загрузках в движении поезда будет наблюдаться в режиме выбега. При указанной погрешности авторежима в 2т отклонение координат переключения режимов будет незначительным. Перерасход электроэнергии будет менее 1%. Изменение структуры оптимальной траектории при изменении массы на всех рассматриваемых перегонах не наблюдалось.
В пятой главе разработан алгоритм РВХ для 1-ой линии метрополитена г. Ханоя. Рассматривается РВХ с упреждающим тяговым расчетом. В регуляторе циклически рассчитывается энергооптимальная траектория и в зависимости от результатов расчета вырабатывается управление (см. рис. 11). Алгоритм РВХ основан на циклическом упреждающем тяговом расчет на отрезке пути от текущего состояния поезда до конца перегона. Тяговый расчет циклически повторяется, что позволяет учитывать внешние возмущения, нестабильность основного сопротивления движению, неточность задания исходных заданных и характеристик поезда.
Основной целью алгоритма РВХ является определение точек переключения режимов, при которых движения осуществляется по энергетически оптимальной траектории и выполняется заданное время хода. Алгоритм выбора точек переключения режимов базируется на результатах, полученных в 3-ей главе диссертации при построении энергооптимальных траекторий.

Рис. 11. Блок РВХ в системе САВПМ: FB - возмущающее воздействие;
ИсУ - исполнительное устройство; R - режимы управления
Анализ структур энергооптимальных траекторий и последовательность режимов на всех 26 перегонах метрополитена г. Ханоя позволяет перечислить следующие переключения режимов в зависимости от изменения p-функции: переходы из режимов ТГ или С в режим ВБ, а затем переход из режима ВБ в режим РК или СР осуществляется соответственно при р(s)=1 и р(s)=h. На энергооптимальной траектории основное отличие при различных загрузках в движении поезда будет наблюдаться в режиме ВБ. Следовательно, в ходе определения точек переключений режимов необходим только перерасчет значения р(s) в режиме ВБ.
На рис. 12 представлена схема алгоритма РВХ. Работа главной процедуры в алгоритме РВХ (в блоке 6 на рис. 12) показана рис. 13. Процедура «Расчет на первом фрагменте перегона, содержащем в текущий момент времени координату головы поезда», реализует расчет энергооптимальной траектории и времени движения поездом по этому фрагменту. Режимы ведения поезда на оптимальной траектории по этому фрагменту выбираются следующие:
- если поезд двигается в режиме ТГ (Rt=1), режиме ВБ (Rt=2) или режиме С (Rt=3), то установится дальнейшая последовательность режимов ведения поездом ТГ/С-ВБ-СР/РК;
- если поезд двигается в режиме СР (Rt=4), то дальнейшая последовательность режимов ведения поездом - СР-ВБ-СР;
- если поезд двигается в режиме РК, то дальнейшая последовательность режимов ведения поездом - РК-ТМ.
Проведенное имитационное моделирование показало эффективность разработанного алгоритма РВХ на всех 26 перегонов 1-ой линии метрополитена г. Ханоя (см. пример на рис. 13). Время работы алгоритма РВХ на перегонах с одним ограничением скорости не превышает 10с. Время работы алгоритма РВХ на перегонах с более, чем одним ограничением скорости, не превышает 15с.
|
Рис. 13. Алгоритм РВХ на первом фрагменте |
Для сокращения времени работы алгоритма РВХ на перегонах, имеющих более одного уровня ограничений скорости, используется расчет энергооптимальной траектории на одном фрагменте, содержащем текущую точку. Дальнейшая часть траектории соответствует рассчитанной предварительной энергооптимальной траектории. В этом случае найденная траектория называется квазиоптимальной. Анализ результатов сравнения энергооптимальной и квазиоптимальной траектории показал, что расход электроэнергии не увеличивается более, чем на 2.5%, а время расчета сокращается 1.2÷1.5 раза.
На перегоне «Mydinh-Maidich» |
На перегоне «Kimma-Catlinh» |
Рис. 14. Результаты работы регулирования времени хода: 1- предварительная энергооптимальная траектория при заданном времени хода по перегону; 2- энергооптимальная траектория по перегону от текущей точки Н(sH,vH) до конца перегона; 3, 4- зависимость значения p(s) соответственно траектории 1 и 2.
Выполненные в работе расчеты расхода энергии AЭ при движении поезда по оптимальной траектории позволили получить зависимости AЭi(TХi) для каждого перегона 1-ой линии метрополитена г. Ханоя (i=1,2,..26). Эти данные позволяют решить еще одну оптимизационную задачу для метрополитена г. Ханоя: распределить время хода поездов по 1-ой линии на времена хода по перегонам с целью минимизации расхода энергии. Формальная постановка этой задачи известна: даны зависимости AЭi(TХi) для всех перегонов линии; время хода по линии Туч (без длительностей стоянок, выбираемых из соображении комфорта пассажиров и особенностей управления движением):
где N- число перегонов линии. | (5) |
Расход энергии при движении поезда по линии равен: | (6) |
и является функцией N переменных. Требуется найти минимум функции (6) при условии (5).
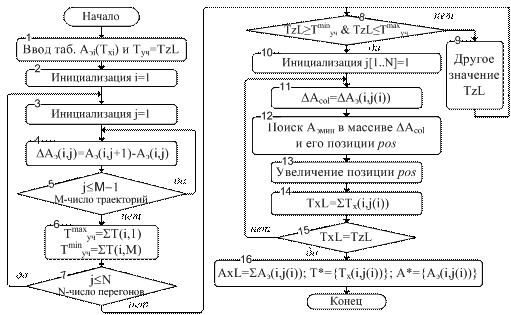
Рис. 15. Блок-схема алгоритма распределения времени хода по 1-ой линии Ханойского метрополитена на времена хода по перегонам.
Учитывая дискретность заданных времен TХi (обычно для метрополитенов шаг составляет 5с), эту задачу поиска условного экстремума, как показали работы, выполненные в МИИТе, удобно реализовать, используя метод динамического программирования. На рис. 15 приведена блок-схема алгоритма распределения участкового времени хода по 1-ой линии Ханойского метрополитена на времена хода по перегонам.
В работе проведено распределение Туч для 1-ой линии метрополитена г. Ханоя для различных зависимостей AЭi(TХi), полученных при детерминированных вариантах h (0, 0.25, 0.5, 0.8) и при задании h для каждого перегона случайным образом по закону равномерной плотности вероятности в диапазоне от 0 до 1. Расход энергии, полученный после оптимального распределения участкового времени хода по линии на времена хода по перегонам, сравнивался с расходом энергии, рассчитанным для времен хода по расписанию (расписание было дано дирекцией метрополитена г. Ханоя). Во всех случаях изменения h при решении оптимизационной задачи дало ощутимый эффект. В частности, средняя по h экономия расхода энергии составляет 2.6%, 2.1%, 2.7%, 2.4% соответственно в часы пик, часы не пик по пути 1 и в часы пик, часы не пик по пути 2 (1-ая линия метрополитена г. Ханоя). Применение рекуперативного торможения позволяет экономить электроэнергию на тягу по сравнению с отсутствием рекуперации на величину до 34.6%, 27.5%, 31.9%, 27.4% соответственно в часы пик, часы не пик по пути 1 и в часы пик, часы не пик по пути 2 (при усреднении по h от 0 до 1).
ЗАКЛЮЧЕНИЕ
В диссертационной работе решена задача, имеющая существенное значение для автоматизации управления движением поездов, заключающаяся в выборе энергооптимального управления для поездов метрополитена г. Ханоя с асинхронными тяговыми двигателями и рекуперативно-реостатным тормозом.
Основные выводы и результаты диссертации:
1. На основе анализа существующих автоматизированных систем управления движением поездов метрополитена в России и в других странах рекомендована на линии строящегося метрополитена г. Ханоя централизованная структура автоматизированной системы управления движением поездов метрополитена, принятая в России.
2. Разработанная имитационная модель движения поездов НR-29 по перегону, учитывающая рекуперативно-реостатный тормоз позволяет решать задачу выбора оптимальных режимов управления движением поезда по критерию минимума расхода энергии на тягу.
3. На основе принципа максимума для поезда с рекуперативно-реостатным тормозом при учете переменных по пути ограничений на фазовую координату разработана процедура выбора режимов управления, обеспечивающая движение поезда по энергооптимальной траектории при фиксированном времени хода.
4. Дифференциальное уравнение р-функции совместно с дифференциальным уравнением движения поезда и граничными условиями образуют полную систему соотношений, позволяющую определить энергооптимальную траекторию. Получена таблица допустимых переключений режимов на энергооптимальной траектории движения поезда при учете рекуперативно-реостатного тормоза и ограничений на фазовую координату.
5. Разработано алгоритмическое и программное обеспечение для выбора энергооптимальных траекторий движения поездов НR-29 для метрополитена г. Ханоя.
6. Проанализировано влияние выбора моделей поезда («материальная точка» и «нерастяжимая нить») на энергооптимальную траекторию. В результате моделирования на всех 26 перегонах 1-ой линии метрополитена г. Ханоя рекомендовано использовать модель поезда «нерастяжимая нить» при выборе энергооптимальных режимов управления. На перегонах со сложным профилем разность координат переключения режимов на оптимальной траектории при модели поезда «материальная точка» от соответствующих координат при модели поезда «нерастяжимая нить» достигает 171м. Разность расходов энергии - 15%.
7. В результате сравнения энергооптимальных траекторий при заданных временах хода и загрузке было установлено, что более чем в 90% случаев последовательность режимов энергооптимальной траектории не зависит от параметра η. Найдены перегоны с крутыми спусками и подъемами, на которых следует учитывать зависимость последовательности переключения режимов на энергооптимальной траектории от h. Оценен перерасход энергии при использовании в регуляторе времени хода величины среднего значения h.
8. Разработан алгоритм работы регулятора времени хода поездов НR-29 для Ханойского метрополитена на базе циклически повторяющегося энергооптимального тягового расчета.
9. Используя метод динамического программирования, для 1-ой линии метрополитена г. Ханоя получено энергооптимальное распределение времени хода по линии на времена хода по перегонам.
ОСНОВНОЕ СОДЕРЖАНИЕ ДИССЕРТАЦИИ ОТРАЖЕНО
В СЛЕДУЮЩИХ ПУБЛИКАЦИЯХ
1. , С., Чинь Лыонг Миен. Энергооптимальное управление движением поезда с рекуперативным тормозом при учете ограничений на фазовую координату// Наука и техника транспорта, 2010, № 4, с.19-29.
2. Чинь Лыонг Миен. Структура АСУ в метрополитене Ханоя// Мир транспорта, 2011, № 4, с.110-112.
3. , С., Чинь Лыонг Миен. Оптимальное управление по критерию минимума энергозатрат поездом метрополитена// Электротехника, 2011, № 8, с.9-14.
4. Чинь Лыонг Миен, Структура системы автоматизированного управления движения поездов метрополитена г. Ханоя (Вьетнам)// Труды VIII международной научно - практической конференции «Trans-mech-art-chem», М.: МИИТ, 2010, с.389-391.
5. , С., Чинь Лыонг Миен. Влияние модели поезда на выбор энергооптимальных режимов управления современных поездов метрополитена// Вестник МИИТа, 2010, выпуск 23, с.27-32.
6. , С., Чинь Лыонг Миен. Управление движением поезда с рекуперативным тормозом при учете ограничений на фазовую координату, доставляющее минимум расхода электроэнергии// Труды XI научно-практической конференции «Безопасность движения поездов», М.: МИИТ, 2010, c. II-7 – II-8.
7. Чинь Лыонг Миен. Алгоритм расчета фрагмента оптимальной траектории в системе автоматизированного управления движением поездов метрополитена// Труды XI научно-практической конференции «Безопасность движения поездов», М.: МИИТ, 2010, c. II-4 – II-5.
8. , С., Чинь Лыонг Миен. Энергоэффективное управления поездом метрополитена с асинхронными двигателями и рекуперативным торможением// Cборник тезисов докладов XII Всемирного электротехнического конгресса (ВЭЛК)», 2011, с.82-83.
9. Чинь Лыонг Миен. Алгоритм регулирования времени хода с упреждающим оптимальным тяговым расчетом в системе автоматизированного управления движением поездов метрополитена г. Ханоя// Труды XII научно-практической конференции «Безопасность движения поездов», М.: МИИТ, 2011
10. Чинь Лыонг Миен. Моделирование процесса движения электропоезда (на вьетнамском языке)// Вестник науки транспорта и коммуникации - Ханой, 2011, № 3, с.108-116.
11. Чинь Лыонг Миен. Рекомендуемая централизованная структура автоматизированной системы управления движением поездов на линии строящегося метрополитена г. Ханоя (на вьетнамском языке)// Автоматизация сегодня, 2010, № 000, с.10-11, с.64.
12. Чинь Лыонг Миен. Методология исследования движения электропоезда (на вьетнамском языке)// Автоматизация сегодня, 2011, № 000, с.12-15.
Чинь Лыонг Миен
Алгоритмы управления временем хода поезда в системе автоматизированного управления движением поездов
метрополитена г. Ханоя
05.13.06 – Автоматизация и управление технологическими процессами и производствами (транспорт)

Подписано к печати ____________ Объем 1,5 п. л. Формат 60х84/16
Тираж 80 экз. Заказ № __________
УПЦ. ГИ. МИИТа (www. *****), ГСП-4, Москва, ул. Образцова, стр.9.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 |





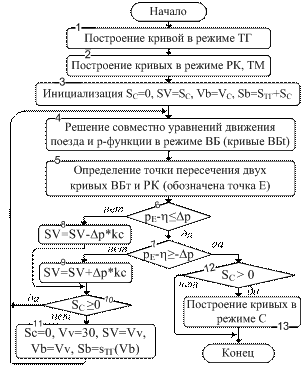
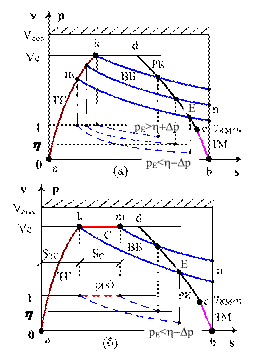
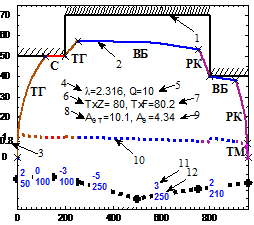
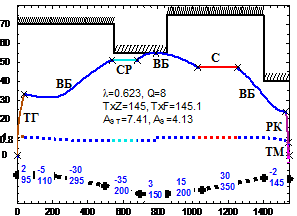
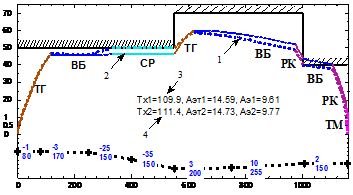
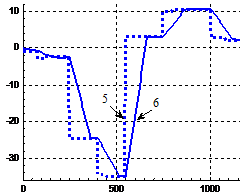
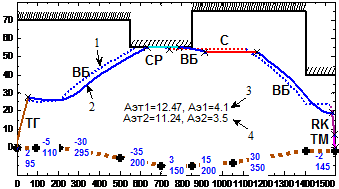
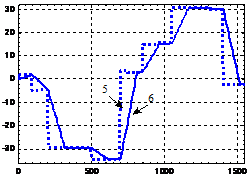
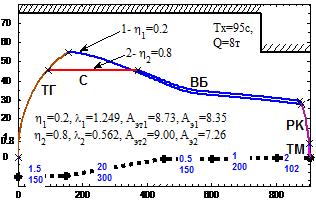
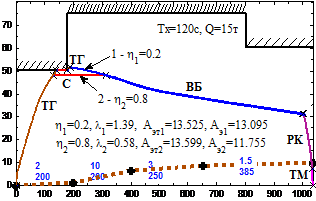
 Рис. 12 . Общий алгоритм РВХ
Рис. 12 . Общий алгоритм РВХ