Равносильные, ТИ и ТЛ формулы алгебры логики. Основные равносильности. (Законы логических операций). Закон двойственности

§4. Равносильные, ТИ и ТЛ формулы алгебры логики. Основные равносильности. (Законы логических операций). Закон двойственности.

Определение.

Две формулы алгебры логики А и В называются РАВНОСИЛЬНЫМИ, если они принимают одинаковые логические значения на любом наборе входящих в формулы элементарных высказываний. Равносильность формул будем обозначать знаком º, а запись А ºВ означает, что формулы А и В равносильны.

Формула А называется ТОЖДЕСТВЕННО ИСТИННОЙ (или ТАВТОЛОГИЕЙ), если она принимает значение 1 при всех значениях входящих в неё переменных.

Формула называется ТОЖДЕСТВЕННО ЛОЖНОЙ (или ПРОТИВОРЕЧИЕМ), если она принимает значение 0 при всех значениях входящих в неё переменных.

Между понятиями равносильности и эквивалентности существует следующая связь: если формулы А и В равносильны, то формула А«В – тавтология, и обратно, если формула А«В – тавтология, то формулы А и В равносильны.

Важнейшие равносильности алгебры логики можно разбить на три группы.

1. Основные равносильности.

законы идемпотентности.

- закон противоречия

- закон исключенного третьего

- закон снятия двойного отрицания

законы поглощения

2. Равносильности, выражающие одни логические операции через другие.

1. 4. .

2. . 5. .

3. . 6. .

Здесь 3, 4, 5, 6 – законы Моргана.

Ясно, что равносильности 5 и 6 получаются из равносильностей 3 и 4, соответственно, если от обеих частей последних взять отрицания и воспользоваться законом снятия двойного отрицания.

Таким образом, в доказательстве нуждаются первые четыре равносильности. Докажем одну из них : первую.

Так как при одинаковых логических значениях x и y истинными являются формулы , то истинной будет и конъюнкция . Следовательно, в этом случае обе части равносильности имеют одинаковые истинные значения.

Пусть теперь x и y имеют различные логические значения. Тогда будут ложными эквивалентность и одна из двух импликаций или . Но при этом будет ложной и конъюнкция .

Таким образом, и в этом случае обе части равносильности имеют одинаковые логические значения.

Аналогично доказываются равносильности 2 и 4.

Из равносительностей этой группы следует, что всякую формулу алгебры логики можно заменить равносильной ей формулой, содержащей только две логические операции: конъюнкцию и отрицание или дизъюнкцию и отрицание.

Дальнейшее исключение логических операций невозможно. Так, если мы будем использовать только конъюнкцию, то уже такая формула как отрицание не может быть выражена с помощью операции конъюнкции.

Однако существуют операции, с помощью которых может быть выражена любая из пяти логических операций, которыми мы пользуемся. Такой операцией является, например, операция “Штрих Шеффера”. Эта операция обозначается символом ½ и определяется следующей таблицей истинности:

3. Равносильности, выражающие основные законы алгебры логики.

1. - коммутативность конъюнкции.

2. - коммутативность дизъюнкции.

3. - ассоциативность конъюнкции.

4. - ассоциативность дизъюнкции.

5. - дистрибутивность конъюнкции относительно

дизъюнкции.

6. 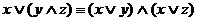- дистрибутивность дизъюнкции относительно

конъюнкции.

4. Дополнительные законы.

1. Закон склеивания (расщепления).

, ;

, .

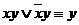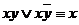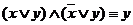2. Законы поглощения.

; .

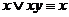3. Закон Блейка- Порецкого.

.

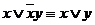4. Закон свертки логического выражения (СЛВ).

.

5. Закон двойственности.

Определение.

Формулы А и А* называются двойственными, если формула А* получается из формулы А путем замены в ней каждой операции на двойственную.

Имеет место следующий закон двойственности: если формулы А и В равносильны, то равносильны и им двойственные формулы, т. е. А* º В*.