Глава 4 Алгебра логики (стр. 1 )

Глава 4 Алгебра логики

В этой главе будем рассматривать практические основы решения логических задач, возникающих при проектировании дискретных устройств. Под дискретными устройствами понимают устройства, осуществляющие переработку информации, представимой в дискретном виде (ЭВМ, устройства управления, системы связи).

Процесс проектирования д. у. можно разделить на 2 части:

1.  Логическое проектирование, т. е. построение функциональной схемы: описание узлов схемы и связей между ними (наша часть задачи).

2.  Техническое проектирование, т. е. построение устройства из физических элементов.

Дискретные устройства делятся на 2 класса:

1.  Комбинационные схемы – устройства, в которых каждому входному сигналу соответствует выходной сигнал.

2.  Последовательностные схемы (схемы с памятью) – устройства, в которых каждому входному сигналу может соответствовать несколько выходных в зависимости от истории работы схемы (т. е. последовательности подаваемых сигналов).

Наиболее удобные методы представления информации в ЭВМ, устройствах управления и автоматизации, широко используют двоичные схемы и двоичную систему счисления. Простая модель, описывающая поведение комбинационных переключательных схем, основана на теории алгебры логики.

4.1  Формулы и функции алгебры логики

4.1.1  Высказывания и операции над ними

Высказыванием называется повествовательное предложение, о котором в данной ситуации можно сказать, что оно истинно либо ложно.

В качестве примеров высказываний можно назвать «Сейчас идет снег» и «Первокурсники СибГУТИ изучают математику».

Если имеется несколько высказываний, то из них с помощью логических связок (логических операций) можно образовывать новые высказывания. При этом исходные высказывания называются простыми, а построенные из них – составными (сложными), например: «Если студент сдаст всю сессию на «отлично», то будет получать повышенную стипендию».

В дальнейшем нас будет интересовать не то, о чем идет речь в данном высказывании (его содержательная часть), а лишь какое значение истинности оно имеет. В алгебре логики все высказывания, имеющие одинаковые значения истинности, взаимозаменяемы, т. е. имеется два класса: класс истинных высказываний и класс ложных высказываний – (И, Л), (T, F), (1,0).

Высказывания a и b являются равносильными (a º b), если совпадают их значения истинности.

Высказыванию Р поставим в соответствие логическую переменную x, которая принимает значение 1, если Р истинно и 0, если оно ложно.

Переменная, которая может принимать только одно из двух значений – 1 или 0, истина или ложь, называется булевой переменной.

Логические операции, или связки: унарная операция – инверсия, бинарные – конъюнкция, дизъюнкция, импликация, равносильность (эквивалентность), штрих Шеффера, стрелка Пирса, кольцевая сумма.

Инверсия (логическое отрицание): NOT, НЕ, , черта над переменной. Меняет значение переменной на противоположное.

Конъюнкция (логическое умножение): AND, И, Ù, ×, &. Имеет значение ложь, если значение хотя бы одного операнда ложно.

Дизъюнкция (логическое сложение): OR, ИЛИ, Ú. Имеет значение истина, если значение хотя бы одного операнда истинно.

Импликация (логическое следование): ЕСЛИ…ТО…, ®. В выражении ЕСЛИ a ТО b переменная a является посылкой (основанием), переменная b – заключением (следствием, выводом). Имеет значение ложь тогда и только тогда, когда из истинной посылки делается ложное заключение.

Равносильность (эквивалентность): …ТОГДА И ТОЛЬКО ТОГДА, КОГДА…, «, ~, º. Имеет значение истина, когда переменные совпадают.

Штрих Шеффера (антиконъюнкция): по определению (a|b) º (a&b).

Стрелка Пирса (антидизъюнкция): (a¯b), по определению (a¯b) º (aÚb).

Кольцевая сумма (сложение по модулю 2, исключающее ИЛИ): по определению (aÅb)º(a«b). Имеет значение истина, когда оба аргумента различны (для большего числа аргументов – когда количество единиц нечетно).

Действия логических операций задаются таблицами истинности, каждой строке которых взаимно однозначно сопоставляется набор значений переменных и соответствующий этому набору результат логической операции. Таблица истинности для основных операций имеет вид:

Введенные операции не являются независимыми, т. е. одни из них могут быть выражены через другие.

Теорема 4.1   

1.  A ® B º ØA Ú B.

2.  A « B º (A ® B)&( B ® A) º (A & B) Ú (ØA & ØB) º (ØA Ú B) & (A Ú ØB).

Доказательство: с помощью таблиц истинности.

4.1.2  Построение формул

Из логических переменных с помощью логических связок можно составлять конструкции, которые образуют формулы алгебры логики.

Пусть {xi | iÎI} – некоторое множество логических переменных. Формулой алгебры логики является любая логическая переменная (атомарной формулой) или выражение, построенное из формул с помощью логических операций.

Данное определение задает синтаксис формул, т. е. формальные законы их построения. Приведенные выше таблицы истинности являются интерпретациями логических операций и задают семантику формул (т. е. придают им смысл).

На основании таблиц истинности для логических операций можно строить Т. И. для произвольных формул.

Любая формула, кроме элементарной, должна быть заключена в наружные круглые скобки. Однако обилие скобок затрудняет чтение формул, поэтому в алгебре логики приняты некоторые соглашения относительно расстановки скобок: 1) внешние скобки не пишутся; 2) знак конъюнкции можно обозначать точкой или не писать; 3) на множестве {, &, Ú, ®, «, |, ¯, Å } вводится приоритет операций, который определяется посредством транзитивного отношения > «быть сильнее» и отношения эквивалентности ~«быть равносильным». Если все равносильные операции объединить в классы эквивалентности {}, то можно записать: {} > {&, |, ¯} > {Ú} > {®} > {«, Å}.

В таком случае скобки в формулах ставятся только тогда, когда требуется изменить последовательность выполнения операций.

  Пример 4.1  ((((a&b)&c)Úd)®((aÚb)&a)) º abc Ú d ® (aÚb)&a, в итоге в формуле осталась только одна пара скобок, которая нужна для того, чтобы дизъюнкция выполнилась прежде конъюнкции. И наоборот, расставим скобки в формуле в соответствии с последовательностью выполнения операций: xÅy«z®uÚv&w¯x|y º ((xÅy)«(z®(uÚ(((v&w)¯x)|y)))).

4.1.3  Булевы функции и формулы

Функцией алгебры логики (ФАЛ) от n переменных x1, x2, …, xn называется функция f:{0,1}n®{0,1}, т. е. функция, которая произвольному набору
(s1, …, sn) нулей и единиц ставит в соответствие значение f(s1, …, sn)Î{0,1}.

ФАЛ называются также булевыми функциями, двоичными функциями или переключательными функциями. Аргументы булевой функции являются булевыми переменными. Булеву функцию можно задать таблицей истинности.

Утверждение Для булевой функции от n аргументов существует 2n различных наборов аргументов.

Булева функция f(x1, x2, …, xn) называется полностью определенной, если ее значения определены на всех 2n наборах переменных. В противном случае функция частично определенная.

Функция 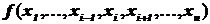существенно зависит от переменной xi, (или переменная xi – существенная), если $ такой набор значений x1, x2, …, xn , что . В противном случае переменная xi – несущественная (фиктивная).

  Пример 4.2  Пусть две булевы функции заданы таблицей истинности. Для них переменная x1 существенная, а x2 – несущественная.

По определению булевы функции равны, если одна из другой получается введением или удалением несущественных переменных.

Одна и та же функция может иметь множество реализаций формулами над данным базисом (т. е. множеством логических операций). Формулы, реализующие одну и ту же функцию, называются равносильными (т. е. на всех наборах переменных их значение истинности совпадает). Отношение равносильности формул является отношением эквивалентности.

Пусть даны формулы F(y1, y2, …, ym ), f1(x1, x2, …, xn ), …, fm(x1, x2, …, xn ). Тогда подстановкой формул fi в формулу F называется следующая конструкция: (F| yi fi )(x1, x2, …, xn) º F(f1(x1, x2, …, xn ), …, fm(x1, x2, …, xn )).

Теорема 4.2  (О подстановке формул)

Если F(y1, y2, …, ym ) и fi (x1, x2, …, xn ) – формулы алгебры логики, то
(F| yi fi )(x1, x2, …, xn ) также является формулой.

Иначе: Вместо некоторой подформулы в формулу может быть подставлена другая формула, и в результате получится правильно построенная формула.

Правило подстановки

Если в равносильных формулах: F(y1, y2, …, ym ) ºG(y1, …, ym ) – вместо всех вхождений некоторой переменной yi подставить одну и ту же формулу, то получатся равносильные формулы.

Правило замены

Если в формуле F заменить некоторую подформулу yi на равносильную gi, то получатся равносильные формулы.

ФАЛ, при образовании которых используются только операции отрицания, конъюнкции и дизъюнкции, называются булевыми формулами.

Теорема 4.3  Для любой формулы алгебры логики существует равносильная ей булева формула.

4.1.4  Булевы функции и булева алгебра

Множество булевых функций с определенными на нем операциями отрицания, конъюнкции и дизъюнкции называется булевой алгеброй. Множество булевых функций от n аргументов будем обозначать Pn.

Для булевой алгебры выполняется ряд равносильностей, которые являются ее аксиомами.

Аксиомы булевой алгебры:

1.  Операции с константами:
1) A Ú 1 º 1; A & 1 º A; 2) A Ú 0 º A; A & 0 º 0.

2.  Противоречие: A & ØA º 0.

3.  Исключение третьего: A Ú ØA º 1.

4.  Идемпотентность: A & A º A; A Ú A º A.

5.  Двойное отрицание: Ø ØA º A.

6.  Коммутативность: A & B º B & A; A Ú B º B Ú A.

7.  Ассоциативность:
(AÚB)ÚC º AÚ(BÚC); (A&B)&C º A&(B&C).

8.  Дистрибутивность:
A & (B Ú C) º (A & B) Ú (A & C); A Ú (B & C) º (A Ú B) & (A Ú C).

9.  Законы де Моргана: Ø(A&B) º ØA Ú ØB; Ø(AÚB) º ØA & ØB.

Используя приведенные аксиомы, возможно выполнять равносильные преобразования, выводить и доказывать новые законы. В частности, при выполнении преобразований часто используются законы поглощения:
1) A & (A Ú B) º A; A Ú A & B º A;
2) ØA & (A Ú B) º ØA & B; A Ú ØA & B º A Ú B.

Эти законы несложно доказать с помощью аксиом.

4.1.5  Принцип двойственности

Пусть f(x1, x2, …, xn ) – булева функция. Двойственной к ней называется функция f*(x1, x2, …, xn ) º f (`x1,`x2, …,`xn ). Из определения видно, что двойственность инволютивна: f**=f.

Если двойственная функция f* совпадает с исходной функцией f, то такая функция f называется самодвойственной.

  Пример 4.3  (0)* º`0º1; (x)*= (`x) º x Þ Функция, тождественно равная своему аргументу, является самодвойственной.

Теорема 4.4  (Общий принцип двойственности)

Если G(x1, …, xn ) получена подстановкой fi из F(y1, …, ym ):
G(x1, …, xn )º (F| yi fi )(x1, …, xn ), то G*(x1, …, xn )º (F*| yi f*i )(x1, …, xn ).

Теорема 4.5  (Принцип двойственности для булевых функций)

Двойственная к булевой функции может быть получена заменой констант 0 на 1, 1 на 0, дизъюнкции на конъюнкцию, конъюнкции на дизъюнкцию и сохранением структуры формулы (т. е. соответствующего исходному порядка действий).

  Пример 4.4  (x`y Ú z)* º (xÚ`y) & z., (xÚy)* º x&y Þ в таблице истинности значения функции и переменных меняются на противоположные

4.1.6  Алгебра Жегалкина

Булевы функции с операциями умножения и сложения по модулю 2 образуют алгебру Жегалкина.

Аксиомы алгебры Жегалкина:

1.  Операции с константами: A×1 º A; A×0 º 0; A Å 0 º A.

2.  Идемпотентность: A×A º A; A Å A º 0.

3.  Коммутативность: A×B º B×A; A Å B º B Å A.

4.  Ассоциативность: (A Å B) Å C º AÅ (B Å C); (A×B)×C º A×(B×C).

5.  Дистрибутивность: A×(B Å C) º A×B Å A×C.

Можно перейти от алгебры Буля к алгебре Жегалкина, используя следующие соотношения: A Å 1 º`A; AÚB=A Å B Å A×B.

И наоборот, от алгебры Жегалкина к алгебре Буля: A Å B =`A×BÚ A×`B

  Пример 4.5  Перейти к выражению булевой алгебры: (x Å 1)×yÅ (x Å 1) = `x×y Å`x = `xy×`x Ú x×`xy = (x Ú`y)×`x Ú 0 =`x`y.

4.1.7  Контрольные вопросы

1.  Какие высказывания являются равносильными? Приведите пример.

2.  Какие существуют логические операции?

3.  Какие логические операции дают в результате их применения к двум аргументам только одно истинное (ложное) значение? На каких наборах переменных достигается это значение?

4.  Какие операции на всех наборах значений переменных имеют взаимно противоположные значения?

5.  Какие существуют формулы, позволяющие выразить одну операцию через другую?

6.  Каков порядок логических операции в соответствии с их приоритетом?

7.  Что такое переключательная функция?

8.  Сколько существует различных наборов аргументов для функции 5 переменных?

9.  Какая функция является полностью определенной?

10.  Что такое булева алгебра? Что представляют собой аксиомы?

11.  Какая функция является самодвойственной?

12.  В чем состоит принцип двойственности для булевых функций?

13.  Какие операции определяют алгебру Жегалкина?

14.  Как связаны алгебры Буля и Жегалкина?

4.2  Способы представления булевых функций

4.2.1  Нормальные формы

Табличный способ определения истинности сложного выражения имеет ограниченное применение, т. к. с увеличением числа логических переменных число вариантов становится слишком большим. Тогда может быть использован способ приведения формул к нормальной форме.

Аналитическое выражение функции (или формула) находится в нормальной форме, если в ней отсутствуют знаки эквивалентности, импликации, двойного отрицания, а знаки отрицания находятся только при переменных.

Элементарной дизъюнкцией (произведением) называется дизъюнкция (произведение) переменных или их отрицаний, в котором каждая переменная встречается только один раз.

Из за большого объема этот материал размещен на нескольких страницах: 1 2