Электричество. Магнетизм

Московский государственный областной университет

Р. В. МИТИН

КОНСПЕКТ ЛЕКЦИЙ

ЭЛЕКТРИЧЕСТВО

МАГНЕТИЗМ

МОСКВА 2005

Конспект составлен на основе курса лекций, читаемого автором в течение ряда лет для студентов нефизических специальностей. Использованы компьютерные программы: текстовый редактор Word (2000), редактор формул Ms Equation, графический редактор Paint, сложные рисунки и фотографии учёных взяты из Интернета.

© Автор текста и компьютерного оформления – профессор, доктор физ.-мат. наук , МГОУ, кафедра общей физики, 2005 г.

ЭЛЕКТРИЧЕСКОЕ ПОЛЕ

Введение

Ещё более 2,5 тысяч лет тому назад было замечено, что янтарь, потёртый о шерстяную ткань, начинает притягивать к себе лёгкие предметы. Янтарь в переводе на греческий язык это электрон. Отсюда и возникло современное название электричества. За прошедшие 2,5 тысячи лет, а особенно за последние столетия изучением электричества занимались очень многие учёные.

Перейдём к изложению того, что известно об электричестве в настоящее время. Известно же следующее:

1) Существуют два рода электрических зарядов – положительные и отрицательные. Разноимённо заряженные тела притягиваются, а одноимённо заряженные – отталкиваются друг от друга. Разделы учения об электричестве, в которых изучаются свойства неподвижных электрических зарядов, принято называть электростатикой.

2) Электрический заряд любого тела состоит из целого числа элементарных зарядов, равных 1,6 ∙10 -19 кулон. Наименьшей по массе частицей, имеющей отрицательный элементарный заряд, является электрон, соответственно положительно заряженной частицей с такой же массой является позитрон. Кроме того, существует частица с положительным элементарным зарядом примерно в 2000 раз тяжелее электрона – это протон. Электроны и протоны входят в состав атомов всех химических элементов.

3) Закон сохранения электрических заряда – алгебраическая сумма зарядов изолированного тела не изменяется при любых процессах. Итак, заряды не исчезают и не возникают. Этот закон является одним из фундаментальных законов сохранения подобно законам сохранения энергии и импульса.

4) При трении электрически нейтральных тел заряды переходят от одного тела к другому и тела заряжаются разноимённо. Кроме того возможна электризация тела наведением. Что это такое, можно понять, рассматривая результат следующего опыта:

а) – тело нейтральное, б) его разрезали на две части, к которым поднесли заряженное + тело, произошло наведение + и – зарядов, в) развели половинки тела, на каждой половине свой заряд, г) соединили разрезанные половины вместе, суммарный заряд исчез (= 0).

И, наконец:

5) Все вещества можно по способности проводить электрический ток примерно разделить на 3 группы: проводники, диэлектрики, полупроводники.

Взаимодействие зарядов. Закон Кулона.

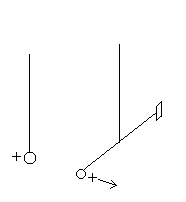
В конце 18 века французский физик Кулон с помощью изобретённых им крутильных весов впервые измерил силу взаимодействия двух заряженных шариков. Что такое крутильные весы, можно понять из рисунка.

Ш. Кулон

В результате этих опытов Кулон установил, что сила взаимодействия двух точечных зарядов

f = k

q1 , q2 – величины зарядов, k – коэффициент пропорциональности, r – расстояние между шариками, точечный заряд – это заряженное тело, размерами которого можно пренебречь по сравнению с расстоянием до других заряженных тел.

Формулировка закона Кулона:

Сила электростатического взаимодействия между двумя точечными зарядами прямо пропорциональна произведению величин зарядов, обратно пропорциональна квадрату расстояния между зарядами и направлена вдоль соединяющей их прямой.

Закон Кулона можно написать в векторном виде:

= k

В системе единиц СИ коэффициент k в законе Кулона имеет вид k = , где ε0 – так называемая электрическая постоянная, которая определяется из опытов и равна ε0 = 8,85 10-12 фар/м

Таким образом, для вакуума закон Кулона имеет вид:

f =

В случае же помещения зарядов в диэлектрическую среду (жидкую, твёрдую, газообразную) сила Кулона ослабляется в ε раз, где ε ­ – относительная диэлектрическая проницаемость среды.

f =

Для воздуха очень близка к единице, а для воды, например, ε = 81, то есть сила Кулона в воде резко ослабевает.

Закон Кулона по форме записи аналогичен закону всемирного тяготения Ньютона. Однако силы тяготения значительно слабее по сравнению с электрическими силами. Пример: внутри атома водорода электрон связан с протоном, то есть с ядром атома как электрическими, так и гравитационными силами. Отношение этих сил составляет fэл / fгр = 2,3 1039 . Почему же мы в обыденной жизни не наблюдаем этих гигантских электрических сил? Только потому, что в каждом отдельном теле + и – заряды практически совершенно точно компенсируют друг друга. Пример: если бы в вашем теле и теле вашего соседа была разница в количестве электронов всего на 1 % , то силы отталкивания между вами хватило бы, чтобы поднять вес, равный весу нашей Земли.

Электрическое поле. Напряжённость поля.

Силовые поля – это одна из форм материи, и физика также изучает эту форму материи. Примером силового поля является гравитационное поле. Кулоновское же взаимодействие между зарядами осуществляется посредством создаваемого ими электростатического поля. Итак, вокруг каждого заряда (и заряженного тела) существует электрическое поле, которое и вызывает действие Кулоновской силы на каждый другой заряд, помещённый в это поле.

Согласно закону Кулона на точечный пробный заряд действует сила от другого точечного заряда f = qпр ( )

Величину, стоящую в скобках принято называть напряжённостью электрического поля, это вектор. Итак, E =

И тогда f = qпр E – сила, действующая на пробный заряд. Согласно этой формуле заряд в один кулон создаёт в пустоте на расстоянии 1 м напряжённость поля, равную 9 ∙ 109 в/м.

Суперпозиция электрических полей

Из опытов следует, что: напряжённость поля системы зарядов равна векторной сумме напряжённостей полей, которые создавал бы каждый из зарядов в отдельности. E = Ei

Линии напряжённости. Поток вектора напряжённости

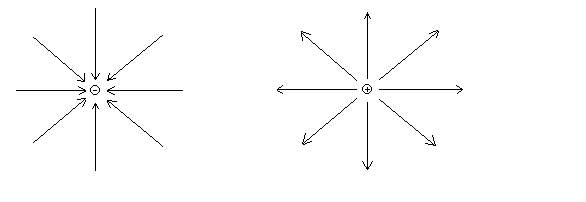
Для графического изображения электрических полей применяется метод силовых линий, или линий напряжённости. Эти линии проводятся таким образом, чтобы касательная к ним в каждой точке совпадала с направлением вектора E . Линии напряжённости не пересекаются, так как в каждой точке вектор E , конечно, имеет лишь одно направление.

Направление линий принято считать от + к – . Густота линий выбирается так, чтобы количество линий, пронизывающих единичную площадь, перпендикулярную к линиям, было равно численному значению вектора E то есть E. Тогда для уединённых – и + зарядов линии напряжённости – прямые и направлены, как показано на рисунке.

Сколько линий нужно нарисовать, то есть чему равно полное число линий N? Мы знаем, что E = , а это и есть густота линий при данном значении r, значит, полное число линий будет равно:

N = E 4 π r2 = 4 π r2 = q / ε0 .

На следующем рисунке представлена картина силовых линий для случая двух разноимённых зарядов (диполь).

Через площадку dS, перпендикулярную к направлению силовых линий проходит E dS линий. Если же dS ориентирована так, что нормаль к ней образует с вектором E угол α , то число линий E dS Cos α . Это ясно из следующего рисунка.

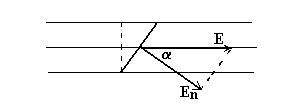
Или мы можем написать, что число линий E dS Cos α = En dS, где En – составляющая вектора E по направлению нормали к площадке dS.

Теперь для произвольной поверхности имеем, что число линий, которые её пронизывают, будет Φ = - интеграл по поверхности. Эта величина называется потоком вектора E через поверхность S. Для сферической поверхности, охватывающей заряд q, получаем Φ = = E 4 π r2 = 4 π r2 = q / ε0 = N. То есть поток равен полному числу силовых линий.

Отметим, что силовые линии не совпадают с траекториями движения лёгких заряженных частиц, находящихся в электрическом поле. По касательной к силовой линии направлена только сила, действующая на частицу, то есть f = q E . Для аналогии рассмотрим движение камня в гравитационном поле Земли.

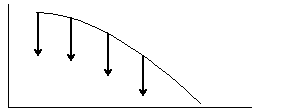
То есть, камень движется по параболе, а сила тяжести направлена вниз (по касательным к силовым линиям гравитационного поля). Точно так же будет и для движения заряженных частиц в электрическом поле.

Теорема Гаусса

Можно показать, что не только для сферической, но и для любой поверхности, охватывающей заряд q, поток вектора также равен q / ε0. И более того, если внутри замкнутой произвольной поверхности находится системе зарядов qi, то поток Φ через эту поверхность равен:

Ф =

Это следует из принципа суперпозиции электрических полей. Итак, мы можем написать окончательно:

Φ =

Это и есть теорема Гаусса, которая звучит так:

Поток вектора напряжённости электрического поля через замкнутую поверхность равен алгебраической сумме заключённых внутри этой поверхности зарядов, делённой на ε0.

Если внутри поверхности заряд распределён непрерывно с объёмной плотностью, зависящей от координат, то теорема Гаусса запишется так:

=

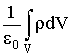
где ρ = lim – объёмная плотность заряда.

Зачем нужна теорема Гаусса? Для того, чтобы сравнительно просто и быстро находить величину напряжённости E.

Примеры:

1) Поле бесконечной заряженной плоскости.

К. Гаусс

Здесь σ = lim

σ – поверхностная плотность заряда. Из соображений симметрии вытекает, что электрическое поле пластины будет направлено таким образом:

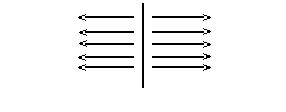
Найдём величину этого поля, используя теорему Гаусса. Рассмотрим цилиндр, опирающийся на элементарную площадку dS, как показано на рисунке. Поток через боковую поверхность цилиндра очевидно равен нулю. А через торцы поток равен 2 E dS, по теореме Гаусса этот поток равен q/ε0 = σ dS/ ε0 отсюда E = σ / 2ε0 .

Полученный результат не зависит от длины цилиндра. Значит, поле Е во всех точках пространства будет одинаково по абсолютной величине.

2) Поле двух разноимённо заряженных плоскостей.

Имеем две плоскости, каждая плоскость создаёт вокруг себя поле, с указанным направлением силовых линий. Абсолютная величина поля E = σ / 2ε0 . Отсюда из принципа суперпозиции полей сразу получим – всё поле сосредоточено только между плоскостями, а его величина E = 2σ / 2ε0 = σ / ε0 .

Работа сил электростатического поля

Кулоновские силы являются центральными, то есть действуют по прямой, проходящей через центры зарядов. Любое центральное поле сил является потенциальным. Это значит, что работа сил поля не зависит от пути перемещения тела в этом поле, а зависит лишь от начального и конечного положения тела. Из этого вытекает, что работа потенциальных сил на замкнутом пути равна нулю.

Вычислим работу при перемещении заряда в электростатическом поле. Пусть мы имеем заряд q, в поле которого движется заряд q′. Работа на элементарном пути равна

dA = f dℓ Cos α = dℓ Cos α

но dℓ Cos α = dr – приращение радиуса–вектора, тогда

dA = dr

для работы на пути 1 - 2 получим:

A12 = = =

Таким образом, работа действительно не зависит от пути, так как в окончательное выражение входят только r1 и r2. Из этой формулы также видно, что работа на замкнутом пути равна нулю. Выражение для работы на замкнутом пути может быть представлено в виде:

dA = f dℓ Cos α = q′ E dℓ Cos α = q′ Eℓ dℓ

где Eℓ = E Cos α – проекция вектора Е на направление перемещения.

Отсюда получим: Eℓ dℓ = 0 для любого замкнутого контура. Это выражение называется циркуляцией вектора Е по замкнутому контуру. Таким образом, циркуляция вектора напряжённости электростатического поля равна нулю.

Потенциал

Напишем снова выражение для работы сил поля на пути 1 – 2.

A12 =

Введём теперь следующую функцию W (r) = . Тогда мы можем написать A12 = W1 – W2 . Вспоминая соотношения механики, мы приходим к выводу, что функция W(r) должна рассматриваться, как потенциальная энергия взаимодействия зарядов q и q′, а работа совершается за счёт изменения потенциальной энергии.

Определим теперь, что такое потенциал. Потенциалом называется отношение φ = W/q′ , то есть функция, зависящая от положения пробного заряда q′, но уже не зависящая от его величины.

Таким образом φ = – это и есть выражение для потенциала поля точечного заряда q.

Из предыдущих формул тогда следует, что заряд q′, находящийся в точке поля с потенциалом φ, обладает потенциальной энергией q′ φ .

Работа же сил поля над зарядом q′ может быть выражена через разность потенциалов A12 = W1 – W2 = q′ (φ1 – φ2) . Если заряд q′ из точки с потенциалом φ1 удалить на бесконечность (то есть φ2 = 0), то A∞ = q′ φ1 Из этого соотношения следует следующее определение потенциала:

Потенциал численно равен работе, которую совершают силы поля над единичным положительным зарядом при его удалении из данной точки на бесконечность.

Связь между напряжённостью электрического поля

и потенциалом

Выразим работу сил поля при перемещении заряда в поле двумя способами: 1) dA = fℓ dℓ = q′ Eℓ dℓ – проекция силы на направление перемещения умножить на элементарное перемещение. 2) dA = – dW (убыль потенциальной энергии), то есть

dA = – dW = – d(q′φ) = – q′dφ = = – q′ dℓ . Сравнивая эти выражения, видим

Eℓ =

Для более общего, трёхмерного случая получим

Ex = – Ey = – Ez = –

И следовательно вектор E = – grad φ

Итак, вектор напряжённости электрического поля равен минус градиенту потенциала. Потенциал, таким образом, является скалярной величиной.

Рассмотрим примеры применения полученной формулы.

1) Потенциал и поле точечного заряда. Для этого случая:

E = – (grad φ)r = – = – =

Мы только что получали формулу φ = .

Значит = = –

Следовательно, E = – =

Напомним, что эту формулу мы уже знаем, сейчас мы её получили, используя формулу для градиента потенциала.

2) Потенциал и поле двух параллельных плоскостей.

Мы с вами уже знаем, что поле внутри таких плоскостей одинаково во всех точках.

E = – следовательно dφ = – E dx и φ(x) = Const – E x

x = 0 φ = φ1 φ1 = Const

x = d φ = φ2 φ2 = φ1 – E d значит

E = φ(x) = φ1 – E x = φ1 – x

Эквипотенциальные поверхности

Для наглядного изображения поля кроме силовых линий применяют метод эквипотенциальных поверхностей.

Эквипотенциальная поверхность это поверхность, все точки которой имеют одинаковый потенциал. Как они проходят? Рассмотрим опять предыдущие два примера.

1) Поле точечного заряда. Из предыдущих формул ясно, что эти поверхности – концентрические сферы с центром в месте расположения заряда. Проведём здесь же силовые линии.

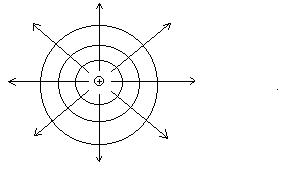
Мы видим, что силовые линии в каждой точке ортогональны (перпендикулярны) эквипотенциальным поверхностям.

2) Две параллельные плоскости. Из предыдущего ясно, что картина должна быть вот такой:

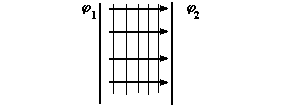
Приведём ещё рисунок для поля диполя и поля двух расположенных рядом положительных зарядов.

Электрическое поле в диэлектрике

Мы знаем, что электрическое поле в среде (диэлектрике) уменьшается в ε раз по сравнению с полем в вакууме. Здесь ε – относительная диэлектрическая проницаемость вещества. Для объяснения этого нам понадобится понятие электрического диполя, то есть + и – зарядов, находящихся на расстоянии ℓ друг от друга. Дело в том, что каждую молекулу среды можно рассматривать, как электрический диполь, имеющий дипольный момент p = q ℓ . При этом могут быть два случая: либо молекула с самого начала обладает дипольным моментом (полярные молекулы), либо дипольный момент наводится в молекуле при её помещении в электрическое поле. (Так как положительные заряды молекулы стремятся сдвинуться по направлению, а отрицательные заряды – против поля).

Если поместить электрический диполь в электрическое поле, то на него будут действовать электрические силы (пара сил), стремящиеся повернуть диполь и установить его вдоль направления поля.

На рисунке приведена схема действия этой пары сил на диполь.

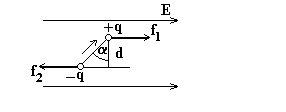
Плечо пары сил d = ℓ Sin α , модуль каждой силы равен q E. Отсюда момент пары сил равен M = q E ℓ Sin α = p E Sin α . ( p = q ℓ )

Или в векторном виде M = [ p E ] .

В отсутствии внешнего электрического поля дипольные моменты молекул диэлектрика или равны нулю (неполярные молекулы), или распределены по направлениям хаотически (полярные молекулы). Под действием внешнего поля диэлектрик поляризуется, результирующий электрический момент становится отличным от нуля. Суммарный электрический момент единицы объёма можно определить так:

P = Определённый таким образом вектор называется вектором поляризации диэлектрика. Из опытов следует, что выполняется следующее соотношение P = κ ε0 E , где κ – диэлектрическая восприимчивость диэлектрика, ε0 – электрическая постоянная.

Легко понять, что при помещении пластины диэлектрика в поле Е поляризация пластины сопровождается появлением на её поверхностях зарядов, так как под действием поля заряды одного знак уходят внутрь, а другого знака выступают на поверхность (внутри диэлектрика эти заряды компенсируют друг друга). Эти заряды называют связанными электрическими зарядами.

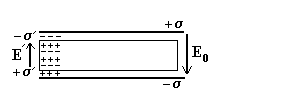
Как видно, связанные заряды создают поле Е′ , направленное против поля Е0 . Теперь мы поняли, почему же в диэлектрике происходит ослабление поля. Мы уже говорили, что ослабление происходит в ε раз. ( Е = Е0 / ε ) . Перейдём теперь к определению величины ε .

Для удобства расчётов электрических полей вводят векторную величину, которая называется электрическим смещением (или электрической индукцией). Эта величина определяется соотношением

D = ε0 E + P . Подставим сюда выражение для P :

D = ε0 E + κ ε0 E = ε0 (1 + κ) E

Величину ε = 1 + κ называют относительной диэлектрической проницаемостью. Теперь получим: D = εε0E .

Можно показать, что теорема Гаусса теперь приобретает вид:

=

то есть выглядит одинаково и для вакуума и для диэлектрика. Формулы для напряжённости поля заряда и потенциала выглядят так

E = φ =

Проводники в электрическом поле

Долгое время считалось, что электризоваться при трении могут только диэлектрики. Только в начале 19 века русским учёным Петровым было на опыте доказано, что и металлы можно электризовать трением, хотя это и трудно сделать. Почему это трудно, теперь понятно, так как металлы – это проводники, и поэтому заряды, созданные при трении не остаются на месте, а быстро распределяются по всему металлу и по другим телам, с ним соединённым. Поэтому современное определение проводников звучит так – проводники это тела, в которых электрические заряды способны перемещаться под действием сколь угодно слабого электрического поля. Заряды, созданные на проводнике сами создают эти слабые электрические поля и начинают отталкиваться друг от друга, в результате они растекаются в конечном результате по поверхности проводника. При этом будут выполняться два условия: 1) Е = 0 во всех точках внутри проводника. Так как E = – grad φ , это означает, что внутри проводника φ = Const. 2) Напряжённость поля на поверхности проводника направлена в каждой точке по нормали к поверхности.

Таким образом, поверхность проводника является эквипотенциальной поверхностью.

Чтобы вычислить Е вблизи поверхности проводника, применим теорему Гаусса. Вырежем мысленно элементарный цилиндр с основанием dS и боковыми стенками, параллельными Е. (При рассмотрении рисунка нужно иметь в виду, что высота такого элементарного цилиндра предполагается очень малой, поэтому верхний и нижний торец имеют одинаковую площадь, равную dS ).

Тогда поток вектора D через всю поверхность цилиндра (верхний торец, боковая, нижний торец) равен:

D dS + 0 + 0 ∙ dS = σ dS (σ – плотность зарядов на поверхности проводника, σ dS – полное число зарядов внутри цилиндра).

Так как D = ε ε0 E то E =

Наибольшая поверхностная плотность зарядов, так же как и величина Е находятся на остриях проводника.

Электроёмкость

Рассмотрим уединённый проводник, которому сообщён заряд. Мы знаем, что заряд распределён по поверхности так, чтобы Е = 0 внутри проводника.

Потенциал в какой то точке вне проводника будет равен φ = . Если мы добавим ещё заряд в n раз больший, чем первоначальный заряд, то он растечётся также по проводнику. В соответствии с этой формулой потенциал в точке возрастёт пропорционально изменению заряда на проводнике. Значит мы можем написать q = C φ, где С – коэффициент пропорциональности для нашего случая. Величину С называют электроёмкостью. Значит C = q / φ , ёмкость проводника численно равна заряду, который повышает потенциал проводника на единицу потенциала (на 1 вольт). Единицей ёмкости является фарада – то есть ёмкость такого проводника, потенциал которого изменяется на 1 вольт при сообщении ему заряда в 1 кулон.

Найдём ёмкость шара. Мы знаем, что для уединённого заряда φ = . Можно показать, что эта же формула выполняется и для потенциала, создаваемого заряженным шаром радиуса R.

Значит ёмкость шара C = q / φ = 4π ε ε0 R. В соответствие с этой формулой ёмкостью в одну фараду обладает шар радиусом 9∙109 м, то есть в 1500 раз больше радиуса Земли.

Конденсаторы

Ёмкость уединённых проводников невелика. На практике же очень часто бывает необходимо запасти как можно больший заряд при небольших размерах используемых проводников. Для этой цели используют устройства, называемые конденсаторами. Два главных свойства конденсаторов.

1) Их ёмкость велика, так как в их конструкции используется близко расположенные друг к другу проводники, в этом случае ёмкость значительно возрастает.

2) Электрическое поле в конденсаторах сосредоточено только внутри них, снаружи практически никакого поля нет.

Рассмотрим ёмкость плоского конденсатора.

Это две пластины на расстоянии d друг от друга, площадью S, находящиеся под потенциалами φ1 и φ2 . Для ёмкости конденсатора имеем C = 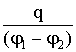. Поле Е связано с σ формулой, которую мы уже знаем – E = = (так как q = σ S ) . Кроме того мы уже получали формулу φ1 – φ2 = E d. Значит φ1 – φ2 = 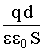. Отсюда: C = ε ε0 S / d

Итак, для увеличения ёмкости плоского конденсатора нужно уменьшать расстояние между пластинами, применять в качестве вещества между пластинами диэлектрик с большим значением ε , и взять побольше общую площадь пластин. На практике конденсаторы изготовляются обычно так: берут две тонкие длинные ленты из металлической фольги (станиоля), между ними тонкая парафинированная бумага или полиэтиленовая плёнка. После этого такой «бутерброд» складывают гармошкой или скручивают. Получается небольшая по объёму конструкция, но вместе с тем S велико, d мало, значит, ёмкость велика.

Энергия электрического поля

Пусть мы имеем два заряженных тела на расстоянии друг от друга. Мы уже знаем, что потенциальная энергия их взаимодействия выглядит так:

W12 = 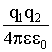. Эту формулу можно представить так:

W12 = q1 или так: W12 = q2 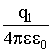. Эти формулы можно представить и так: W12 = q1 φ1 или так W12 = q2 φ2 , где φ1 – потенциал, создаваемый зарядом 2 в точке 1, а φ2 – потенциал, создаваемый зарядом 1 в точке 2. То есть q1 φ1 = q2 φ2 . Значит можно формально написать W12 = (q1 φ1 + q2 φ2 ) / 2 . Применим эту формулу для нахождения энергии конденсатора.

Обозначим U = φ1 – φ2 тогда получаем

W = (q+ φ1 + q -- φ2 ) / 2 = (q φ1 – q φ2 ) / 2 = q U / 2

Но ёмкость конденсатора равна C = q / U, значит W = C U2 / 2 .

С другой стороны ёмкость C = ε ε0 S / d, тогда получаем:

W = C U2 / 2 = 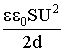= 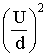S d = E2 V

Здесь мы обозначили буквой V = S d – объём, занимаемый полем Е .

Из этой формулы мы видим, что величину w = E2 можно определить, как плотность энергии электрического поля. Можно показать, что эта формула верна и для неоднородного поля, то есть для Е, зависящего от координат. В этом случае полная энергия, запасённая в поле W = ε E2 dV (интеграл по всему объёму, где находится поле).

Постоянный электрический ток

Электрическим током называется направленное движение электрических зарядов.

При этом возможны различные случаи:

1) Конвекционный ток.

Пусть мы имеем заряженное тело, которое движется в пространстве. Заряды тоже перемещаются вместе с телом, и значит, создаётся ток. Такой ток и называется конвекционным током.

2) Ток проводимости.

Пусть мы имеем проводник, в котором создано и поддерживается электрическое поле. Тогда положительные заряды начнут двигаться в одном направлении (по полю), а отрицательные – в противоположном направлении. Проводник может быть куском металла, тогда движутся электроны, а положительные ионы кристаллической решётки остаются на месте. Проводник может быть жидким (электролит), тогда движутся в разные стороны положительные и отрицательные ионы. Проводник может быть газообразным (например в лампах дневного света), тогда движутся электроны и положительные ионы. Во всех этих случаях ток называется током проводимости.

3) Ток в вакууме.

Пример – движение электронов в электронной лампе. Электроны испускаются раскалённым катодом лампы и под влиянием приложенного к лампе напряжения движутся к аноду.

Рассмотрим подробнее ток проводимости. Соединим заряженное тело (шар ) с землёй проводником, тогда по проводнику пойдут заряды, положительные и отрицательные, шар станет разряжаться и его заряд станет уменьшаться со временем. Величина скорости уменьшения заряда со временем, то есть и называется током в проводнике. Направлением тока условились считать направление движения положительных зарядов. Ясно, что в нашем примере через какое то время шар разрядится и ток прекратится. Что нужно, чтобы ток был постоянным? Нужно, чтобы заряд q не менялся со временем. То есть, нужен какой то источник возобновления заряда, нужны, как говорят, какие то сторонние силы, переносящие заряд на этот шар против электрического поля, которое он создаёт. Например, поставить какую то ионную пушку, которая выстреливала бы ионы, всё время подзаряжая наш шар. На вопросе о сторонних силах мы ещё остановимся.

А теперь что такое плотность тока, вернее вектор плотности тока. Этот вектор равен току через площадку, перпендикулярную к направлению движения зарядов, делённому на величину этой площадки.

Зная этот вектор в каждой точке проводника, можно найти силу тока через любую поверхность j = 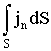. Если плотность тока постоянна по сечению проводника, то i = j S.

За единицу силы тока принимается ампер. При токе 1а через поперечное сечение проводника переносится заряд 1 кулон за каждую секунду.

Закон Ома

Пусть мы имеем проводник, между концами которого приложено напряжение U = φ1 – φ2 , то есть падение потенциала.

Г. Ом

В 1826 году Ом установил опытную зависимость тока от величины U, а именно: I = , где R называется электрическим сопротивлением. Итак, закон Ома: Ток, идущий в проводнике, равен отношению приложенного напряжения к сопротивлению проводника.

Единицей измерения сопротивления является 1 ом, то есть если I = 1 ампер, а U = 1 вольт, то R = 1 ом.

Сопротивление проводника зависит от его геометрических размеров и материала проводника. Для цилиндрических проводников эта зависимость выражается формулой R = ρ , где – длина проводника, S – его поперечное сечение, ρ – так называемое удельное сопротивление проводника, зависящее от его материала.

Преобразуем закон Ома, используя величины j и ρ.

I = = отсюда или j =

Часто применяют величину σ = , которая называется проводимостью, или удельной электропроводностью. Тогда получим:

Эта формула называется законом Ома в дифференциальной форме.

Закон Джоуля – Ленца

Известно, что при прохождении по проводнику тока проводник нагревается. Джоуль и Ленц обнаружили экспериментально, что при этом выполняется следующее соотношение:

Q = I2 R t, где Q – количество тепла, выделяющееся в проводнике, t – время протекания тока. Если ток меняется со временем, то можно написать более общую, очевидную формулу Q = I2 R dt.

Закон Джоуля – Ленца можно получить и расчётным путём. Пусть мы имеем проводник, к которому приложено напряжение U. За время dt через каждое сечение проходит заряд dQ = I dt. При этом электрическое поле совершает работу dA = U dq, или dA = U I dt = I2 R dt. Интегрируя, получаем: A = I2 R dt. Но эта работа вся превращается в тепло, отсюда и получаем закон Джоуля – Ленца. Таким образом, нагревание проводника происходит за счёт работы сил электрического поля при перемещении зарядов по проводнику.

Запишем теперь очевидную формулу

dQ = RdV I2 dt = ρ (j dS)2 dt = ρ j2 dV dt, где RdV – сопротивление элементарного объёма проводника dV = dS dℓ .

Величина w = является удельной мощностью, то есть количеством тепла, выделяющимся в единице объёма в единицу времени. Тогда мы имеем: w = ρ j2 . Но мы уже знаем, что j = E σ и ρ = 1 / σ . Отсюда получим: w = σ E2 Эти две формулы выражают закон Джоуля – Ленца в дифференциальной форме. Если мы знаем величину в каждой точке проводника и знаем её зависимость от времени, то можем получить самое общее выражение для закона Джоуля – Ленца:

Q = w dV dt = dt ρ j2 dV

Закон Ома для замкнутой цепи

Рассмотрим теперь, что происходит с электрическим током, когда электрическая цепь замкнута.

Пусть мы имеем какую то электрическую батарею в качестве источника питания и замкнутый на неё проводник. Что происходит в проводнике – течёт ток от плюса к минусу. Почему? Потому что есть разность потенциалов и электрическое поле в этом проводнике. Ну а что происходит в самой батарее – в ней тоже должен протекать ток, но течёт он уже против поля (от минуса к плюсу). Это означает, в батарее существуют какие то силы, заставляющие заряды двигаться против электрического поля. Эти силы называют обычно сторонними силами Fстор. Формально можно представить, что этим силам соответствует напряжённость электрического поля Естор = Fстор / q+, где q+ – единичный положительный заряд. Значит, внутри батареи есть два поля – Естор и противоположное ему обычное поле Е, конечно же Естор > E, иначе бы ток не шёл. Тогда закон Ома принимает вид:

j = σ ( E + Естор )

Чтобы разобраться в этом вопросе разберём такой пример: пусть мы имеем два бака с водой в гравитационном поле земли, между ними – трубы.

Естественно вниз течёт вода под действием поля Земли. Для того, чтобы поток воды не прекратился, нужно непрерывно поднимать воду на верхний уровень, например, насосом, который будет, таким образом, тоже сторонней силой, заставляющей воду двигаться против сил тяжести вверх. Насос этот могут верблюды крутить, электромотор может стоять – не важно, всё равно это будет сторонняя сила.

Точно так же и в замкнутой цепи электротока. Если источник тока это батарея, то сторонние силы – это силы химической реакции. Если рассмотреть случай электрофонарика на велосипеде, то источник тока – динамомашинка, приводимая в движение вращением колеса, таким образом, сторонние силы это в конечном итоге сила ваших ног.

Рассмотрим теперь закон Ома с учётом сторонних сил.

I = обычное выражение

I = с учётом сторонних сил, здесь ε12 = Естор dℓ

Величина ε12 называется электродвижущей силой (измеряется она в вольтах), она равна работе сторонних сил, отнесённой к единице положительного заряда.

МАГНЕТИЗМ

Магнитное поле в вакууме

Свойство магнитов притягивать железные предметы были известны ещё с времён древних греков. То, что Земля создаёт магнитное поле и поэтому магнитная стрелка компаса чувствует это поле, было известно также с древнейших времён. Сейчас мы можем сказать, что в пространстве, окружающем намагниченные тела, создаётся магнитное поле, которое и воздействует на другие намагниченные тела.

Итак, в электростатике взаимодействуют заряды тел, в магнитостатике взаимодействуют намагниченные тела. Однако существует принципиальная разница между электричеством и магнетизмом. А именно – существуют элементарные электрические заряды, а вот элементарных магнитных зарядов не существует.

Разъясним этот момент. В электростатике электрический диполь всегда можно разделить пополам, разрезать, и при этом образуются два тела, с положительным и отрицательным зарядом. Вспомним опыт с наведёнными электрическими зарядами.

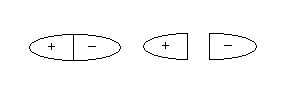
А вот в магнитостатике, если мы разрежем магнит, или магнитную стрелку пополам, всё равно образуются два новых магнита.

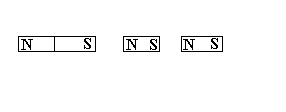
Можно сколько угодно раз и дальше их разрезать и все равно будут два полюса N и S, то есть магнитный диполь всегда остаётся диполем. Это и означает, что магнитных зарядов не существует.

Намагниченные тела или магнитные диполи при помещении их в магнитное поле испытывают со стороны поля момент сил, под действием которого магнитный диполь стремится развернуться вдоль поля. Многочисленные опыты, проведенные учёными – физиками в 19 и начале 20 века, привели их к выводу, что свойства магнитов обусловлены круговыми токами, текущими внутри этих магнитов.

Эти круговые, так называемые молекулярные электрические токи и порождают магнитное поле магнитов. Кроме того, было выяснено, что и электрический ток, текущий по проводникам, создаёт вокруг себя магнитное поле. Проводники с током взаимодействуют друг с другом посредством этих магнитных полей.

Взаимодействие токов

Пусть мы имеем два параллельных проводника с токами I1 и I2.

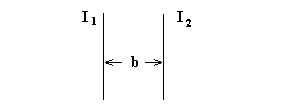
А. Ампер

Тогда из опыта следует, что если токи текут в одном направлении, то проводники притягивают друг друга, а если в противоположных друг другу направлениях – то отталкивают. Сила взаимодействия же определяется формулой f = , где μ0 – так называемая магнитная постоянная. Этот закон был установлен в 1820 году Ампером.

Магнитное поле

Если мы будем продолжать разрезание пополам намагниченного тела, магнитного диполя, как это мы уже делали, то, в конце концов, придём к элементарному круговому контуру с током, который всё равно будет обладать N и S полюсами, то есть будет магнитным диполем, и будет ориентироваться во внешнем магнитном поле вдоль его направления. Из опытов с моделями таких контуров следует, что вращательный момент, действующий на контур, пропорционален току и площади контура, причём неважно, какую форму имеет сам контур. Величину pm = I S называют магнитным моментом контура (в электростатике электрический момент диполя p = q ℓ). Замкнутый контур обладает ещё и направлением, поэтому: pm = I S n , где n – единичный вектор, направленный по нормали к плоскости контура по правилу правого винта (так условились).

В электростатике установлено, что на электрический диполь, помещённый в электрическое поле, действует вращательный момент, равный M = [ p E ] . Напишем аналогичную формулу для контура с током в магнитном поле: M = [ pm B ] . Входящий в эту формулу вектор B и определяет величину и направление магнитного поля. Называется он магнитной индукцией. Наряду с B величиной вводится величина H = = B / μ0 , которая называется напряжённостью магнитного поля. Мы видим, что логичнее было бы величину B называть напряжённостью магнитного поля. Однако исторически так сложилось, что B называют индукцией, а не напряжённостью.

Закон Био – Савара

Пусть мы имеем какой то провод, по которому течёт ток. Спрашивается, какое магнитное поле он создаёт в какой то точке пространства?

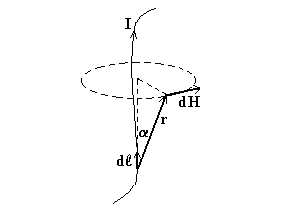
В 1820 году Био и Савар экспериментально изучили этот вопрос и выяснили, что от каждого элементарного кусочка проводника dℓ в точке r создаётся поле . А полная величина магнитного поля в точке r будет равна сумме всех полей d H от каждого элементарного участка провода. Для модуля d H получим:

d H =

Из закона Био – Савара следует, что единицей напряжённости магнитного поля является 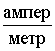= а / м.

Поле прямого тока

Согласно рисунку все dH от каждого элемента тока dℓ имеют одно и то же направление, поэтому сложим их модули. Кроме того, справедливо

d ℓ = da / Sin α = r dα / Sin α и r = b / Sin α

Тогда получим:

d H = = I = I = Sin α dα

Следовательно, сумма всех d H будет:

H =d H = Sin α dα = ( – Cos α) =

= ( – 1)( –1 – 1) =

Из выше сказанного следует, что линии напряжённости магнитного роля прямого тока это система концентрических окружностей, охватывающих проводник с током.

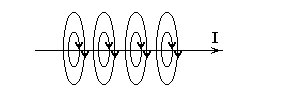
Величина магнитной индукции для этого случая

B = μ0H = μ0

Циркуляция вектора Н

Из электростатики мы знаем, что циркуляция вектора напряжённости электрического поля по любому замкнутому пути равна нулю, то есть El dl = 0 . Это связано с тем, электрическое поле является потенциальным полем.

Посмотрим теперь, как ведёт себя циркуляция вектора напряжённости магнитного поля, то есть Нl dl. Пусть мы имеем круговой замкнутый контур, охватывающий проводник с током.

Пусть ток перпендикулярен плоскости чертежа. Как мы знаем, линии напряжённости идут по концентрическим окружностям. Вычислим Нℓ dℓ по выбранному контуру. Тогда легко получаем, что

Нℓ dℓ = dℓ = I. Для произвольного контура ход вычислений следующий. Преобразуем Нℓ dℓ = Н dℓН . (dℓН – проекция вектора dℓ на направление вектора Н . Но dℓН = R dα , тогда

Нℓ dℓ = H R dα = R dα = dα . Значит

Нℓ dℓ = = I . То есть тот же результат.

Итак, циркуляция вектора напряжённости магнитного поля равна току, охватываемому этим контуром. Или более общий вид теоремы о циркуляции: Нℓ dℓ = Σ I.

Таким образом, мы видим, что циркуляция вектора Н будет равна нулю только для контуров, которые не охватывают токов. Отсюда следует, что магнитное поле не является потенциальным полем, для него не существует понятие потенциала. Поля такого типа называются вихревыми. То есть магнитное поле – вихревое. Линии напряжённости магнитного поля всегда замкнуты сами на себя, это как раз и связано с тем, что в природе не существует магнитных зарядов.

Напомним, что для электрического поля, которое является потенциальным, линии начинаются на + и оканчиваются на – зарядах, они не замкнуты сами на себя, то есть электрическое поле не является вихревым.

Теорема о циркуляции вектора Н позволяет сравнительно легко рассчитывать значения магнитных полей. Рассчитаем для примера магнитное поле соленоида. Возьмём бесконечно длинный соленоид.

Выберем согласно рисунку контур , точки 1, 2 – внутри соленоида, точки 3, 4 – снаружи. Из соображений симметрии ясно, что Н будет везде параллельно оси соленоида. Найдём циркуляцию Н по контуру

Нℓ dℓ = Нℓ dℓ +Нℓ dℓ +Нℓ dℓ +Нℓ dℓ

Интегралы 2-3 и 4-1 равны нулю, так как на этих участках Н перпендикулярно dℓ . Удалим прямую 3-4 на бесконечно большое расстояние, тогда и интеграл 3-4 будет равен нулю. В итоге получаем:

Нℓ dℓ = Нℓ dℓ = Н1-2 ℓ

Какой суммарный ток внутри нашего контура?

Ответ: Σ I = N I = nℓ I, где n – число витков на единицу длины. С другой стороны Нℓ dℓ = Σ I по теореме о циркуляции. Значит Н1-2 ℓ = nℓ I, отсюда получаем: Н1-2 = n I.

Полученный результат не зависит от того, на каком расстоянии от оси мы взяли отрезок 1 – 2 . Значит, поле внутри соленоида однородно, то есть постоянно по величине и направлению во всех точках.

Теперь – если отрезок 1 – 2 взять вне соленоида, то Σ I = 0 внутри нашего контура, значит вне соленоида Н = 0. Таким образом, в бесконечно длинном соленоиде магнитное поле полностью заключено внутри него. Линии Н идут внутри, параллельно оси соленоида. Если же соленоид конечной длины, то линии Н на торцах выходят из него и замыкаются сами на себя вне соленоида.

Магнитное поле в веществе

Магнитные свойства вещества

Всякое вещество способно намагничиваться, то есть способно под влиянием внешнего магнитного поля приобретать магнитный момент. Таким образом, все вещества являются магнетиками. Ампер предположил, что магнитные свойства веществ объясняются круговыми токами, текущими в каждой молекуле. Таким образом, каждая молекула или обладает собственным магнитным моментом, или может приобрести наведённый магнитный момент под действием внешнего магнитного поля. В отсутствие внешнего поля такие круговые молекулярные токи направлены беспорядочным образом, так что результирующий магнитный момент равен нулю. Если же наложить на магнетик внешнее поле, то магнитные моменты молекул ориентируются вдоль поля и таким образом магнетик намагничивается, то есть создаёт дополнительное магнитное поле B′, которое складывается с внешним полем B0. Тогда результирующее поле: В = B0 + B′ .

Намагничение вещества описывают вектором намагничения, то есть магнитным моментом единицы объёма вещества: J = 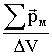, рм – магнитный момент отдельной молекулы.

Из опытов следует, что вектор намагничения прямо пропорционален вектору напряжённости магнитного поля в той же точке. То есть J = χ Н , χ – так называемая магнитная восприимчивость вещества.

До сих пор наши рассуждения были похожи на рассуждения о векторе поляризации в диэлектриках, там получается похожее соотношение P = κ ε0 E , κ – диэлектрическая восприимчивость. А вот дальше возникают различия. Дело в том, что в электростатике κ всегда положительная величина, а вот в магнитостатике χ может быть как больше нуля, так и меньше нуля. Соответственно все магнетики делятся на три группы:

1) Диамагнетики – χ отрицательно и невелико по величине

2) Парамагнетики – χ положительно и также невелико по величине

3) Ферромагнетики – χ положительно и достигает очень больших значений, в 109 – 1010 раз больше, чем у парамагнетиков.

Описание поля в магнетиках

Мы помним, что в электростатике реальное поле, действующее на заряды, это вектор напряжённости электрического поля Е, кроме того, вводится вспомогательный вектор D = ε ε0 E (вектор электрического смещения), удобство его в том, что облегчаются некоторые расчёты.

В магнитостатике же реальное поле, действующее на токи, это вектор магнитной индукции В. Кроме того вводится вспомогательный вектор, который называется напряжённостью магнитного поля Н, мы знаем, что для вакуума он равен Н = В / μ0 . Этот вектор также удобен тем, что облегчаются некоторые расчёты.

В случае магнитных полей в магнетике напряжённостью поля называется величина Н = – J , где J – вектор намагничения. Так как J = χ Н , получим Н (1+ χ) = . Обозначим (1+ χ) = μ , μ называется магнитной проницаемостью вещества. Итак, мы получаем:

Н =

Рассмотрим теперь подробнее формулу В = B0 + B′ . Итак мы имеем внешнее магнитное поле в вакууме с индукцией B0 . Поместим в это поле бесконечно длинный цилиндр из магнетика.

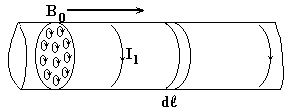
Тогда под влиянием поля все магнитные моменты, то есть элементарные круговые токи, повернутся так, что их плоскости станут перпендикулярны оси цилиндра. В каждой точке внутри цилиндра эти токи текут навстречу друг другу и взаимно компенсируются. Но на поверхности такого не происходит, и остаётся какой то нескомпенсированный ток. Пусть на единицу длины приходится ток I1. Тогда он создаст внутри цилиндра собственное поле H′ = I1 , точно так же как внутри соленоида создаётся поле с напряжённостью H′ = n I. В нашем случае n I, то есть ток на единицу длины соленоида это и есть I1

Отсюда следует, что собственная индукция такого поверхностного тока равна B′ = μ0 H′ = μ0 I1 . Итак вне стержня B′ = 0 , то есть В = B0 , а внутри В = B0 + B′ . Определим теперь величину I1 через вектор намагничения J = 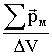. Возьмём в качестве ∆V объём диска длиной dℓ , тогда ∆V = S dℓ, и суммарный магнитный момент этого объёма pм = I dℓ S. Ток на длине dℓ равен I dℓ = I1 dℓ . Значит J = = I1 . Итак, вектор намагничения совпадает по величине с линейной плотностью тока. В результате получим: B′ = μ0 I1 = μ0 J, соответственно B′ = μ0 J . Таким образом В = B0 + μ0 J .

Мы знаем, что Н = – J , значит μ0 J = В – μ0 Н и В = B0 + В – μ0 Н и окончательно: Н = = Н0 .

То есть, Н (внутри магнетика) совпадает с Н0 (вне магнетика). Но этот вектор, как мы говорили, вспомогательный. Реальное же действующее поле это индукция, а она равна

В = μ0 μ Н = μ0 μ = μ B0 . Итак, внутри магнетика индукция усиливается в μ раз для парамагнетиков и ферромагнетиков и ослабляется в μ раз для диамагнетиков.

Закон Ампера

Как мы с вами уже знаем, согласно Амперу параллельно текущие токи притягиваются, а противоположно направленные – отталкиваются. Ампер установил и более общий закон, согласно которому на каждый элемент тока dℓ, помещенного в магнитное поле, действует сила df = I[dℓ B]. Модуль этой силы df = I B dℓ Sin α.

Применим этот закон для вычисления силы взаимодействия между параллельными проводами.

Расстояние между проводами b, тогда в месте расположения тока I 2 током I1 создаётся поле H1 = . B1 = μ0 H1 = . Значит, на единицу длины тока I2 действует сила

f21 = I2 B1 = . Таким образом, мы получили уже известную нам формулу.

Работа при перемещении тока в магнитном поле

Пусть мы имеем такую электрическую схему – два жёстких провода с током, по которым может скользить ещё один кусок провода.

Внешнее магнитное поле В направлено перпендикулярно плоскости чертежа. Сила Ампера f = I Bℓ направлена вправо, туда и начнёт скользить подвижный провод. При прохождении им пути ds работа силы будет равна dA = f ds = I Bℓ ds. Но произведение Bℓ ds является потоком вектора индукции В через заштрихованную площадку. Таким образом, dA = I dΦ .

Итак, работа, совершаемая при перемещении проводника в магнитном поле, равна произведению тока на магнитный поток, пересечённый движущимся проводником.

Можно показать, что полученная формула справедлива при любом движении любого проводника в произвольном магнитном поле. Кроме того, формула справедлива и для замкнутого движущегося контура с током.

Электромагнитная индукция

Мы уже знаем, что магнитное является следствием токов, текущих по проводникам, или круговых молекулярных токов в веществе. Возникает вопрос, нельзя ли возбудить ток в проводнике при помощи внешнего магнитного поля? Такая задача возникла в начале 19 века, и после многочисленных опытов Фарадею в 1831 году удалось добиться результата. Как сейчас говорят, Фарадей открыл явление электромагнитной индукции. Суть этого явления легко понять из опытов самого Фарадея.

М. Фарадей

Пусть мы имеем соленоид, к концам которого подключён чувствительный амперметр (гальванометр). Если постоянный магнит двигать или поворачивать по отношению к соленоиду, то при этом в соленоиде возникает слабый электрический ток. Если постоянный магнит заменить электромагнитом, то есть другим соленоидом, по которому течёт ток, то картина получается аналогичной. Кроме того, ток в гальванометре возникает также, если включать или выключать ток в электромагните.

Э. Ленц

Теперь что касается направления возникающих токов в таких опытах. В 1833 году Ленц установил правило для определения направления этих токов.

Это правило гласит: индукционный ток всегда направлен так, чтобы противодействовать причине, его вызывающей.

Например, если мы приближаем постоянный магнит к нашему соленоиду в первом опыте, то в соленоиде возникнет ток, вызывающий в соленоиде магнитное поле такого направления, что соленоид будет отталкивать от себя постоянный магнит.

Электродвижущая сила индукции

Если возникает индукционный ток, значит должна быть ЭДС, его вызывающая, то есть должна существовать ЭДС индукции. Найдём величину этой ЭДС. Возьмём контур с подвижным проводником.

Пусть внешнее магнитное поле направлено перпендикулярно чертежу. Мы знаем, что под действием силы Ампера проводник движется вправо и при этом совершается работа dA = I dΦ, где dΦ – изменение потока магнитного поля через заштрихованную площадку. Кроме того, мы знаем, что существует выделение тепла в сопротивлении проводников контура согласно закону Джоуля – Ленца dQ = I2 R dt. Следовательно, мы можем написать:

I ε dt = dQ + dA = I2 R dt + I dΦ , где I ε – мощность батареи контура. Из этого уравнения найдём : I = 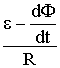, или можно написать I = , где εi – ЭДС индукции, которую мы и ищем. Следовательно, εi = – dΦ / dt.

Таким образом, ЭДС индукции в контуре равна скорости уменьшения потока вектора индукции, пронизывающего этот контур. Знак минус учитывает математически правило Ленца, о котором мы говорили. Найденная формула является универсальной и совершенно не зависит от способа изменения магнитного потока.

Явление самоиндукции

До сих пор мы рассматривали электромагнитную индукцию, разделяя контур, который создаёт магнитное поле, и контур, в котором возбуждаются индукционные токи. Оказывается, что явление электромагнитной индукции действует и в каждом отдельном контуре с током, если этот ток меняется со временем.

Пусть мы имеем любой контур, в котором течёт ток i. Этот ток создаёт вокруг себя магнитное поле и, значит, создаёт магнитный поток, пронизывающий сам контур. По закону Био – Савара создаваемое током поле пропорционально силе тока. Поэтому мы можем написать: Φ = L i, где L – какой то коэффициент пропорциональности. Вот этот коэффициент и называется индуктивностью нашего контура. L зависит от геометрии контура. Значит, мы можем получить значение ЭДС самоиндукции: εs = – dΦs / dt = – d(L i) / dt = – L di / dt.

В заключение вычислим индуктивность длинного соленоида. Пусть соленоид содержит N витков, по которым протекает ток i. Напряжённость магнитного поля внутри соленоида мы вычисляли, она равна H = n i, где n = N/ℓ ( ℓ – длина соленоида). Индукция же B = μ0 μ H = μ0 μ n i, где μ – относительная магнитная проницаемость среды внутри соленоида. Поток магнитного поля через каждый виток соленоида Φ = B S, все витки соединены последовательно, значит полный поток через все витков будет

ΦN = N Φ = N B S = n ℓ B S = μ0 μ n2 ℓ S i.

Но мы знаем, что должно быть ΦN = L i. Сравнивая эти две формулы, получим: L = μ0 μ n2 ℓ S = μ0 μ n2 V, где V – полный объём соленоида.

Сила Лоренца

Электрический ток это движение электронов вдоль проводника, с какой то скоростью u под действием приложенного электрического поля. Сила Ампера, действующая на проводник в магнитном поле, по сути, является суммой всех сил, действующих со стороны магнитного поля на отдельные движущиеся заряды. Найдём величину такой силы, действующей на отдельный заряд. Как мы знаем, согласно закону Ампера на элемент проводника с током I длиной ∆ℓ действует сила ∆f = I [∆ℓ B] . Сила тока I = j S, где j – плотность тока, S – сечение провода. Тогда I ∆ℓ = S ∆ℓ j , отсюда ∆f = S ∆ℓ [j B] .

Найдём величину j. Выделим элементарный объём dV = ds dℓ

Внутри этого объёма находится заряд q = e n ds dℓ , все электроны движутся с направленной скоростью u вдоль dℓ и за время dt = dℓ/u все уходят из объёма dV. Тогда ток i = q/dt = e n u ds, отсюда плотность тока j = e n u, или в векторной форме j = e n u .

Используя эту формулу, получим: ∆f = S ∆ℓ [j B] = S ∆ℓ e n [u B] . Учтём, что S ∆ℓ – объём провода длиной ∆ℓ , а S ∆ℓ n = N – полное число зарядов в этом объёме. Тогда получим

∆f = N e [u B] .

Отсюда следует, что на каждый отдельный заряд действует сила:

f = e [u B]

Вот это и есть сила Лоренца, которую мы искали, её модуль f = e u B Sin α , α – угол между u и B.

В заключение напишем общее выражение для силы, действующей на заряд, находящийся одновременно и в электрическом и в магнитном поле. f = e E + e [u B]

Движение заряженной частицы в магнитном поле

Рассмотрим несколько конкретных примеров.

1) Частица летит по направлению поля.

В этом случае f = e u B Sin α = 0 То есть частица летит вдоль линии индукции, не изменяя направления и скорости.

1) Поле направлено перпендикулярно плоскости, в которой лежит вектор скорости частицы. В этом случае сила Лоренца действует перпендикулярно направлению движения частицы, таким образом, изменяется направление движения, а абсолютная величина скорости не меняется.

Х. Лоренц

Это означает, что существует только нормальная составляющая ускорения равная wn = f / m = e u B / m. Движение частицы представляет собой движение по окружности, радиус которой определим из равенства wn = u2 / R = e u B / m. Это мы знаем из раздела Механика. Значит R = . Найдём период обращения частицы по этой орбите. T = 2 π R / u = . Таким образом, период не зависит от скорости частицы. Этот результат важен для понимания того, как происходит ускорение частиц в циклотроне.

Наконец третий пример. Частица влетает в магнитное поле под каким то углом по направлению поля. Разложим вектор скорости на две составляющие – параллельную и перпендикулярную к полю. Тогда параллельная составляющая не будет изменяться по величине и направлению, а перпендикулярная составляющая приведёт к вращению по окружности вокруг направления поля. В результате траектория движения является спиралью, ось которой совпадает с направлением поля. Таким образом, заряженные частицы, влетающие в магнитное поле, начинают навиваться на линии вектора В.

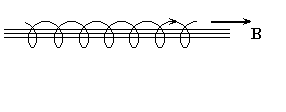
Движение частиц в магнитном поле Земли

Магнитное поле Земли можно приближённо представить, как поле магнитного диполя. Магнитное поле Земли отклоняется от поля диполя в местах магнитных аномалий – областей, где залегают железные руды (курская аномалия). Кроме того, поле Земли подвергается влиянию солнечного ветра. Как известно современной науке, на Землю из космического пространства непрерывно приходят потоки заряженных частиц, так называемые космические лучи. Кроме того, на Землю падает поток заряженных частиц, испускаемых Солнцем – солнечный ветер.

Что происходит с этими частицами, мы с вами теперь можем объяснить. Если частица подлетает к Земле в экваториальных областях, то она влетает поперёк магнитного поля Земли и под действием лоренцовой силы поворачивает по какой то дуге и улетает обратно. А вот вблизи полюсов падающие заряженные частицы начинают двигаться по спирали, навиваясь на линии вектора напряжённости магнитного поля Земли, и в результате падают на Землю. При этом, проходя верхние слои атмосферы, они вызывают свечение газов, которое люди давно уже наблюдали. Мы говорим о полярных сияниях, которые, как известно, наблюдаются только в крайних северных и в крайних южных областях Земли.

При так называемых вспышках на солнце, поток частиц с Солнца – солнечный ветер резко усиливается, что может вызвать изменения напряжённости магнитного поля Земли – магнитные бури.

На следующем рисунке представлено влияние потока частиц от Солнца на магнитное поле Земли.

Электромагнитное поле

Ток смещения

Понятие электрического тока смещения было впервые введено Максвеллом. До сих пор мы знали, что существует электрический ток проводимости, связанный с направленным движением зарядов. Рассмотрим теперь, что такое ток смещения Максвелла.

Пусть мы имеем плоский конденсатор, пластины которого заряжены зарядами +q и –q. Значит, на каждой пластине существует поверхностная плотность зарядов σ = q / S, а в пространстве между пластинами существует электрическое поле E = . Более удобен, как мы говорили, вектор электрической индукции D = ε ε0 E.

Следовательно, D = σ. Соединим пластины конденсатора проводником, тогда по нему пойдёт электрический ток, с пластин начнут стекать заряды. Величина этого тока i = dq/dt.

У внутренней границы пластины линии тока нормальны к поверхности пластины и плотность тока равна

j = i /S = dq /dt = (q /S) = dσ /dt.

Следовательно, можем написать j = d D /dt. В левой части этой формулы стоит плотность тока проводимости в металле, а в правой части скорость изменения вектора электрической индукции, или вектора электрического смещения. D меняется со временем, так как электрическое поле между пластинами в нашей задаче убывает. Значит формально можно считать, что величина d D /dt как бы продолжает линии тока через зазор между пластинами и замыкается с линиями тока проводимости на другой пластине конденсатора. По предложению Максвелла эту величину принято называть плотностью тока смещения.

Итак jсм = d D /dt.

Максвелл предположил далее, что это не только формальное понятие, и что ток смещения, так же как и настоящий ток проводимости должен, например, создавать в пространстве магнитное поле согласно закону Био-Савара. Впоследствии были поставлены специальные опыты, которые показали, что это действительно так, то есть ток смещения, или изменение напряжённости электрического поля создаёт в окружающем пространстве магнитное поле.

Пусть мы имеем пространство, в котором существует электрическое поле с вектором электрической индукции D, пусть это поле меняется со временем, тогда полный ток смещения, протекающий через какую то площадь S:

Д. Максвелл

iсм = jсм dS = dS = Dn dS

где Dn dS – поток вектора через площадь S, Dn – нормальная составляющая вектора D.

Вспомним теперь теорему о циркуляции вектора напряжённости магнитного поля по замкнутому контуру, охватывающему некоторую поверхность: Hℓ dℓ = Σ i, здесь Hℓ – проекция вектора H на направление перемещения вдоль контура, Σ i – сумма токов, пронизывающих контур. Тогда для тока смещения получим:

Hℓ dℓ = Dn dS

Итак, изменение со временем электрического поля в пространстве вызывает появление магнитного поля. Полученная нами формула описывает математически эту связь.

Вихревое электрическое поле.

Электромагнитное поле.

Вспомним закон электромагнитной индукции. Пусть мы имеем контур, который пронизывает магнитное поле. Если магнитное поле начнёт изменяться, то согласно этому закону в контуре возникнет ЭДС индукции, равная по величине εi = – dΦ/dt = – Bn dS, где

Φ = Bn dS – поток вектора магнитной индукции через поверхность, охватываемую контуром. ЭДС индукции в замкнутом контуре мы можем представить формулой εi = Eℓ dℓ . Справа в формуле циркуляция напряжённости электрического поля. Определённая такой формулой величина Eℓ = Евихр называется вихревым электрическим полем. Впервые его ввёл также Максвелл. Отметим, что для обычного электрического поля, создаваемого зарядами, циркуляция равна нулю, то есть поле является потенциальным. А вот для вихревого поля, создаваемого изменением магнитного поля во времени, циркуляция не равна нулю, то есть поле не является потенциальным.

Итак, запишем окончательно:

Eℓ dℓ = – (∂B /∂t)n dS

Причём слева мы уже под Е можем понимать полное поле Е = Епот + Евихр, результат не изменится, так как для Епот справедливо соотношение Eℓ dℓ = 0 .

Итак, окончательно мы имеем, что изменяющееся со временем магнитное поле создаёт в пространстве электрическое поле.

Вспоминая предыдущий раздел, можем сказать снова всё вместе:

1) переменное электрическое поле порождает магнитное поле.

2) переменное магнитное поле порождает электрическое поле.

Можно пойти и дальше, и сказать, что в силу этого в пространстве могут существовать, взаимно порождаясь, переменные электромагнитные поля. Причём это существование не зависит от того, есть ли в пространстве заряды и токи или их нет, есть ли в пространстве проводники и диэлектрики или их нет.

Таким образом, мы пришли к понятию свободных электромагнитных полей в вакууме или в среде. Такие свободные поля в виде электромагнитных волн распространяются в вакууме со скоростью, равной скорости света. Такие волны мы рассмотрим несколько позже.

Уравнения Максвелла

Открытие тока смещения позволило Максвеллу создать единую теорию электрических и магнитных явлений. Эта теория объяснила все известные опытные данные по электричеству и магнетизму и предсказала ряд новых явлений, которые впоследствии были подтверждены опытным путём. Основным из этих новых явлений было существование электромагнитных волн, распространяющихся со скоростью света. Оказалось, что и сам свет является электромагнитными волнами, только более высокой частоты.

Основу теории Максвелла составляют следующие четыре уравнения. Обо всех этих уравнениях мы уже говорили по отдельности, теперь напишем их вместе:

1-я пара уравнений Максвелла.

Eℓ dℓ = – (∂B /∂t)n dS

Bn dS = 0

Первое из этих уравнений мы только что рассматривали. Это, по сути, закон электромагнитной индукции. Второе означает уже известный нам факт, что линии индукции магнитного поля всегда замкнуты сами на себя, так как в природе не существует магнитных зарядов. Раз линии замкнуты, то конечно поток вектора через любую замкнутую поверхность равен нулю.

Теперь вторая пара уравнений:

Hℓ dℓ = jn dS + (∂D /∂t)n dS

Dn dS = ρ dV

Первое уравнение это теорема о циркуляции, учитывающая и токи проводимости, и токи смещения. Второе уравнение это теорема Гаусса, мы её уже знаем, то есть в природе существуют электрические заряды.

Написанные нами четыре уравнения являются уравнениями Максвелла в интегральной форме. Кроме того уравнения Максвелла можно записать в так называемой дифференциальной форме. Для этого нужно использовать две теоремы из раздела векторного исчисления курса высшей математики: теорему Стокса и теорему Гаусса- Остроградского, оперирующими понятиями ротора вектора и дивергенции вектора. Мы не будем приводить здесь этого вывода, приведём только окончательный результат:

Первая пара уравнений

rot E = – ∂B /∂t

div B = 0

Вторая пара уравнений

rot H = j + ∂D /∂t

div D = ρ

Кроме этого нужно помнить следующие формулы:

D = ε ε0 E B = μ μ0 H j = σ E

Уравнения Максвелла в дифференциальной форме очень часто используются для решения ряда практических задач. Например – нагрев токами высокой частоты металлических деталей (для закалки) или диэлектрических изделий (для сушки). Без уравнений Максвелла рассчитать такого рода промышленные установки просто невозможно. Применяются же такие установки во многих случаях.

Волновое уравнение

Можно показать, что из уравнений Максвелла можно получить математически электромагнитные волны, о которых мы уже говорили. Для этого нужно рассмотреть пространство без зарядов и токов, написать для этого случая уравнения Максвелла и воспользоваться некоторыми дополнительными формулами векторного исчисления. Приведём сразу окончательный результат – два уравнения, которые получаются после такой процедуры:

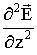+ + = ε0 μ0 ε μ

+ + = ε0 μ0 ε μ

Уравнение вида + + 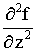= представляет собой волновое уравнение. Всякая функция, удовлетворяющая этому уравнению, описывает некоторую волну, движущуюся со скоростью v.

Таким образом, из вышеприведенного следует, что электромагнитные поля могут существовать в виде волн, фазовая скорость которых равна v = .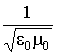

Для вакуума тогда получаем: v = 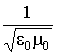= = 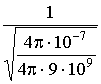3 108 м /сек. Таким образом, мы получили важный результат: в вакууме фазовая скорость электромагнитных волн совпадает со скоростью света, то есть

v = c

Плоская электромагнитная волна

Предположим, что электромагнитная волна распространяется вдоль координатной оси 0 – х. Тогда уравнения Максвелла, как можно показать, сведутся к двум уравнениям:

= ε0 μ0 ε μ = ε0 μ0 ε μ

При этом оказывается, что остальные составляющие E и H равны нулю, так что E = Ey и H = Hz. Кроме того, векторы E и H направлены по взаимно перпендикулярным осям y и z. Решения этих уравнений имеют вид: Ey = Em Cos (ωt – kx) Hz = Hm Cos (ωt – kx) . Общая картина плоской электромагнитной волны выглядит, как показано на рисунке.

Исследование и применение электромагнитных волн

Экспериментально электромагнитные волны впервые были наблюдены Герцем в 1888 году. Герц использовал для возбуждения волн высоковольтную искру между двумя электродами. В опытах Герца частота волны достигала до 108 герц, длина волны от 10 до 0,6 метра. Была доказана поперечность электромагнитных волн, показано, что их скорость близка к скорости света.

Изучение электромагнитных волн было с успехом продолжено в России, в 1884 году П. Лебедев получил волны длиной всего 6 мм. В 1886 году А. Попов впервые с помощью электромагнитных волн осуществил передачу текстового сообщения на расстояние 250 метров. Тем самым был осуществлён так называемый в то время беспроволочный телеграф, таким образом, было положено основание радиотехники. Современные схемы радиотехники, телевизионной техники, конечно, отличаются от простых схем Герца, Лебедева и Попова.

Г. Попов

Шкала электромагнитных волн

Такая шкала представлена на рисунке.

Видимый свет (C) – это электромагнитные волны, лежащие в диапазоне от λ = 780 нм (красный свет) до λ = 400 нм (фиолетовый свет). Однако видимый свет по своей физической природе ничем не отличается от других электромагнитных волн.

Радиоволны (A) охватывают диапазон от 106 м до 50 мкм. Область радиоволн смыкается с участком инфракрасных лучей (B). Граница между ними чисто условная и определяется способом их получения: радиоволны получают с помощью, например, ламповых генераторов, а инфракрасные лучи излучаются нагретыми телами.

С другой стороны к видимому участку спектра примыкают ультрафиолетовые лучи (D), которые можно, например, получить с помощью газового разряда.

К ультрафиолетовым лучам примыкают рентгеновские лучи (E) с длинами волн от 10 нм до 0,01 нм. За ними идёт область гамма-лучей (F). Рентгеновские лучи получают в специальных вакуумных высоковольтных трубках, гамма-лучи испускаются радиоактивными ядрами некоторых элементов.