Самосопряженные преобразования евклидовых пространств, свойства их собственных значений и собственных векторов

Определение 1. Линейное преобразование φ: E→E евклидова пространства E называется самосопряженным, если для любых x, y из E верно равенство (φ(x),y) = (x, φ(y)).

Свойства самосопряженных преобразований.

Пусть φ – самосопряженное преобразование евклидова пространства E. Тогда:

Утв.1. Если U – подпространство в E, инвариантное относительно φ (короче, φ - инвариантное подпространство) (т. е. ), то ортогональное дополнение также φ - инвариантно.

Доказательство. Для любых векторов , так как , следовательно, .

Замечание. Ограничение самосопряженного преобразования на инвариантное подпространство является самосопряженным, если на подпространстве рассматривать скалярное произведение, заданное во всем пространстве.

Утв.2. Собственные векторы , отвечающие различным собственным значениям, ортогональны.

Доказательство. Еcли φ(x1) = λ1x1, φ (x2) = λ2x2, x1 ≠ 0 ≠ x2, причем λ1≠ λ2, то □ .

Утв. 3. В ортонормированном базисе (о. н.б.) матрица A самосопряженного преобразования φ является симметрической: AT = A.

Доказательство. Если – ортонормированный базис в V, , – столбец координат вектора x, – строка его координат, то . Тогда

так что .

Так как для любых i, j от 1 до n (где – i-й столбец единичной матрицы), то , то есть AT = A. □

В доказательстве свойства собственных значений понадобится

Лемма. Любое линейного преобразование конечномерного действительного линейного пространства обладает одномерным или двумерным инвариантным подпространством U. (Одномерное порождено собственным вектором, а двумерное соответствует комплексному (не вещественному) характеристическому корню.)

Теорема 1. Все характеристические корни ( корни характеристического уравнения) самосопряженного преобразования (или симметрической матрицы) действительные.

Доказательство проводится индукцией по n=dim E.

Случай n =1 очевиден. При n = 2 в ортонормированном базисе

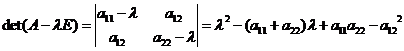= 0. Дискриминант этого уравнения , следовательно, .

При n > 2 сделаем индуктивное предположение о том, что у любой симметрической матрицы порядка <n все характеристические корни действительные. Допустим, что хотя бы один характеристический корень матрицы A мнимый. Согласно лемме, существует двумерное инвариантное подпространство U. По утверждению 1, также инвариантно.

В ортонормированном базисе, составленном из базисов подпространств U и , матрица преобразования имеет блочный вид , где A1 - симметрическая матрица 2 порядка, A2 – симметрическая матрица порядка n-2, . По предположению индукции, уравнение =0 имеет все действительные корни, следовательно

(с учетом случая 2), уравнение 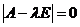– тоже –противоречие, следовательно, теорема 1 верна для всех n. □

Теорема2. Для любого самосопряженного преобразования существует ортонормированный базис из его собственных векторов. Матрица преобразования в этом базисе диагональна: 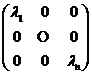, где - собственные значения матрицы этого преобразования.

Доказательство теоремы 2 – индукция по n.

При n = 1 доказывать нечего. При n > 1 пусть – какой-либо характеристический корень (действительный, по теореме 1), h1 соответствующий собственный вектор (можно сразу взять ) и – одномерное инвариантное подпространство. Согласно утв.1, инвариантно размерности n–1, и для ограничения преобразования на , по предположению индукции, существует ортонормированный базис 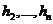из собственных векторов. Тогда – искомый базис.

□Пример. В некотором о. н.б. в R3 линейное преобразование φ задано матрицей . Найти для φ ортонормированный базис из собственных векторов и записать в нем матрицу преобразования.

□

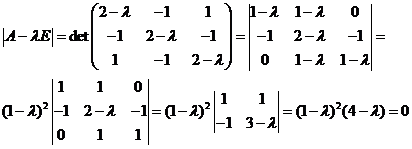
Собственные векторы: , 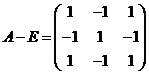. Система уравнений для собственных векторов: , так что имеются два линейно независимых собственных вектора. Можно взять 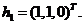Второй линейно независимый собственный вектор ищем ортогональный к h1, т. е. как решение системы 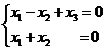. Например, , т. е.

Собственный вектор для , по утв. 2, ортогонален к , так что в трехмерном пространстве он единственный с точностью до множителя вектор из . Читая уравнение как скалярное произведение , без вычислений находим (Разумеется, можно было решить характеристическую систему уравнений для и получить то же самое.)

Окончательно, нормируя, получаем . В этом базисе .□

Можно упомянуть 2 типичных примера самосопряженных преобразований.

Пусть E – n-мерное евклидово пространство, U – подпространство в E, 0 ≠ U ≠ V, тогда любой вектор единственным образом представляется в виде .

Пример 1. Ортогональное проектирование V на U: . Проверка самосопряженности: . Ядром преобразования является U.

Собственные векторы: . В о. н.б., составленном из базисов подпространств U, , матрица преобразования равна , если .

Пример 2. Ортогональная симметрия (или зеркальное отражение) S пространства E относительно U: S(x) = y – z. Проверить самосопряженность можно аналогично.

Собственные векторы: . В о. н.б., составленном из базисов подпространств U, , матрица оператора равна .