1. , , . Экологический мониторинг. Учебник в 2-х том. Т.2. –СПб,1998.-53-60 с.
Погрешности измерений
Основные понятия
Истинное значение величины — значение величины, которое идеальным образом характеризовало бы в качественном и количественном отношении соответствующую величину.
Действительное значение величины — значение величины, полученное экспериментальным путем и настолько близкое к истинному значению, что в поставленной измерительной задаче может быть использовано вместо него.
Результат измерения — значение величины, полученное путем ее измерения.
Сходимость результатов измерений — близость друг к другу результатов измерений одной и той же величины, выполненных повторно одними и теми же средствами, одним и тем же методом в одинаковых условиях и с одинаковой тщательностью.
Воспроизводимость результатов измерений — близость друг к другу результатов измерений одной и той же величины, полученных в разных местах, разными методами, разными средствами, разными операторами, в разное время, но приведенных к одним и тем же условиям измерений (температуре, давлению, влажности и др.).
Погрешность результата измерения (погрешность измерения) — отклонение результата измерения от истинного (действительного) значения измеряемой величины.
Погрешность средства измерений — разность между показанием средства измерений и истинным (действительным) значением измеряемой величины.
Основная погрешность средства измерений — погрешность средства измерений, применяемого в нормальных условиях.
Дополнительная погрешность средства измерений — составляющая погрешности средства измерений, возникающая вследствие отклонения какой-либо из влияющих величин от ее нормального значения или вследствие ее выхода за пределы нормальной области значений.
Систематическая погрешность измерения — составляющая погрешности результата измерения, остающаяся постоянной или же закономерно изменяющаяся при повторных измерениях одной и той же величины.
Поправка — значение величины, вводимое в неисправленный результат измерения с целью исключения составляющих систематической погрешности.
Исправленный результат измерения — полученное при измерении значение величины, уточненное путем введения в него необходимых поправок на действие систематических погрешностей.
Неисключенная систематическая погрешность (НСП) измерения — составляющая погрешности результата измерения, обусловленная погрешностями вычисления и введения поправок или же систематической погрешностью, поправка на действие которой не введена.
Случайная погрешность измерения — составляющая погрешности результата измерения, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях одной и той же величины.
Абсолютная погрешность измерения — погрешность измерения, выраженная в единицах измеряемой величины.
Относительная погрешность измерения — погрешность измерения, выраженная отношением абсолютной погрешности к действительному или измеренному значению измеряемой величины.
Инструментальная погрешность измерения — составляющая погрешности измерения, обусловленная погрешностью применяемого средства измерений.
Погрешность метода измерений (методическая погрешность) — составляющая систематической погрешности измерений, обусловленная несовершенством метода измерений.
Погрешность из-за изменений условий измерения — составляющая систематической погрешности измерения, являющаяся следствием неучтенного влияния отклонения в одну сторону какого-либо из параметров, характеризующих условия измерений, от установленного значения.
Субъективная погрешность измерения — составляющая погрешности измерения, обусловленная индивидуальными особенностями оператора.
Статическая погрешность измерения — погрешность результата измерения, свойственная условиям статического измерения, т. е. измерения величины, принимаемой за неизменную на протяжении времени измерения.
Динамическая погрешность измерения — погрешность результата измерения, свойственная условиям динамического измерения, т. е. измерения изменяющейся по размеру величины.
Доверительные границы погрешности результата измерения — наибольшее и наименьшее значения погрешности измерения, ограничивающие интервал, внутри которого с заданной вероятностью находится значение погрешности результата измерения.
Точность результата измерения — характеристика качества измерения, отражающая близость к нулю погрешности результата измерения.
Точность средства измерений — характеристика качества средства измерений, отражающая близость его погрешности к нулю.
Вследствие погрешностей, присущих средству измерений, выбранному методу измерений, отклонению условий измерения от номинальных условий, а также из-за других причин результат практически каждого измерения отягощен погрешностью. Эта погрешность оценивается и приписывается полученному результату. Строго говоря, погрешность результата измерения (кратко — погрешность измерения) — это отклонение результата измерения от истинного значения измеряемой величины. Однако истинное значение величины, в гносеологическом смысле являющееся аналогом абсолютной истины, никогда не известно. Поэтому на практике вместо него используют действительное значение — значение величины, полученное экспериментальным путем и настолько близкое к истинному значению, что в поставленной измерительной задаче может быть использовано вместо него (например, значение, полученное путем измерений с очень высокой точностью). Тогда погрешность измерений определяется выражением
DС = Сизм-Сдейств,
где С изм — значение величины, полученное на основании измерений;
Сдейств — значение величины, принятое за действительное.
Погрешности измерений могут быть классифицированы по следующим признакам: по характеру проявления — систематические и случайные; по способу выражения — абсолютные и относительные; по условиям изменения измеряемой величины — статические и динамические; по источнику возникновения — инструментальные, погрешности метода, погрешности из-за изменений условий измерения и субъективные; по полноте охвата измерительной задачи — частные и полные (чаще их называют суммарными); по отношению к единице величины — погрешности воспроизведения единицы, хранения единицы и передачи размера единицы.
Систематические погрешности подлежат исключению, насколько это возможно, путем введения поправок или градуировкой прибора. Однако полностью их исключить практически невозможно. Поэтому введено понятие «неисключенная систематическая погрешность» (кратко — НСП). Это погрешность результата измерений, обусловленная погрешностями вычисления и введения поправок или же систематической погрешностью, поправка на действие которой не введена. Например, с целью исключения инструментальной систематической погрешности аналитического измерения, обусловленной нестабильностью функции преобразования прибора, периодически проводят градуировку прибора по эталонным мерам (поверочным газовым смесям или стандартным образцам). Однако, несмотря на это, в момент измерения все равно будет некоторое отклонение действительной функции преобразования от градуировочной зависимости, обусловленное погрешностью градуировки и нестабильностью прибора за время, прошедшее после градуировки. Поскольку значение этой погрешности остается неизвестным, она классифицируется как НСП.
НСП количественно оценивают границами в (без указания знака), значения которых обычно устанавливаются путем ориентировочного расчета (например, пределы допускаемых погрешностей, если случайные составляющие малы). Если имеется несколько причин возникновения НСП, то отдельно оценивают НСП, обусловленную каждой причиной, а затем их суммируют в соответствии со следующим правилом:

где N — число составляющих НСП; к — коэффициент зависимости суммы составляющих от выбранной доверительной вероятности Р при их равномерном распределении. При Р = 0,99 к=1,4, при Р = 0,95 к= l, l.
Случайная погрешность измерения — составляющая погрешности результата измерения, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях одной и той же величины.
Причины случайных погрешностей: погрешности округления при отсчете показаний, вариация показаний, случайные изменения условий измерений и др. Случайные погрешности вызывают рассеяние результатов измерений в серии. В основе теории погрешностей лежат два положения, подтверждаемые практикой:
— при большом числе измерений случайные погрешности одинакового числового значения, но разного знак, встречаются одинаково часто;
— большие (по абсолютному значению) погрешности встречаются реже, чем малые.
Отсюда следует важный для практики вывод: при увеличении числа измерений случайная погрешность результата, полученного из серии измерений, уменьшается, так как сумма погрешностей отдельных измерений данной серии стремится к нулю. Несмотря на это, обязательно проводится оценивание случайной погрешности результата измерений. Ее оценкой является среднее квадратическое отклонение (СКО) результата многократных измерений, вычисляемое по формуле
 (3.6)
(3.6)
где Сi — результат i-го измерения,
![]() (3.7)
(3.7)
`С — среднее арифметическое результатов измерений, принимаемое за результат серии измерений.
Если результат измерений исправлен введением поправок, СКО равно средней квадратической погрешности (СКП) результата измерений.
Методам оценивания погрешностей измерений посвящено большое количество монографий и учебных пособий. Учащимся можно рекомендовать монографию , и , отличающуюся доступностью изложения материала без ущерба для строгости и полноты. В этом разделе мы ограничимся только наиболее распространенными в аналитике прямыми многократными измерениями. Метод статистической обработки их результатов регламентирован ГОСТ 8.201-76. Он предусматривает следующие операции:
1. Исключение известных систематических погрешностей из результатов измерений.
2. Вычисление по формуле (3.7), в которой Сi — исправленный результат i-го измерения, результата многократных измерений `С.
3. Вычисление оценки СКО S(C) результата однократного измерения по формуле
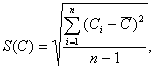
![]() (3.8)
(3.8)
4. Вычисление оценки СКО S(`C) результата многократного измерения по формуле (3.6) либо по формуле
![]() . (3.9)
. (3.9)
5. Проверка гипотезы о том, что результаты измерений принадлежат нормальному распределению. При числе измерений n>50 чаще всего используют критерий Пирсона. Мы его рассматривать не будем, так как такое количество измерений в серии на практике встречается очень редко. При n < 10 проверить гипотезу о виде закона распределения невозможно. При 10 < п <50 также трудно судить о виде распределения. Поэтому гипотезу о нормальности закона распределения рекомендуется проверять по составному (из двух критериев) критерию. Если эта гипотеза отвергается хотя бы по одному из критериев, считают, что распределение отлично от нормального.
Критерий 1. Вычисляют значение
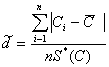 (3.10)
(3.10)
где ![]() — смещенное СКО. Гипотеза о нормальности подтверждается, если
— смещенное СКО. Гипотеза о нормальности подтверждается, если
![]() (3.11)
(3.11)
где d1-q1/2, dq1/2 - процентные точки распределения значений d при уровне значимости критерия q1, которые находят по таблице 3.2.
Таблица 3.2 Статистика d
|
n |
(q1 /2)*100% |
(1- q1 /2)100% | ||
|
1 % |
5% |
95% |
99% | |
|
11 |
0,94 |
0,91 |
0,72 |
0,67 |
|
16 |
0,91 |
0,89 |
0,72 |
0,68 |
|
21 |
0,90 |
0,88 |
0,73 |
0,69 |
|
26 |
0,89 |
0,87 |
0,74 |
0,70 |
|
31 |
0,88 |
0,86 |
0,74 |
0,71 |
|
36 |
0,88 |
0,86 |
0,74 |
0,72 |
|
41 |
0,87 |
0,85 |
0,75 |
0,72 |
|
46 |
0,87 |
0,85 |
0,75 |
0,72 |
|
51 |
0,86 |
0,85 |
0,75 |
0,73 |
Критерий 2. Гипотеза о нормальности распределения подтверждается, если не более m разностей (Ci -`C) превысили значения z05P S(C),где z05P —верхняя 100*0,5Р — процентная точка нормированной функции Лапласа. При числе измерений 10 < n < 20 принимают m=1, при 20 <n<50 принимают m=2. Доверительную вероятность P(n, q) определяют по n и уровню значимости критерия q2 как корень уравнения
![]()
Значения Р можно найти из таблицы 3.3, z0,5P — из таблицы 3.4.
Таблица 3.3 Значения Р для нахождения z0,5P
|
n |
m |
q2 *100% | ||
|
1 % |
2% |
5 % | ||
|
10 |
1 |
0,98 |
0,98 |
0,96 |
|
11-14 |
1 |
0,99 |
0,98 |
0,97 |
|
15-20 |
1 |
0,99 |
0,99 |
0,98 |
|
21-22 |
2 |
0,98 |
0,97 |
0,96 |
|
23 |
2 |
0,98 |
0,98 |
0,96 |
|
24-27 |
2 |
0,98 |
0,98 |
0,97 |
|
28-32 |
2 |
0,99 |
0,98 |
0,97 |
|
33-35 |
2 |
0,99 |
0,98 |
0,98 |
|
36-49 |
2 |
0,99 |
0,99 |
0,98 |
Таблица 3.4 Значения Р-процентных точек нормированной функции Лапласа
|
P*100% |
90 |
95 |
96 |
97 |
98 |
99 |
|
z0,5P |
1,65 |
1,96 |
2,06 |
2,17 |
2,33 |
2,58 |
Уровень значимости составного критерия определяется так:
q£q1 + q2.
Пример. Проверим гипотезу о нормальности распределения результатов измерений молярной доли СО в азоте в ГСО, представленных в таблице 3.5.
Найдем СКО S(C) и S*(C):
![]()
Оценка параметра ![]() составит:
составит: ![]()
Q1 = 2%. Из таблицы 3.2 находим: d1%=0,92, d99% =0,68. Так как 0,68<0,88<0,92, то критерий 1 выполняется.
q2 =5%. Из таблицы 3.3 для n=14 находим: Р=0,97. Из таблицы 3.4 определим: z0,5P =2,17. Тогда z05P S(C)=3,245*2,17 = 7,042 . Согласно критерию 2 не более одной разности | Сi – С ½ может превзойти 7,042. Таблица 3.5 показывает, что таких разностей нет. Следовательно, гипотеза о нормальности распределения подтверждается.
Уровень значимости составного критерия q £ 0,02 + 0,05 = 0,07. Таким образом, гипотеза о нормальности распределения результатов измерений подтверждается при уровне значимости не более 0,07.
Таблица 3.5 Результаты измерений молярной доли СО в азоте в баллоне — ГСО
|
Сi, ррм |
Сi -`С, ррм |
(Сi -`С)2 ррм2 |
Ci, ррм |
Сi -`С, ррм |
(Сi -`С)2 ррм2 |
|
45,00 |
4,301 |
18,498601 |
43,33 |
2,631 |
6,922161 |
|
36,25 |
-4,449 |
19,793601 |
40,63 |
-0,069 |
0,004761 |
|
42,50 |
1,801 |
3,243601 |
36,25 |
-4,449 |
19,793601 |
|
45,00 |
4,301 |
18,498601 |
42,50 |
1,801 |
3,243604 |
|
37,50 |
-3,199 |
10,233601 |
39,17 |
-1,529 |
2,337841 |
|
38,33 |
-2,369 |
5,612161 |
45,00 |
4,301 |
18,498601 |
|
37,50 |
-3,199 |
10,233601 |
40,83 |
0,131 |
0,017161 |
|
|
569,786 |
å½Сi -`С½=38,530 |
136,931497 | ||
6. Вычисление доверительных границ e (без учета знака) случайной погрешности измерения по формуле
![]() (3.13)
(3.13)
где t (n -1, Р) — коэффициент Стьюдента, который в зависимости от числа измерений n и доверительной вероятности Р находят из таблицы 3.6.
7. Вычисление границ q НСП результата измерения.
8. Вычисление доверительных границ D погрешности результата измерения.
Если q/S(`C)<O,8, то НСП пренебрегают и принимают: D= e.
|
Таблица 3.6 Значение коэффициента t для случайной величины, имеющей распределение Стьюдента с n-1 степенями свободы | |||||
|
n-1 |
Р = 0,95 |
Р = 0,99 |
n-1 |
Р = 0,95 |
Р = 0,99 |
|
3 |
3,182 |
5,841 |
16 |
2,120 |
2,921 |
|
4 |
2,776 |
4,604 |
18 |
2,101 |
2,878 |
|
5 |
2,571 |
4,032 |
20 |
2,086 |
2,845 |
|
6 |
2,447 |
3,707 |
22 |
2,074 |
2,819 |
|
7 |
2,365 |
3,499 |
24 |
2,064 |
2,797 |
|
8 |
2,306 |
3,355 |
26 |
2,056 |
2,779 |
|
9 |
2,262 |
3,250 |
28 |
2,048 |
2,763 |
|
10 |
2,228 |
3,169 |
30 |
2,043 |
2,750 |
|
12 |
2,179 |
3,055 |
¥ |
1,960 |
2,576 |
|
14 |
2,145 |
2,977 |
Если q/S(`C)>8, то пренебрегают случайной погрешностью и принимают: D=q.
Если эти неравенства не выполняются, D вычисляют по формуле
D= KSå, (3.14)
где 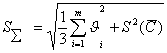 — оценка СКО суммарной погрешности измерения;
— оценка СКО суммарной погрешности измерения;
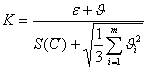
— коэффициент, зависящий от соотношения случайной погрешности и НСП.
9. Результат измерений записывают в следующей форме:
`С ± D, Р. Это означает, что измеряемая величина С с доверительной вероятностью Р находится внутри интервала: [`С - D, `С +.D ].
Понятие погрешности
- Погрешность вычислений ёмкости в программной среде Tor elcut
- Погрешности измерений
- Теория погрешностей Измерение физических величин
- Погрешность средств измерения
- Погрешности и условия применения импульсных методов определения теплофизических характеристик материалов
- Погрешности измерений физических величин
- Факторы, влияющие на погрешность изотопно-молекулярного анализа оксида азота
- Урок 2.2 Тема. Физические величины. Измерение физических величин. Точность и погрешность измерений
Проекты по теме:
 Основные порталы (построено редакторами)
Основные порталы (построено редакторами)





