УДК 534.1
, д. т.н., профессор;
РАСЧЕТ СОБСТВЕННЫХ ЧАСТОТ ИЗГИБНЫХ КОЛЕБАНИЙ ОГРАНОЧНОГО ДИСКА
В статье описана методика расчета собственных частот изгибных колебаний ограночного диска. Выполнено сравнение расчетных значений собственных частот с экспериментальными данными.
Ограночный диск представляет собой режущий инструмент с алмазоносным поверхностным слоем, применяемый для шлифования и полирования монокристаллов алмаза и других сверхтвердых материалов. Алмазоносный слой на рабочей поверхности ограночного диска традиционно формируется методом механического шаржирования (укатки). Однако данная технология формирования алмазоносного слоя не обеспечивает высоких эксплуатационных показателей инструмента. Как показали предшествующие исследования, эффективным методом повышения эксплуатационных показателей ограночных дисков является формирование алмазоносного слоя методом укатки с наложением ультразвуковых колебаний на деформирующий инструмент [1]. Однако, в рамках проведенных исследований недостаточное внимание было уделено анализу характера взаимодействия деформирующего инструмента с ограночным диском в условиях ультразвукового воздействия. Вместе с тем, подобный анализ должен быть проведен с целью выбора рациональных режимов ультразвукового воздействия. В частности, необходимо учитывать возможность совпадения частоты воздействия с одной из собственных частот изгибных колебаний диска. В связи с этим была поставлена задача разработки методики расчета этих частот, решение которой описано в данной статье.
Из работы [2] известно, что свободные изгибные колебания пластин описываются уравнением вида
![]() , (1)
, (1)
где ![]() – оператор Лапласа,
– оператор Лапласа,
![]() – колебательное смещение,
– колебательное смещение,
![]() – плотность материала пластины,
– плотность материала пластины,
![]() – коэффициент Пуассона,
– коэффициент Пуассона,
E – модуль упругости,
h – толщина пластины.
Величину ![]() называют цилиндрической жесткостью пластины.
называют цилиндрической жесткостью пластины.
В случае гармонических колебаний с круговой частотой ![]() функция колебательных смещений может быть представлена в виде
функция колебательных смещений может быть представлена в виде
![]() , (2)
, (2)
где ![]() – амплитуда колебательных смещений.
– амплитуда колебательных смещений.
С учетом выражения (2) уравнение (1) принимает вид
![]() , (3)
, (3)
где ![]() .
.
Параметр k естественно называть волновым числом по аналогии со случаем продольных колебаний стержней.
Надстрочный знак будет в дальнейшем для простоты опускаться.
Колебания круглой пластины (диска) удобно описывать с помощью функций, зависящих от цилиндрических координат. Оператор Лапласа в цилиндрических координатах определяется выражением
![]() .
.
Функция ![]() в силу своей периодичности по угловой координате может быть разложена в ряд Фурье. Так как поле колебательных смещений для диска обладает осевой симметрией, то функция амплитуд колебательных смещений является четной по угловой координате и ее ряд Фурье не содержит синусов, то есть имеет вид
в силу своей периодичности по угловой координате может быть разложена в ряд Фурье. Так как поле колебательных смещений для диска обладает осевой симметрией, то функция амплитуд колебательных смещений является четной по угловой координате и ее ряд Фурье не содержит синусов, то есть имеет вид
![]() . (4)
. (4)
Каждый из членов ряда (4) описывает распределение амплитуды колебательных смещений по поверхности диска для n-ой моды изгибных колебаний. Нулевая мода представляет собой радиальную изгибную волну, для которой амплитуды колебательных смещений не зависят от угловой координаты. Моды высших порядков представляют собой круговые изгибные волны.
Подставив ряд (4) в уравнение (3), получим для определения коэффициентов ряда уравнение
 . (5)
. (5)
Если опустить индекс n, то общее решение уравнения (5) запишется в виде
![]() . (6)
. (6)
Здесь ![]() и
и ![]() – функции Бесселя 1-го и 2-го рода n-го порядка,
– функции Бесселя 1-го и 2-го рода n-го порядка,
![]() и
и ![]() – модифицированные функции Бесселя 1-го и 2-го рода n-го порядка.
– модифицированные функции Бесселя 1-го и 2-го рода n-го порядка.
В случае сплошного диска должно выполняться условие  , так как в противном случае решение (6) неограниченно возрастает по мере приближения к центру диска. Поэтому для сплошного диска необходимо рассматривать только два граничных условия, представляющих собой условия закрепления внешнего контура диска.
, так как в противном случае решение (6) неограниченно возрастает по мере приближения к центру диска. Поэтому для сплошного диска необходимо рассматривать только два граничных условия, представляющих собой условия закрепления внешнего контура диска.
Ограночный диск в силу особенностей его конструкции может быть представлен как диск, жестко закрепленный по внутреннему контуру радиусом ![]() и имеющий свободный наружный контур радиусом
и имеющий свободный наружный контур радиусом ![]() , то есть не может быть рассмотрен как сплошной диск. В связи с этим для него необходимо рассмотреть 4 граничных условия: два на внешнем контуре и два – на внутреннем. Конструкция ограночного диска и размеры, используемые при расчете его собственных частот колебаний, изображены на рисунке 1.
, то есть не может быть рассмотрен как сплошной диск. В связи с этим для него необходимо рассмотреть 4 граничных условия: два на внешнем контуре и два – на внутреннем. Конструкция ограночного диска и размеры, используемые при расчете его собственных частот колебаний, изображены на рисунке 1.
Для формулировки граничных условий введем следующие величины:
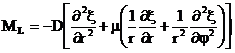 – изгибающий момент на контуре диска,
– изгибающий момент на контуре диска,
 – крутящий момент на контуре диска,
– крутящий момент на контуре диска,
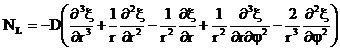 – поперечная сила на контуре диска.
– поперечная сила на контуре диска.

Рисунок 1 – схема конструкции ограночного диска
На свободном контуре (![]() ) должны выполняться условия
) должны выполняться условия
 (7)
(7)
На жестко закрепленном контуре (![]() ) граничные условия принимают вид
) граничные условия принимают вид
 (8)
(8)
Подставив в граничные условия (7) и (8) n-ый член ряда (4), получим систему из четырех однородных линейных уравнений для определения неизвестных постоянных, входящих в выражение (6). Эта система имеет нетривиальное решение при условии, что детерминант матрицы коэффициентов при неизвестных равен нулю, то есть
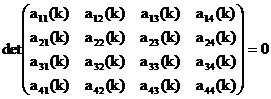 . (9)
. (9)
Функцию ![]() будем называть частотной функцией.
будем называть частотной функцией.
Условие (9) выполняется только для ряда дискретных значений волнового числа k, соответствующих собственным частотам колебаний диска. Элементы матрицы A(k) определяются выражениями
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Выражения для коэффициентов 2-го, 3-го и 4-го столбцов матрицы получаются из приведенных выражений заменой функций Бесселя 1-го рода на функции Бесселя 2-го рода и модифицированные функции Бесселя 1-го и 2-го рода.
Для упрощения расчетов воспользуемся рекуррентными формулами для вычисления производных функций Бесселя [3]:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
После исключения производных выражения для элементов матрицы A(k) с точностью до постоянных множителей принимают вид
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]()
![]() .
.
Выражения для коэффициентов ![]() получаются из выражений для коэффициентов
получаются из выражений для коэффициентов  путем замены функций Бесселя 1-го рода на функции Бесселя 2-го рода. Для получения выражений для коэффициентов
путем замены функций Бесселя 1-го рода на функции Бесселя 2-го рода. Для получения выражений для коэффициентов ![]() необходимо в выражениях для коэффициентов
необходимо в выражениях для коэффициентов  изменить знак на противоположный и заменить модифицированные функции Бесселя 1-го рода модифицированными функциями Бесселя 2-го рода.
изменить знак на противоположный и заменить модифицированные функции Бесселя 1-го рода модифицированными функциями Бесселя 2-го рода.
Расчет собственных частот был выполнен для мод 6-го и 11-го порядка, наблюдавшихся экспериментально. Корни частотной функции определялись из ее графика, при построении которого использовались значения, рассчитанные с помощью программы MathCAD 7.0 Professional. Графики частотной функции для мод 6-го и 11-го порядка приведены на рисунке 2.
При расчете частотных функций были использованы следующие значения:
· радиус внешнего контура диска  ;
;
· радиус внутреннего контура диска  ;
;
· коэффициент Пуассона материала диска (сталь) ![]() .
.
Наименьший положительный корень частотной функции соответствует собственной частоте, для которой форма собственных колебаний не содержит узловых окружностей. Второй положительный корень соответствует наличию одной узловой окружности. Обозначим число узловых окружностей как m. Расчетные значения собственных частот для различных значений m и n представлены в таблице 1.
| Волновое число k |
| Волновое число k |
Рисунок 2 – Графики частотной функции:
а) для моды 6-го порядка; б) для моды 11-го порядка
Таблица 1 – Расчетные собственные частоты колебаний диска, кГц
Число узловых окружностей | Порядок моды | |
n=6 | n=11 | |
m=0 | 5,36 | 16,70 |
m=1 | 14,82 | 34,92 |
При расчете были использованы следующие значения:
· толщина диска  ;
;
· плотность материала диска  ;
;
· модуль упругости материала диска  .
.
В ходе экспериментальных исследований изгибные колебания диска возбуждались с помощью пьезоэлектрического преобразователя. Форма изгибных колебаний исследовалась путем наблюдения фигур Хладни. Путем подстройки частоты возбуждения преобразователя на поверхности диска были получены фигуры Хладни с 12 и 22 радиальными узловыми линиями, что соответствует модам 6-го и 11-го порядка. Соответствующие частоты возбуждения были измерены с помощью электронносчетного частотомера ЧЗ-33 и составляли 14,00 кГц и 21,27 кГц. При этом для моды 6-го порядка наблюдалась одна узловая окружность. Для моды 11-го порядка узловые окружности отсутствовали. Таким образом, результаты экспериментальных исследований для моды 6-го порядка хорошо согласуются с теоретическими расчетами. Для моды 11-го порядка величина погрешности более значительна, однако она является приемлемой для выполнения предварительных оценок. Фотографии фигур Хладни, соответствующих модам 6-го и 11-го порядка, приведены на рисунке 3.
а) |
| б) |
|
Рисунок 3 – Фотографии фигур Хладни на поверхности ограночного диска:
а) мода 6-го порядка; б) мода 11-го порядка
Выводы. Результаты сравнения расчетных значений собственных частот с экспериментальными данными показывают, что для мод небольшого порядка теоретическая модель имеет хорошую точность. С возрастанием порядка моды погрешность теоретических расчетов увеличивается, однако остается приемлемой для выполнения предварительных оценок. Более точные расчеты могут быть выполнены с помощью метода конечных элементов (в частности, с помощью модального анализа в пакете ANSYS).
СПИСОК ЛИТЕРАТУРЫ
1. Киселев применения ультразвука для шаржирования ограночных дисков методом укатки / , , // Теоретические и технологические основы упрочнения и восстановления изделий машиностроения: Сб. науч. трудов / Под ред. , . – Мн., 2001. – С. 626-629.
2. Бабаков колебаний / . 3-е изд. – М.: Наука. Гл. ред. физ.-мат. лит., 1968. – 560 с.
3. Математика для электро - и радиоинженеров / А. Анго. – М.: Наука. Гл. ред. физ.-мат. лит., 1965. – 780 с.






