Основы логического и функционального программирования (стр. 3 )

Результат работы программы: 3 в степени 2=9

Как видно, рекурсивные задачи, решаемые с помощью Prolog’а, отличаются краткостью и приближенностью к естественному языку.

Но таким образом организованная рекурсия имеет один, но существенный недостаток. При достаточно глубокой рекурсии переполняется стек вызовов, и выполнение программы аварийно завершается. Можно ли избежать такой ситуации? Да, это возможно, при специальным образом организованной рекурсии. Такая рекурсия называется хвостовой. Прежде чем перейти к рассмотрению хвостовой рекурсии, рассмотрим для начала следующий пример.

Предположим, имеются некоторые абстрактные процедуры F1, F2, F3 и F4. Пусть в процессе выполнения процедуры F1 выполняется вызов процедуры F2, при выполнении которой, в свою очередь, вызывается процедура F3, которая, в свою очередь, вызывает F4. В этом случае стек вызовов будет выглядеть следующим образом:

Сохранять состояние вызывающей процедуры необходимо для того, чтобы продолжить ее выполнение после завершения вызова. Но, а если вызов процедур F2, F3 и F4 будет последним действием в вызывающих процедурах? Тогда можно не сохранять состояние вызывающей процедуры, так как в ней после завершения вызова больше ничего выполняться не будет. Можно хранить в стеке вызовов только состояние последней вызванной процедуры, другими словами подменять состояние бывшей процедуры состоянием новой процедуры.

То есть считать, что процедура F1 вызывает процедуру F4 непосредственно. В этом случае, не расходуется стек вызовов.

Теперь перейдем к варианту с рекурсивными вызовами процедур. Пусть в процессе выполнения процедуры F1 выполняется вызов процедуры F2, при выполнении которой, в свою очередь, рекурсивно вызывается процедура F2, которая, в свою очередь, вновь рекурсивно вызывает саму себя, то есть опять вызывает F2. В этом случае стек вызовов будет хранить только состояние последнего рекурсивного вызова, то есть стек вновь не будет переполняться!

Выполнение таким образом организованной рекурсии не будет завершаться аварийно из-за переполнения стека, сколько бы ни было рекурсивных вызовов! Аварийное завершение по другим причинам, конечно, не исключается.

Можно на практике убедиться, что это действительно так. Попробуйте запустить следующую программу и посмотреть, в течение какого времени она будет благополучно работать:

PREDICATES

tail_recursion

CLAUSES

%хвостовая рекурсия

tail_recursion:- write (“*”), tail_recursion.

GOAL

tail_recursion.

Теперь можно сформулировать условия, при соблюдении которых рекурсия в Prolog’е становится хвостовой, то есть не расходует стек при неограниченном количестве рекурсивных вызовов:

1. рекурсивный вызов должен быть последней целью в хвостовой части правила вывода.

2. перед рекурсивным вызовом не должно быть точек возврата (это условие хвостовой рекурсии специфично для Prolog’а).

Если первое условие очевидно, то необходимость выполнения второго условия может быть, на первый взгляд, не совсем понятна. Чтобы рекурсия была хвостовой, необходимо, чтобы доказательство рекурсивного вызова было действительно последним действием в хвостовой части правила. А если до рекурсивного вызова имеется цель, которую можно передоказать, то есть имеется точка возврата? Тогда придется сохранять в стеке состояние вызывающего правила! Вдруг в дальнейшем, где-то в глубинах рекурсии какая-либо цель не будет доказана? Тогда будет включен поиск с возвратом к ближайшей точке возврата, для чего и нужно сохранять состояние в стеке соответствующего правила (чтобы знать, куда вернуться).

Если соблюдение первого условия сложности не представляет (легко проконтролировать, чтобы рекурсивный вызов был последней целью в теле правила), то как быть уверенным в соблюдении второго условия, в отсутствии точек возврата до рекурсивного вызова?

Соблюсти второе условие очень просто. Достаточно перед рекурсивным вызовом поставить отсечение. Только и всего! Конечно, использовать отсечение следует как можно раньше в теле правила, но, в крайнем случае, его можно использовать в качестве предпоследней цели (последняя цель, естественно, рекурсивный вызов)

Примеры нехвостовой рекурсии и ее преобразования в хвостовую:

%пример нехвостовой рекурсии

PREDICATES

counter (integer)

CLAUSES

counter (N):- write (“N=”, N), nl, New_N=N+1, counter (New_N), nl.

GOAL

counter (0).

Естественно, приведенный пример не является примером хвостовой рекурсии, однако получить хвостовую рекурсию достаточно просто: нужно всего лишь убрать цель nl (переход на новую строчку) после рекурсивного вызова.

%пример хвостовой рекурсии

PREDICATES

counter (integer)

CLAUSES

%выполнение программы аварийно завершится из-за переполнения

%разрядной сетки для integer, но не из-за переполнения стека

counter (N):- write (“N=”, N), nl, New_N=N+1, counter (New_N).

GOAL

counter (0).

В рассмотренном примере соблюдены оба условия хвостовой рекурсии: рекурсивный вызов последний в теле правила и нет точек возврата перед рекурсивным вызовом. Действительно, цели write (“N=”, N), nl и New_N=N+1 передоказать нельзя, соответственно, нет и точки возврата.

%пример нехвостовой рекурсии

PREDICATES

counter (integer)

CLAUSES

counter (N):- N>0, write (“N=”, N), nl, New_N=N–1, counter (New_N).

counter (N):- write (“Отрицательное N=”, N).

GOAL

counter (1000).

В приведенном примере рекурсия хвостовой не является из-за оставленной точки возврата. Пока N будет положительным, для доказательства рекурсивной подцели будет использоваться первое правило вывода, но ведь остается неиспользованным второе правило, что и дает точку возврата. Преобразовать нехвостовую рекурсию в хвостовую можно, убрав точку возврата с помощью отсечения. Первое правило нужно переписать следующим образом:

counter (N):- N>0, !, write (“N=”, N), nl, New_N=N–1, counter (New_N).

Если N – положительное число, второе правило заведомо не понадобится.

%пример хвостовой рекурсии

PREDICATES

counter (integer)

CLAUSES

counter (N):- N>0, !, write (“N=”, N), nl, New_N=N–1, counter (New_N).

counter (N):- write (“Отрицательное N=”, N).

GOAL

counter (1000).

%пример нехвостовой рекурсии

PREDICATES

counter (integer)

check (integer)

CLAUSES

counter (N):- check (N), write (“N=”, N), nl, New_N=N–1, counter (New_N).

check (N):- N>0, write (“Положительное ”).

check (_):- write (“Отрицательное ”).

GOAL

counter (1000).

В приведенном примере рекурсия также хвостовой не является вновь из-за оставленной точки возврата. Пока N будет положительным, для доказательства рекурсивной подцели будет использоваться первое правило вывода для предиката check, но ведь остается неиспользованным второе правило для того же самого предиката, что и дает точку возврата. Преобразовать нехвостовую рекурсию в хвостовую можно, убрав точку возврата с помощью отсечения, как и в первом примере. Первое правило для предиката counter можно переписать следующим образом:

counter (N):- check (N), !, write (“N=”, N), nl, New_N=N–1, counter (New_N).

Но более правильно, с точки зрения хорошего стиля программирования на Prolog’е, точку возврата лучше убрать в предложении для предиката check.

%пример хвостовой рекурсии

PREDICATES

counter (integer)

check (integer)

CLAUSES

counter (N):- check (N), write (“N=”, N), nl, New_N=N–1, counter (New_N).

check (N):- N>0, !, write (“Положительное ”).

check (_):- write (“Отрицательное ”).

GOAL

counter (1000).

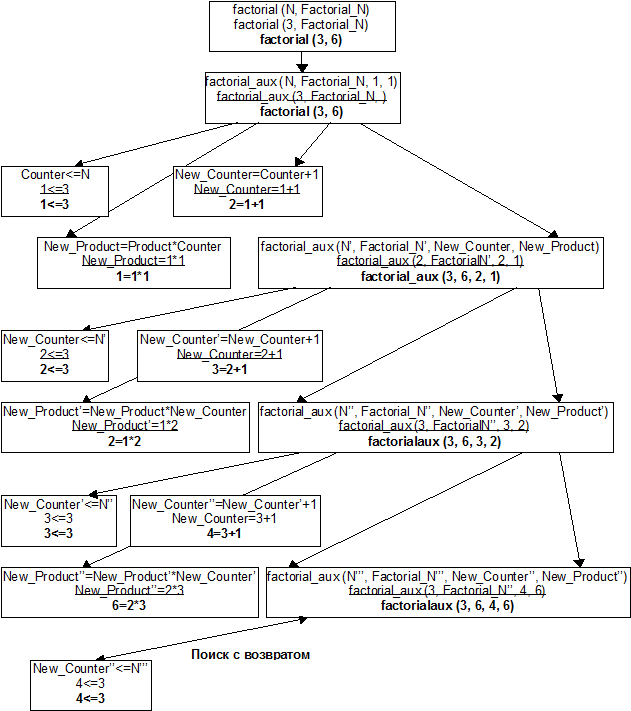
Не всегда так легко и просто можно преобразовать нехвостовую рекурсию в хвостовую. Иногда для этого требуется полностью переписать программу. Рассмотрим уже известный пример вычисления факториала. Рекурсия в приведенном ранее примере, очевидно, хвостовой не является. Только с помощью применения отсечения добиться хвостовой рекурсии нельзя. Придется полностью преобразовать программу.

Пример: вычисление n! с применением хвостовой рекурсии.

PREDICATES

factorial (integer, integer)

factorial_aux (integer, integer, integer, integer)

CLAUSES

factorial (N, Factorial_N):- factorial_aux (N, Factorial_N, 1, 1).

factorial_aux (N, Factorial_N, Counter, Product):- Counter<=N, !,
New_Product=Product*Counter, New_Counter=Counter+1,
factorial_aux (N, Factorial_N, New_Counter, New_Product).

factorial_aux (_, Factorial_N, _, Factorial_N).

GOAL

write (“Для какого числа Вы хотите найти факториал? ”), readint (Number),

factorial (Number, Result), write (Number, “!=”, Result).

В данном случае при организации рекурсии были использованы вспомогательный предикат factorial_aux с четырьмя параметрами. Переменные N и Factorial_N служат для тех же целей, что и в примере с нехвостовой рекурсией, переменная N конкретизируется значением, для которого нужно вычислить факториал, Factorial_N – собственно полученный результат. Переменные Counter и Product – вспомогательные, Counter – счетчик рекурсивных вызовов, Product – постепенно накапливающийся результат.

Рассмотрим более подробно работу программы. Единственное предложение для предиката factorial служит для того, чтобы перейти от предиката с двумя параметрами к вызову предиката с четырьмя параметрами. Первое предложение для предиката factorial_aux выполняет основные вычисления. При этом результат постепенно формируется при выполнении рекурсивных вызовов и достигает нужного значения в момент, когда текущий счетчик Counter становится больше значения N. В этот момент переменная Product конкретизируется значением готового результата, то есть в момент, когда рекурсия должна быть остановлена, значение факториала уже рассчитано.

В приведенном примере результат готов в тот момент, когда условие Counter<=N более не выполняется (соответственно цель Counter<=N не доказывается), переменная Product конкретизируется значением рассчитанного факториала. Теперь необходимо передать полученное значение из четвертого параметра во второй. Для этого служит второе предложение для предиката factorial_aux. Цель Counter<=N не доказывается и выполняется поиск с возвратом ко второму предложению для предиката factorial_aux. Использование одноименных переменных для второго и четвертого параметров в этом предложении как раз и обеспечивает переприсваивание полученного значения. Все, что теперь остается сделать – это передать полученное значение факториала из рекурсивных вызовов, никак не изменяя его.

Следует отметить применение отсечения в первом предложении для предиката factorial_aux. Отсечение в данном случае служит для того, чтобы убрать точку возврата, если цель Counter<=N успешно доказывается, соответственно второе предложение для предиката factorial_aux использовано заведомо не будет. Во втором предложении также нет проверки условия Counter>N, так как это излишне. Переход ко второму предложению будет выполнен, только если Counter будет больше, чем N. В качестве первого и третьего параметров используются анонимные переменные, так как в данном случае не важно ни значение переменной N, ни значение текущего счетчика Counter.

Второе предложение можно переписать в более подробном варианте,

factorial_aux (_, Factorial_N, _, Product):- Factorial_N=Product.

однако так, как это предложение записано в примере выше, с точки зрения стиля программирования на Prolog’е, будет более грамотно.

Дерево целей для случая вычисления факториала 3!.

Составные объекты

Составные объекты данных позволяют рассматривать информацию, состоящую из нескольких частей, как единое целое, в то же время предоставляя возможность получать доступ к отдельным частям этой информации.

Например, дата рождения человека может быть представлена как единый объект, и в то же время, дата состоит из трех частей, числа, месяца и года. Такую составную структуру можно представить как единое целое, использовав функтор, например, birthday. Имя функтора выбирается произвольно. Тогда структура будет выглядеть следующим образом:

birthday (25, “мая”, 1980)

Секция описания доменов будет выглядеть следующим образом:

DOMAINS

day=birthday (integer, symbol, integer)

Такое описание домена позволит определить предикат, в котором в качестве аргумента можно использовать данные, принадлежащие домену day. Далее следует пример программы с использованием данного домена.

DOMAINS

day=birthday (integer, string, integer)

name=string

PREDICATES

congratulation (name, day)

print

print2

CLAUSES

congratulation (“Анна”, birthday (25, “мая”, 1980)).

congratulation (“Иван”, birthday (17, “декабря”, 1957)).

congratulation (“Петр”, birthday (30, “июля”, 2001)).

print:- congratulation (Name, birthday (Day, Month, Year)), write (“С днем рождения ”, Day, Month, Year, ”, ”, Name,”!”), nl, fail.

print.

print2:- congratulation (Name, Birthday), write (“С днем рождения ”, Birthday, ”, ”, Name,”!”), nl, fail.

print2.

GOAL

print, print2.

Как видно из вышеприведенного примера, к составному объекту можно обратиться как единому целому, так и получить доступ к его составным элементам.

Списки

Список – это объект, который содержит конечное число других объектов. Список в Prolog’е можно приблизительно сравнить с массивами в других языках, но для списков нет необходимости заранее объявлять размерность.

Список в Prolog’е заключается в квадратные скобки, и элементы списка разделяются запятыми. Список, который не содержит ни одного элемента, называется пустым списком.

Примеры списков:

список, элементами которого являются целые числа

[1, 2, 3]

список, элементами которого являются символы

[one, two, three]

список, элементами которого являются строки

[“One”, “Two”, “Three”]

пустой список

[ ]

Для работы со списками с Prolog’е не существует отдельного домена, для того, чтобы работать со списком, необходимо объявить списочный домен следующим образом:

DOMAINS

listdomain=elementdomain*

elementdomain=…

listdomain – это произвольно выбранное имя нестандартного списочного домена, elementdomain – имя домена, которому принадлежит элемент списка, звездочка * как раз и обозначает, что выполнено объявление списка, состоящего из элементов домена element. При работе со списками нельзя включать в список элементы, принадлежащие разным доменам. В таком случае нужно воспользоваться составным доменом.

Примеры объявления списочных доменов:

DOMAINS

%элементы списка – целые числа

intlist=integer*

%элементы списка – символы

symlist=symbol*

%элементы списка – строки

strlist=string*

%элементы списка – или целые числа, или символы, или строки

mixlist=mixdomain*

mixdomain=int(integer); sym(symbol); str(string)

Обратите внимание, что при объявлении составного домена были использованы функторы, так как объявление вида mixdomain=integer; symbol; string привело бы к ошибке.

Список является рекурсивным составным объектом, состоящим из двух частей. Составные части списка:

3. Голова списка – первый элемент списка;

4. Хвост списка – все последующие элементы, являющиеся, в свою очередь списком.

Примеры голов и хвостов списков:

[1, 2, 3] голова списка – 1, хвост списка – [2, 3]

[1] голова списка – 1, хвост списка – [ ]

[ ] пустой список нельзя разделить на голову и хвост

В Prolog’е используется специальный символ для разделения списка на голову и хвост – вертикальная черта |.

Например:

[1, 2, 3] или [1 | [2, 3]] или [1 | [2| [3]]] или [1 | [2 | [3 | [ ]]]]

[1] или [1 | [ ]]

Вертикальную черту можно использовать не только для отделения головы списка, но и для отделения произвольного числа начальных элементов списка:

[1, 2, 3] или [1, 2 | [3]] или [1, 2, 3 | [ ]]

Примеры сопоставления и унификации в списках:

[1, 2, 3]=[Elem1, Elem2, Elem3] Elem1=1, Elem2=2, Elem3=3

[1, 2, 3]=[Elem1, Elem2, Elem3 | T] Elem1=1, Elem2=2, Elem3=3, T=[ ]

[1, 2, 3]=[Head | Tail] Head=1, Tail=[2, 3]

[1, 2, 3]=[Elem1, Elem2 | T] Elem1=1, Elem2=2, T=[3]

[1, 2, 3]=[4 | T] ошибка

[ ]=[H | T] ошибка

Так как список является рекурсивной структурой данных, то для работы со списками используется рекурсия. Основной метод обработки списков заключается в следующем: отделить от списка голову, выполнить с ней какие-либо действия и перейти к работе с хвостом списка, являющимся в свою очередь списком. Далее у хвоста списка отделить голову и так далее до тех пор, пока список не останется пустым. В этом случае обработку списка необходимо прекратить. Следовательно, предикаты для работы со списками должны иметь, по крайней мере, два предложения: для пустого списка и для непустого списка.

Пример: поэлементный вывод списка, элементами которого являются целые числа, на экран (нужно отметить, что этот пример приводится в учебных целях, список вполне может быть выведен на экран как единая структура, например, GOAL List=[1, 2, 3], write(List)).

DOMAINS

intlist=integer*

PREDICATES

printlist (intlist)

CLAUSES

%если список пустой, то выводить не экран нечего

printlist ([ ]):- !.

%если список непустой, то отделить от списка голову, напечатать ее и

%использовать тот же самый предикат для печати хвоста списка, то есть

%выполнить рекурсивный вызов предиката printlist, передав в качестве

%аргумента хвост

printlist ([H | T]):- write (H), nl, printlist (T).

GOAL

printlist ([1, 2, 3]).

Результат работы программы:

1

2

3

Еще один пример работы со списком – подсчет числа элементов списка или, другими словами, определение длины списка. Для того чтобы определить длину списка, вновь нужно рассмотреть два случая: для пустого и непустого списков. Если список пуст, то его длина равна 0, если же список не пуст, то определить его длину можно следующим образом: разделить список на голову и хвост, подсчитать длину хвоста списка и увеличить длину хвоста на единицу (то есть учесть отделенную предварительно голову списка.)

DOMAINS

intlist=integer*

PREDICATES

list_length (intlist, integer)

CLAUSES

%если список пустой, то его длина равна 0

list_length ([ ], 0):- !.

%если список непустой, то его длина равна длине хвоста, увеличенной на 1

list_length (List, Length):- List=[H | T], list_length (T, Length_T), Length=Length_T+1.

%более кратко второе правило вывода можно записать, перенеся разделение

%списка на голову и хвост в заголовок предложения и избавиться от лишней

%переменной List

%list_length ([H | T], Length):- list_length (T, Length_T), Length=Length_T+1.

GOAL

listlength ([1, 2], Length), write(“Length=”, Length).

Результат работы программы:

Length=2

Для того чтобы лучше понять, каким образом работает приведенный пример, удобно воспользоваться деревом целей. В данном примере следует обратить внимание на то, каким образом формируется выходное значение – длина списка. Счетчик для подсчета числа элементов в списке обнуляется в момент, когда рекурсия останавливается, то есть список разбирается до пустого списка-хвоста и результат насчитывается при выходе из рекурсии.

Достаточно часто необходимо обработать список поэлементно, выполняя некоторые действия с элементами списка, в зависимости от соблюдения некоторых условий. Предположим, необходимо преобразовать список, элементами которого являются целые числа, инвертируя знак элементов списка, то есть положительные числа преобразовать в отрицательные, отрицательные в положительные, для нулевых значений никаких действий не предпринимать. Вновь придется рассмотреть два случая – для непустого и пустого списков. Преобразование пустого списка дает в результате такой же пустой список. Если же список не пуст, то следует рекурсивно выполнять отделение головы списка, ее обработку и рассматривать полученный результат как голову списка-результата.

DOMAINS

intlist=integer*

PREDICATES

inverting (intlist, intlist)

processing (integer, integer)

CLAUSES

%обработка пустого списка дает, в результате, тоже пустой список

inverting ([ ], [ ]):- !.

%если список непустой, отделить голову, обработать ее,

%и добавить в качестве головы списка-результата

inverting ([H | T], [Inv_H | Inv_T]):- processing (H, Inv_H), inverting (T, Inv_T).

%предикат processing выполняет действия по обработке элемента списка в

%зависимости от его знака, предикат имеет два предложения, так как нужно

%рассмотреть два варианта: ненулевое и нулевое значения

processing (0, 0):- !.

processing (H, Inv_H):- Inv_H=-H.

GOAL

inverting ([-2, -1, 0, 1, 2], Inv_List), write(“Inv_List=”, Inv_List).

Результат работы программы:

Inv_List=[2, 1, 0, -1, -2]

Следующий пример рассматривает достаточно часто встречающуюся задачу – определение принадлежности элемента списку. Проверка принадлежности элемента списку выполняется достаточно просто – отделением головы списка и сравнением ее с искомым элементом. Если сравнение завершилось неудачей, продолжается поиск элемента в хвосте списка. Признаком наличия искомого элемента в списке будет успешное доказательство цели, если же цель не была доказана, значит, такого элемента в списке нет.

DOMAINS

strlist=string*

PREDICATES

member (string, strlist)

search (string, strlist)

CLAUSES

%искомый элемент найден, его значение совпало со значением головы списка,

%хвост списка обозначен анонимной переменной, так как теперь хвост списка

%не важен

member (Elem, [Elem | _]):- !.

%если элемент пока не обнаружен, попробовать найти его в хвосте списка,

%теперь для головы списка использована анонимная переменная, поскольку ее

%значение не важно, так как оно точно не равно искомому значению

member (Elem, [_ | T]):- member (Elem, T).

%предикат search служит для двух целей: во-первых, чтобы сообщить о

%результатах поиска, и, во-вторых, чтобы при любом исходе поиска программа

%всегда заканчивала свое выполнение с успехом

search (Elem, List):- member (Elem, List), !, write (“Элемент найден! :-) ”).

search (_, _):- write (“Элемент не найден! :-( ”).

GOAL

Cityes=[“Москва”, “Санкт-Петербург”, “Омск”, “Новосибирск”, “Томск”], City=“Новосибирск”, search (City, Cityes).

Результат работы программы:

Элемент найден! :-)

Последний пример, который будет рассмотрен, это решение задачи соединения двух списков. Итак, каким образом можно объединить два списка? Предположим, имеется два двухэлементных списка: [1, 2] и [3, 4]. Объединение нужно начать с последовательного отделения голов первого списка до тех пор, пока первый список не станет пустым. Как только первый список станет пустым, его легко можно будет объединить со вторым, непустым, никоим образом к этому моменту не изменившимся списком. В результате, естественно, будет получен список, полностью совпадающий со вторым. Все, что осталось сделать, это добавить головы, отделенные от первого списка, ко второму списку. Вот как это выглядит в пошаговом описании:

1. отделяется голова от первого списка – [1, 2] –> [1 | [2]] (голова – 1, хвост – [2])

2. продолжается выполнение отделение головы, только теперь от полученного хвоста – [ 2] –> [2 | [ ]] (голова – 2, хвост – [ ])

3. когда первый список разобран до пустого, можно приступить к его объединению со вторым, непустым списком, объединяются пустой хвост [ ] и непустой второй список [3, 4] – получается тоже непустой список – [3, 4], теперь можно приступать к формированию объединенного списка, так как основа для списка-результата заложена, это его будущий хвост – [3, 4]

4. к хвосту списка-результата [3, 4] добавляется последняя отделенная от первого списка голова 2, что дает следующий список – [2, 3, 4]

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4