Четырёхкратные интегралы, представимые в виде линейных форм от значений дзета – функции римана

УДК 511. 36

,

четырёхкратные интегралы, представимые в виде линейных форм от значений дзета – функции Римана

Рассмотрены преобразования интеграла и получена его групповая структура.

Ключевые слова: четырехкратные интегралы; линейные формы; дзета-функция Римана; групповая структура.

Исследование групповой структуры является важным элементом получения оценки меры иррациональности значений дзета – функции Римана в целых точках. Групповые преобразования были использованы Рином и Виолой [8] для улучшения оценки меры иррациональности ζ(3).

После того как в 1882 г. Линдеманн [7] доказал, что π – число трансцендентное, стало ясно, что для, , значения дзета – функции Римана являются трансцендентными числами.

После доказательства Апери [2] иррациональности ζ(3) Бейкерс в 1979 г. предложил доказательство этого факта с помощью интеграла 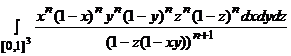. Также Бейкерсом [3] был рассмотрен интеграл , с помощью которого может быть доказана иррациональность ζ(2). Этот факт был известен ранее, но с помощью интеграла Бейкерса и иного выбора параметров была улучшена оценка иррациональности π2. Были также предприняты различные попытки обобщения интегралов Бейкерса для изучения дзета – функции Римана в целых точках. В 1990 г. [4] рассмотрел интеграл

(1)

который при m = 2 совпадает с интегралом Бейкерса. [5] доказал, что при m = 4 интеграл (1) представим виде линейных форм с рациональными коэффициентами.

В 1998 г. [9] вёл в рассмотрение интеграл вида

(2)

Интеграл (2) равен интегралу Бейкерса. Это было доказано С. Фишлером [10] и С. Злобиным [6].

Ранее [1] был рассмотрен четырёхкратный интеграл типа интеграла (1), для которого была получена групповая структура.

Рассмотрим обобщенный интеграл типа интеграла (2) с произвольным набором параметров, а именно интеграл вида

, (3)

где .

Преобразования в интеграле. Лемма. Пусть в интеграле

I = A > 0, B+A > 0; a, b, с N; I = I(a, b,c). Тогда справедливы следующие формулы:

; (4)

; (5)

=

.

В основе групповой структуры интеграла (3) лежат пять преобразований: g1, g2, g3, g4, g5. Рассмотрим каждое из них.

1. Преобразование g1 может быть получено применением к интегралу (3) формулы (5) леммы по переменной x = x4. Оно позволяет получить интеграл вида

,

где , т. е..

2. Проведя в интеграле (3) преобразование по формуле (5) леммы по переменной x1, получаем g2, такое, что , где .

3. В интеграле (3) сделаем замену переменных:

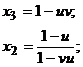
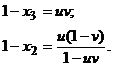
Аналогичную замену проводили Рин и Виола [7]. В результате интеграл принимает вид . (6)

Сделав преобразование симметрии между интегралами (3) и (6), которое переводит переменные получаем преобразование g3: .

4. Применяя к интегралу (3) формулу (5) по переменной x2, получаем преобразование g4: , где .

5. И, наконец, применение к интегралу (3) формулы (4) леммы по переменной x = x4 даёт преобразование g5, такое, что

.

Групповая структура интеграла. Представим интеграл (3) в виде интеграла от переменных:

,

где a1 = ω1; b1 = ω2; a2 = ω3; b2 = ω4; a4 = ω5; b3 = ω6; b4 = ω7; α2 = ω8; α1 = ω9.

Введём следующие параметры:

ω10 = ω6 + ω7 – ω8, ω11 = ω1 + ω2 – ω9, ω12 = ω3 + ω2 – ω9, ω13 = ω3 + ω4 – ω9, ω14 = ω3 +

+ ω4 – ω1, ω15 = ω7 + ω5 – ω8, ω16 = ω5 + ω4 – ω8, ω17 = ω5 + ω4 – ω6, ω18 = ω5 + ω4 + ω3 – ω8 –

– ω9, ω19 = ω5 + ω3 + ω4 – ω6 – ω9, ω20 = ω4 + ω3 + ω5 – ω1 – ω8, ω21 = ω3 + ω4 + ω5 – ω1 – ω6.

Рассмотрим каждое из преобразований интеграла относительно параметров ω1, ω2, ω3, … , ω21. Преобразование g1:

ω1' = ω1, ω2' = ω2, ω3' = ω3, ω4' = ω4; ω5' = ω5, ω6' = ω8, ω7' = ω6 +ω7 –ω8 = ω10, ω8' = ω6, ω9' = = ω9, ω10' = ω6 + ω7 + ω8 – ω8 – ω6 = ω7, ω11' = ω11, ω12' = ω2 + ω3 – ω9 = ω12, ω13' = ω3 +ω4 –ω9 = = ω13, ω14' = ω14, ω15' = ω15, ω16' = ω4 + ω5 – ω6 = ω17, ω17' = ω4 + ω6 – ω8 = ω16, ω18' = ω3 + ω4 + + ω5 – ω6 – ω9 = ω19, ω19' = ω5 + ω4 + ω3 – ω8 – ω9= ω18, ω20' = ω3 + ω4 + ω5 – ω1 – ω6 = ω21,

ω21' = ω3 + ω5 + ω4 – ω1 – ω8 = ω20.

Таким образом, g1: (ω6, ω8)(ω7, ω10)(ω16, ω17)(ω18, ω19)(ω20, ω21).

Рассмотрев аналогично преобразования g2, g3, g4, g5, получаем:

g2: (ω1, ω9)(ω2, ω11)(ω13, ω14)(ω18, ω20)(ω19, ω21);

g3: (ω1, ω6)(ω2, ω7)(ω3, ω5)(ω8, ω9)(ω10, ω11)(ω12, ω15)(ω13,ω16)(ω14, ω17)(ω19, ω20);

g4: (ω2, ω12)(ω3, ω9)(ω4, ω13)(ω16, ω18)(ω17, ω19);

g5: (ω5, ω15)(ω6, ω7)(ω8, ω10)(ω16, ω17)(ω18, ω19)(ω20, ω21).

Все возможные комбинации этих преобразований образуют группу G, состоящую из 288 элементов.

Создадим массив, элементы которого – параметры ω1, ω2, ω3, … , ω21. Сохраняем этот массив. Применяем поочерёдно к этому массиву преобразования g1, g2, g3, g4, g5. Получаем 5 новых массивов, отличных от исходного. Добавляем эти 5 массивов к сохранённому.

К каждому из сохранённых массивов применяем преобразования g1, g2, g3, g4, g5 (поочерёдно). Полученные массивы сравниваем с уже имеющимися, и если рассматриваемый массив отличен от всех сохранённых, добавляем его к ним. Повторяя это действие (применение преобразований к сохранённым массивам) до тех пор, пока после применения преобразований не появится ни одного массива, отличного от уже имеющихся, получим 288 массивов (это произойдёт на 9 шаге, т. е. любой набор параметров, получаемый путём применения 9 преобразований, уже был получен ранее с помощью меньшего количества преобразований).

Данный алгоритм позволяет получить комбинацию минимального количества преобразований для каждого возможного набора параметров. При этом все остальные комбинации преобразований будут давать всё те же наборы параметров, но используя большее количество преобразований.

Функция

является инвариантной относительно всех преобразований этой группы.

Таким образом, для gÎG

,

.

СПИСОК ЛИТЕРАТУРЫ

1. Андросенко, структура четырёхкратного интеграла / , // Вестн. БГТУ. – 2006. – №4. – С. 122 – 125.

2. Apery, R. Irrationalite de z(2) et z(3) /R. Apery// Asterisque 61. – 1979. – P. 11 – 13.

3. Beukers, F. A note on the irrationality of z(2) and z(3) F. Beukers// Bull. Lond. Math. Soc. 11. – 1978. – № 33. – P. 268 – 279.

4. Василенко, формулы для значений дзета – функции Римана в целых точках / //Республик. науч. – теорет. конф. «Теория чисел и её приложения», 26 – 28 сент. 1990 г.: тез. докл. - Ташкент: Ташкент. гос. пед. ин – т, 1990. – С. 27.

5. Васильев, формулы для значений дзета – функции Римана в целых точках / // Вестн. МГУ. Сер. 1. Математика, механика. – 1996. – №1 – С. 81 – 84.

6. Злобин, С. А. О некоторых интегральных тождествах / // Успехи математических наук. – 2002. – Т. 53. – № 3. – С. 153 – 154.

7. Lindemann, F. Uber die Zalh p / F. Lindemann// Math. Annalen 20. – 1882. – P. 213 – 235.

8. Rhin, G. The group structure for z(3) / G. Rhin, C. Viola// Acta Arith. 97. – 2001. – № 3. – P. 269 – 293.

9. Сорокин, Апери / // Вестн. МГУ. Сер. 1. Математика, механика. – 1998. – № 3. – С. 48 – 52.

10. Fischler, S. Formes lineaires en polyzetas et integrals multiples / S. Fischler// C. R. Acad. Sci. Paris Ser. 1. Math. – 2002. – V. 335. – P. 1 – 4.

Материал поступил в редколлегию 05.12.07.