Тема: «Сложение и вычитание алгебраических дробей с разными знаменателями»

Предметы точных дисциплин (алгебра)

Айшаева Фердаус Сулеймановна

Учитель математики и информатики

МКОУ СОШ с. п.Кара-Суу

Цели и задачи:

Образовательные: сформировать у учащихся умение приводить алгебраические дроби к общему знаменателю и выполнять их сложение и вычитание; повторить и закрепить действия сложения и вычитания дробей с одинаковыми знаменателями, способы разложения многочлена на множители, сокращение дробей.

Воспитательные: воспитывать у учащихся интерес к алгебре, применяя интересные задания, различные формы работы; формирование личностных качеств: точность и ясность словесного выражения мыслей, сосредоточенность и внимание, ответственность и настойчивость.

Развивающие: развивать у учащихся умение работать как индивидуально (самостоятельно), так и коллективно (работа в парах); развивать познавательные интересы.

Оборудование: компьютер, проектор, карточки с заданиями, карточки для проверки.

Задания для актуализации знаний:

1) ; 2) ;

3) 4) ; 5)

Алгоритм сложения и вычитания обыкновенных дробей с разными знаменателями.

1.  Чтобы сложить или вычесть обыкновенные дроби с разными знаменателями, надо:

·  Привести данные дроби к наименьшему общему знаменателю.

·  Сложить или вычесть полученные дроби.

2.  Алгоритм приведения алгебраических дробей к общему знаменателю.

·  Раскладываем все знаменатели на множители.

·  Из первого знаменателя выписываем произведение всех его

множителей, из остальных знаменателей приписать к этому произведению недостающие множители. Полученное произведение и будет общим (новым) знаменателем.

·  Найдём дополнительные множители для каждой из дробей: это

будут произведения тех множителей, которые имеются в общем (новом) знаменателе, но которых нет в старом знаменателе.

·  Умножим и числители, и знаменатели каждой дроби на

дополнительный множитель и получим новые дроби с общим знаменателем.

3.  Запишем каждую дробь с новым числителем и общим (новым) знаменателем.

Карточки к самостоятельной работе с взаимопроверкой:

a)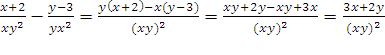

b)

Карточка для этапа рефлексии.

1.  Данная тема мне понятна.

2.  Я научился, как находить дополнительные множители к каждой из дробей.

3.  Я научился находить новые числители для каждой из дробей.

4.  В самостоятельной работе у меня всё получилось.

5.  Я смог понять причину ошибки, которую допустил в самостоятельной работе.

6.  Я доволен своей работой на уроке.

ХОД УРОКА

1. Самоопределение к деятельности.

Цели этапа:

1.  Включение учащихся в учебную деятельность: продолжение путешествия по стране “Алгебраические выражения”.

2.  Определение содержательных рамок урока: продолжение работать с алгебраическими дробями.

Организация учебного процесса на этапе 1:

- Доброе утро, ребята! Мы продолжаем наше увлекательное путешествие по стране “Алгебраические дроби с разными знаменателями ”.

- С какими “жителями” страны мы встречались на предыдущих уроках? (С алгебраическими выражениями.)

- Что мы можем выполнять с алгебраическими выражениями? (Сложение и вычитание.)

- Какая характерная особенность алгебраических дробей, которые мы уже умеем складывать и вычитать? (Мы складываем и вычитаем дроби, имеющие одинаковые знаменатели.)

- Верно. Но мы все вместе хорошо понимаем, что навыков выполнения действий с алгебраическими дробями, имеющими одинаковые знаменатели, недостаточно. Что ещё необходимо нам научиться делать? (Выполнять действия с дробями, имеющими разные знаменатели.)

- Молодцы! Тогда продолжим наше путешествие? (Да!)

2. Актуализация знаний и фиксация затруднений в деятельности.

Цели этапа:

1.  Актуализировать знания о выполнении действий с дробями с одинаковыми знаменателями, приёмы устных вычислений.

2.  Зафиксировать затруднение.

Организация учебного процесса на этапе 2:

На доске записано несколько примеров на выполнение действий с дробями:

1) 

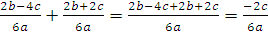
2) 

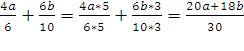
3) 

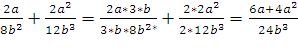
4)  =

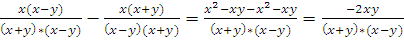
Учащимся предлагается озвучить свои варианты решения.

В первом примере ребята без труда выдают правильный ответ, вспоминая алгоритм выполнения действий с алгебраическими дробями, имеющими одинаковые знаменатели.

Когда уже прозвучал комментарий к примеру № 2, учитель акцентирует внимание на этом примере. В данном примере не только выполняются действия с алгебраическими дробями имеющими одинаковые знаменатели, но и выполняли сокращение получившейся алгебраической дроби: вынесли знак “минус” за скобки, в числителе и знаменателе получили одинаковые множители, на которые впоследствии мы и сократили результат.

Решаем задание №3

- Чем же можно воспользовался при решении примера № 3? (Алгоритмом сложения и вычитания обыкновенных дробей с разными знаменателями.)

Как именно? (Сначала надо привести алгебраические дроби к наименьшему общему знаменателю 30, а затем сложить их.)

- При решении примеров № 4 и 5 затруднение вызывает то, что эти дроби, разными знаменателями, и в состав этих разных знаменателей входят переменные (№ 4), а в № 5 вообще в знаменателях стоят буквенные выражения!..”

Ответ на задания 4–5 не получены.

3. Выявление места и причин затруднений и постановка цели деятельности.

Цели этапа:

1.  Зафиксировать отличительное свойство задания, вызвавшего затруднение в учебной деятельности.

2.  Сформулировать цель и тему урока.

Организация учебного процесса на этапе 3:

- Почему при их решении заданий №4 и 5 вы не готовы обсудить решение и дать ответ? (Потому что алгебраические дроби, предложенные в этих заданиях, имеют разные знаменатели, а нам знаком алгоритм выполнения действий с алгебраическими дробями, имеющими одинаковые знаменатели.

Что же нам ещё надо уметь делать? Надо научиться складывать и вычитать дроби с разными знаменателями.

Как можно сформулировать тему нашего сегодняшнего урока? Сложение и вычитание алгебраических дробей с разными знаменателями.

Тема урока записывается в тетрадях.

4. Построение проекта выхода из затруднения.

Цель этапа:

1.  Построение детьми нового способа действий.

2.  Фиксация алгоритма приведения алгебраических дробей к общему знаменателю.

Организация учебного процесса на этапе 4:

- Какую же цель мы сегодня поставим перед собой на уроке? (Научиться складывать и вычитать алгебраические дроби с разными знаменателями.)

- Как же быть? (Для этого мы должны построить алгоритм дальнейшей работы с алгебраическими дробями.)

- Что нам необходимо придумать для достижения цели урока? (Алгоритм приведения алгебраических дробей к общему знаменателю, чтобы потом работать по привычному нам правилу сложения и вычитания дробей с одинаковыми знаменателями.)

Работа организована в группах, каждой группе даётся лист бумаги и маркер. Учащиеся могут предложить свои варианты алгоритма в виде перечисления шагов. На работу отводится 5 минут. Группы вывешивают свои варианты алгоритма или правила, и дальше проводится анализ каждого варианта.

Один из учащихся проводит аналогию своего алгоритма с алгоритмом сложения и вычитания обыкновенных дробей с разными знаменателями.

Впоследствии этого выводится единый вариант. Он может быть таким:

1.  Раскладываем все знаменатели на множители.

2.  Из первого знаменателя выписываем произведение всех его множителей, из остальных знаменателей приписать к этому произведению недостающие множители. Полученное произведение и будет общим (новым) знаменателем.

3.  Найдём дополнительные множители для каждой из дробей: это будут произведения тех множителей, которые имеются в новом знаменателе, но которых нет в старом знаменателе.

4.  Найдём для каждой дроби новый числитель: это будет произведение старого числителя и дополнительного множителя.

5.  Запишем каждую дробь с новым числителем и общим (новым) знаменателем.

Применим наше правило для выполнения нерешённых предложенных заданий. Задания 4 и 5 решаются совместно с учителем.

5. Первичное закрепление во внешней речи.

Цель этапа:

1.  Тренировать способность к приведению алгебраических дробей к общему знаменателю.

2.  Организовать проговаривание изученного содержания правила-алгоритма во внешней речи.

Организация учебного процесса на этапе 5:

- Ребята, но все мы хорошо знаем, что просто смотреть и знать “карту местности” - это ещё не путешествие. Для того чтобы больше проникнуть в мир алгебраических дробей мы должны тренироваться в решении примеров, для того, чтобы закрепить наш новый алгоритм.

Работа с учебником:  № 000(а). (Один ученик у доски, остальные выполняют задание в тетрадях.)

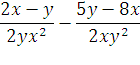
№ 000 (а, г). Учащиеся работают в парах, проговаривая решение друг другу:

a)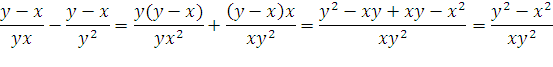

b)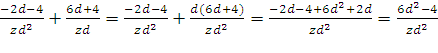

6. Самостоятельная работа с самопроверкой.

Цели этапа:

1.  Провести самостоятельную работу.

2.  Провести самопроверку по готовому эталону для самопроверки.

3.  Учащиеся зафиксируют затруднения, определяют причины ошибок и исправляют ошибки.

Организация учебного процесса на этапе 6:

На этом этапе каждый из учеников уже готов самостоятельно обдумывать способы и находить решения примеров по теме.

№ 000 (а, б): выполняют работу по вариантам.

a); b)

После выполнения работы проводится проверка по эталону. Проверяя решения, учащиеся отмечают “+” правильное решение, “?” не верное решение. Желательно, чтобы ученики, допустившие ошибки, объяснили причину, по которой они неправильно выполнили задание.

Проводится анализ и исправление ошибок.

7. Включение новых знаний в систему знаний.

Цель этапа: повторить и закрепить изученный на уроке алгоритм сложения и вычитания алгебраических дробей с разными знаменателями.

Организация учебного процесса на этапе 7:

Необходимо всегда “поддерживать связь” нового материала с пройденными темами. Поэтому предлагаются задания, для выполнения которых потребуются не только сегодня полученные знания, но и материалы ранее изученных тем.

Учащимся предлагается задания. Работа в группах:

Выполнить действия:

1) 1)

2) 2)

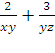
По окончанию работы представитель каждой группы выступает с получившимися результатами

Задача. Идя вдоль трамвайного пути, я заметил, что каждые 12 минут меня нагоняет трамвай, а каждые 4 минуты я сам встречаю трамвай. И я, и трамваи движемся равномерно. Через сколько минут один после другого покидают трамвайные вагоны свои конечные пункты?

Решение. Если вагоны покидают свои конечные пункты каждые x минут, то это означает, что в то место, где я встретился с одним из трамваев, через x минут приходит следующий трамвай. Если он догоняет меня, то оставшиеся 12-х минут он должен пройти тот путь, который я успеваю пройти за 12 минут. Значит, тот путь, который я прохожу за 1 минуту, трамвай проходит в минут.

Если же трамвай идет мне навстречу, то он встретит меня через 4 минуты после предыдущего, а в оставшиеся (х-4) минуты он пройдет тот путь, который я успел пройти в эти 4 минуты. Следовательно, тот путь, который я прохожу в 1 минуту, трамвай проходит в минуты. Получаем уравнение , отсюда x=6. Вагоны отходят каждые 6 минут.

8. Рефлексия урока.

Цель этапа: зафиксировать новое содержание, оценить собственную деятельность.

Организация учебного процесса на этапе 8:

- Какую цель мы поставили в начале урока? (Научиться складывать и вычитать дроби с разными знаменателями.)

- Что мы придумали для достижения цели? (Алгоритм сложения и вычитания алгебраических дробей с разными знаменателями.)

- Что мы ещё использовали при этом? (Мы раскладывали на множители знаменатели, подбирали НОК для коэффициентов, и дополнительные множители для числителей.)

Домашнее задание: параграф 4 (учебник);  № 000, 127 (задачник).