Лабораторная работа № 4
Шифры перестановки и замены
Цель работы
Освоить основные алгоритмы шифрования перестановки и замены.
Указание к работе
Ознакомиться с лекционным материалом, а также с литературой [1], [8]–[11].
Подстановочные шифры
Шифр простой подстановки.
В таком шифре производится замена каждой буквы сообщения на некоторый определенный символ (обычно также на букву).
Таким образом, сообщение  , где
, где  – последовательные буквы, переходит в шифротекст
– последовательные буквы, переходит в шифротекст ![]() , причем функция j имеет обратную функцию. Ключ является просто перестановкой алфавита (если буквы заменяются на буквы).
, причем функция j имеет обратную функцию. Ключ является просто перестановкой алфавита (если буквы заменяются на буквы).
Шифр Виженера и его варианты.
В шифре Виженера ключ задается набором из T букв. Такие наборы подписываются с повторением под сообщением и полученные две последовательности складываются по модулю, равному мощности алфавита исходного сообщения (каждая буква рассматриваемого алфавита нумеруется). Таким образом: ![]() , где
, где ![]() ,
, ![]() – мощность алфавита сообщений. Обратное преобразование:
– мощность алфавита сообщений. Обратное преобразование: 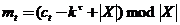 .
.
Шифр Виженера с периодом ![]() называется шифром Цезаря[1]. Он представляет собой простую подстановку, в которой каждая буква сообщения
называется шифром Цезаря[1]. Он представляет собой простую подстановку, в которой каждая буква сообщения ![]() сдвигается вперед на фиксированное число мест по алфавиту.
сдвигается вперед на фиксированное число мест по алфавиту.
Так называемый шифр Бофора и видоизмененный шифр Бофора подобны шифру Виженера. В них сообщения зашифровываются с помощью равенств ![]() и
и ![]() соответственно.
соответственно.
Повторное применение двух или более шифров Виженера будет называться составным шифром Виженера. Он имеет уравнение ![]() , где
, где ![]() вообще говоря, имеют различные периоды. Период их суммы
вообще говоря, имеют различные периоды. Период их суммы  будет наименьшим общим кратным отдельных периодов.
будет наименьшим общим кратным отдельных периодов.
Если используется шифр Виженера с неограниченным неповторяющимся ключом, то мы имеем шифр Вернама, в котором ![]() выбираются случайно и независимо среди чисел
выбираются случайно и независимо среди чисел ![]() . Если ключом служит текст, имеющий смысл, то имеем шифр «бегущего ключа».
. Если ключом служит текст, имеющий смысл, то имеем шифр «бегущего ключа».
Шифр Виженера с перемешанным один раз алфавитом представляет собой простую подстановку с последующим применением шифра Виженера: ![]() , тогда
, тогда ![]() .
.
Диграммная, триграммная и n-граммная подстановки.
Вместо подстановки одной буквы можно использовать подстановку диграмм, триграмм и т. д. Для диграммной подстановки в общем виде требуется ключ, состоящий из перестановок ![]() диграмм. Он может быть представлен с помощью таблицы, в которой ряд соответствует первой букве диграммы, а столбец – второй букве, причем клетки таблицы заполнены заменяющими символами (обычно также диграммами).
диграмм. Он может быть представлен с помощью таблицы, в которой ряд соответствует первой букве диграммы, а столбец – второй букве, причем клетки таблицы заполнены заменяющими символами (обычно также диграммами).
Имеется один метод подстановки n-грамм, который заключается в применении к последовательным n-граммам некоторой матрицы, имеющей обратную (матричная система). Предполагается, что буквы занумерованы от 0 до ![]() и рассматриваются как элементы некоторого алгебраического кольца. Если к n-грамме сообщения применить матрицу A, то получится n-грамма криптограммы:
и рассматриваются как элементы некоторого алгебраического кольца. Если к n-грамме сообщения применить матрицу A, то получится n-грамма криптограммы: 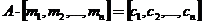 .
.
Матрица A является ключом, и расшифровка выполняется с помощью обратной матрицы: ![]() . Обратная матрица будет существовать тогда и только тогда, когда определитель
. Обратная матрица будет существовать тогда и только тогда, когда определитель ![]() имеет обратный элемент в данном кольце.
имеет обратный элемент в данном кольце.
Перестановочные шифры
Перестановка с фиксированным периодом T.
В этом случае сообщение делится на группы символов длины T и к каждой группе применяется одна и та же перестановка. Эта перестановка является ключом; она может быть задана некоторой перестановкой первых T целых чисел.
Последовательное применение двух или более перестановок будет называться составной перестановкой. Если периоды этих перестановок равны ![]() то, очевидно, в результате получится перестановка периода T, где T – наименьшее общее кратное
то, очевидно, в результате получится перестановка периода T, где T – наименьшее общее кратное ![]() .
.
Дробные шифры.
В этих шифрах каждая буква сначала зашифровывается в две (или более) буквы или в два (или более) числа, затем полученные символы каким-либо способом перемешиваются (например, с помощью транспозиции), после чего их можно снова перевести в первоначальный алфавит. После того, как полученный ряд чисел подвергнут некоторой перестановке, его можно снова разбить на пары чисел и перейти к буквам.
Пример.
Необходимо предложить вариант шифра матричной системы (триграмма). Пусть алфавит сообщений 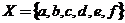 . Буква a кодируется 0,
. Буква a кодируется 0, ![]() . Надо подобрать такую матрицу A, чтобы
. Надо подобрать такую матрицу A, чтобы ![]() был равен одному из возможных значений
был равен одному из возможных значений ![]() :
:  ,
, ![]() . Сообщение для отправки:
. Сообщение для отправки: ![]() . Делим его на блоки по три символа, кодируем:
. Делим его на блоки по три символа, кодируем: 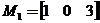 ,
,  . Каждый полученный вектор преобразуем в шифр:
. Каждый полученный вектор преобразуем в шифр: ![]() ,
, ![]() . Передаем по каналу связи C1, C2; злоумышленник, не зная код матричного шифрования, пытается прочесть сообщение, используя, например,
. Передаем по каналу связи C1, C2; злоумышленник, не зная код матричного шифрования, пытается прочесть сообщение, используя, например, 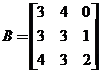 (из достоверных источников ему всё же стал известен определитель матрицы-кода). И получает:
(из достоверных источников ему всё же стал известен определитель матрицы-кода). И получает: ![]() : ничего не вышло, хотя кодировку
: ничего не вышло, хотя кодировку ![]() он все же знает! Тот же, кому адресовано наше сообщение, получив его, дешифрует:
он все же знает! Тот же, кому адресовано наше сообщение, получив его, дешифрует: ![]() ,
, ![]() , и декодирует:
, и декодирует: ![]() .
.
Задание
I. Реализовать приложение для шифрования:
1. Шифруемый текст должен храниться в одном файле, а ключ шифрования (если есть) – в другом.
2. Шифрование производится согласно заданному в варианте алгоритму. Конкретную реализацию алгоритма нужно выбрать самостоятельно. В алфавит шифруемых сообщений, который задан в варианте, нужно добавить символ '_', который является разделителем слов.
3. Зашифрованный текст должен сохраняться в файл.
II. Реализовать приложение для дешифрования:
1. Зашифрованный текст должен храниться в одном файле, ключ (если есть) – в другом.
2. Расшифрованный текст должен сохраняться в файл.
III. С помощью реализованных приложений выполнить следующие задания:
1. Протестировать правильность работы разработанных приложений при различных сообщениях и ключах.
2. Выполнить шифрование нескольких сообщений аналитически (вручную) и сравнить полученные шифротексты с результатами работы шифрующего приложения.
3. Проанализировать шифр на приведённые в лекции типы криптоаналитического вскрытия.
4. Проанализировать шифр с точки зрения совершенной криптостойкости, т. е. проверить выполнение условий теорем (о совершенной криптостойкости симметричной криптосистемы). Ответить на вопрос об идеальной стойкости данного шифра.
5. Сделать выводы о проделанной работе.
Требования к оформлению отчёта
Отчёт должен содержать:
· титульный лист (обязат.);
· задание на лабораторную работу (обязат.);
· описание метода решения заданий;
· описание разработанного программного средства;
· описание проведённых исследований (обязат.);
· программный код, написанный непосредственно студентами (обязат.);
· тестирование программы.
Отчёт не должен содержать орфографических, пунктуационных и смысловых ошибок.
Все его разделы должны быть выдержаны в едином стиле оформления.
Критерии оценивания качества работы
1. Графический интерфейс пользователя:
1 – приложения имеют графический интерфейс пользователя;
0 – приложения имеют интерфейс командной строки;
Л. р. не принимается – иначе.
2. Выполнение требований к оформлению отчёта:
1 – отчёт удовлетворяет всем требованиям;
0 – отчёт не удовлетворяет всем требованиям, но содержит обязательные разделы;
Л. р. не принимается – в отчёте нет хотя бы одного обязательного раздела.
3. Обработка ошибок:
1 – все возможные ошибки и нестандартные ситуации (например, неудачная попытка открытия файла) обрабатываются программой, которая выдаёт соответствующее сообщение;
0 – не все возможные ошибки обрабатываются программой.
4. Применение принципов структурного программирования:
1 – все повторяющиеся либо логически целостные фрагменты программы выделены в качестве функций; работа каждой функции полностью определяется её параметрами (т. е. не используются глобальные переменные, все данные, нужные функции для работы, передаются ей через параметры); программа позволяет без перекомпиляции изменять все параметры, от которых зависит её работа; в тексте программы отсутствуют числовые константы (все необходимые константы объявляются как поименованные);
0 – иначе (не выполняется что-либо из перечисленного).
5. Наличие комментариев в тексте программы:
1 – комментариев достаточно для документирования исходных кодов;
0 – комментариев недостаточно.
6. Глубина понимания материала лабораторной работы каждым членом бригады:
1 – быстрые и правильные ответы на все вопросы;
0 – не на все вопросы ответы правильные и быстрые;
Л. р. не принимается – на половину вопросов ответы неправильные.
Варианты
Вариант | Алгоритм шифрования | Алфавит сообщения | Дополнительная информация |
1 | Шифр Виженера |
| Период |
2 | Шифр Бофора |
| |
3 | Шифр Цезаря |
| |
4 | Видоизмененный шифр Бофора |
| |
5 | Составной шифр Виженера |
| Периоды |
6 | Шифр простой подстановки |
| |
7 | Шифр Вернама |
| |
8 | Диграммная подстановка |
| |
9 | Матричная система |
| (диграммная подстановка) |
10 | Матричная система |
| ( |
11 | Перестановка с периодом |
| Период |
12 | Дробные шифры |
| |
13 | Шифр Виженера |
| Период |
14 | Шифр Бофора |
| |
15 | Шифр Виженера с перемешанным один раз алфавитом |
|
Контрольные вопросы
1. Основные понятия криптографии.
2. Протоколы обмена ключами.
3. Основные аспекты криптоанализа.
4. Общая схема симметричных криптосистем.
5. Математические модели элементарных криптосистем.
6. Криптостойкость симметричных криптосистем.
7. Пессимистическое утверждение Шеннона (теорема).
8. Показатели криптостойкости.
9. Требования, предъявляемые к современным криптографическим системам.
[1] 1 век до н. э. Данный шифр был описан историком . использовал в своей переписке шифр собственного изобретения.


