УДК 519.652

ИВМиМГ СО РАН, Новосибирск

МАТЕМАТИЧЕСКИЙ КОНСТРУКТИВ МЫЛЬНОЙ ПЛЕНКИ В МАСШТАБИРУЕМОМ РЕЛЬЕФЕ

P. A.Kim

Institute of Computational Mathematics and Mathematical Geophysics SB RAS

6, prospect Akademika Lavrentjeva, Novosibirsk, Russian Federation.

THE MATHEMATICAL ABSTRACT OF SOAP FILMS IN THE SCALABLE MODEL OF THE RELIEF

The established relation between the scaled model of the relief developing in laboratory of Processing of images of Institute of Computational Mathematics and mathematical geophysics, allows to use for surface construction of a relief some mathematical ideas, about shapes of soap films and soap bubbles. So they forms constructive elements, and after modification would made generation process more effective.

Классическая минимаксная задача в трехмерном пространстве утверждает, что минимальной поверхностью, заключающей в себе данный объем является сфера. Также было показано[1,2], что поверхностью охватывающей два равных объема является двойной пузырь, полученный сближением сфер таким образом, что плоская поверхность диска, разделяющая объемы и поверхности сфер пересекаются по окружности, под углом 120 градусов (принцип Плато).

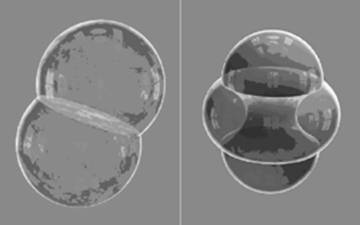
Фиг.1 Варианты строения двойных мыльных пузырей, заключающих в себе два равных объема.

Сложность этой задачи иллюстрируется фиг. 1, где представлены два варианта возможного топологического строения двойного мыльного пузыря. При этом энергетически минимальной оказывается левая конфигурация. Аналогичная задача для кластеров из большего числа пузырей (фиг.2) до настоящего момента не решена. Установленная связь масштабируемой модели рельефа, разрабатываемой в лаборатории Обработки изображений института Вычислительной математики и математической геофизики[3-8], позволяет использовать для построения поверхности рельефа математические идеи, расчета поверхностей мыльных пленок и мыльных пузырей, формируя из них конструктивные элементы, модификацией которых возможно эффективизировать процесс генерации поверхности рельефа.

Фиг.2 Сложный кластер мыльных пузырей

пузырей, заключающих в себе два равных объема.

Представим математические подходы к построению модели мыльной пленки в соответствии с изложением [9]. ведём в пространстве систему координат Oxyz. На фиг.3 изобра­жён контур с натянутой на него плёнкой (т. е. поверхностью) Ω. Пусть проекция Ω на плоскость хОу есть некоторая область на плоскости; обо­значим её через G. Проекцию контура, т. е. границу области G, обозна­чим через Г. Рассмотрим точку (x,y,z) на поверхности Ω и её проекцию, точку (х, у) в области G. Тогда высота точки на поверхности пред­ставляет собой функцию двух переменных: z = и(х, у) или z = и(А), где А — точка с координатами (х, у).

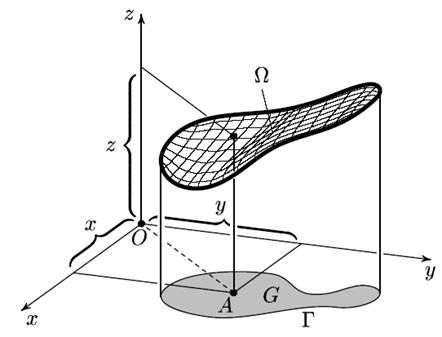
Фиг.3. Математическая модель мыльной пленки

Контур в пространстве задан (известна высота каждой точки кон­тура), значит, дана функция f(Q), Q $ Г. Теперь задача состоит в том, чтобы найти значения функции и(А), А $ G, которая описывает поверхность Ω. Мыльная плёнка, затягивающая замкнутый контур, будет занимать положение, при котором силы натяжения урав­новесятся, что отвечает уравнению Лапласа и имеет следующий вид: (1). Кроме того, для функции и должно выполняться краевое условие u(Q) = f(Q) (2) для всех Q $ Г. Таким образом, требуется найти функцию и(А), А $ G, удовлетво­ряющую уравнению Лапласа (1) и краевому условию (2).

К сожалению, общего метода решения этой задачи не существует, и для его решения предлагается приближённое решение, для чего применяется дискретная мате­матическая модель задачи. Построим на плоскости координатную сетку, раз­бивающую плоскость на маленькие квадратики. Пусть для простоты граница Г области G проходит по сторонам квадратиков. Будем рас­сматривать не все точки G и Г, а только те из них, которые являются узловыми точками сетки (вершинами квадратиков).

.

Фиг.4. Проекция дискретной модели пленки

Пусть Q1, Q2, ..., Qm — узловые точки сетки, лежащие на лома­ной Г, и известны значения f(Qi), 1 M i M m. Теперь задача состоит в том, чтобы найти значения функции и(А) для всех узловых точек А $ G. (Тогда, если сетка достаточно мелкая, по значениям функции и в узлах сетки можно построить хорошее приближение значений этой функции и в остальных точках области G.) Аналогом уравнения Лапласа в дискретном случае будет разностная схема

(3)