§4. Гладкие поверхности. Касательная плоскость и нормаль.
[А] № 000. Показать, что функция  ,
,  является параметрическим представлением эллиптического параболоида
является параметрическим представлением эллиптического параболоида  . Найти его координатную сеть.
. Найти его координатную сеть. Решение. 1) Очевидно, вектор функция  имеет непрерывные частные производные любого порядка. Кроме того ранг матрицы
имеет непрерывные частные производные любого порядка. Кроме того ранг матрицы 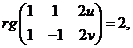 так как
так как  . Следовательно,
. Следовательно,  - гладкая и
- гладкая и  .
.
2) Найдем координатную сеть.
линии  :
:  . Тогда
. Тогда  . Исключив параметр
. Исключив параметр  , получим общие уравнения этой кривой.
, получим общие уравнения этой кривой.  , то есть это параболы.
, то есть это параболы.
линии  :
:  . Тогда
. Тогда  . Исключив параметр
. Исключив параметр , получим общие уравнения этой кривой.
, получим общие уравнения этой кривой.  , то есть это параболы. Нарисуйте картинку! Ÿ
, то есть это параболы. Нарисуйте картинку! Ÿ
[А] № 000. Дана поверхность  . Написать уравнение касательной плоскости, параллельной плоскости
. Написать уравнение касательной плоскости, параллельной плоскости  .
. Решение. 1) Поверхность  . Найдем вектор нормали
. Найдем вектор нормали 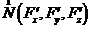 в произвольной фиксированной точке
в произвольной фиксированной точке  :
: . Тогда касательная плоскость имеет уравнение:
. Тогда касательная плоскость имеет уравнение:  .
.
2) Так как касательная плоскость параллельна плоскости  ,
, 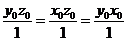 . Так как
. Так как  ,
, 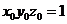 . Решаем систему
. Решаем систему 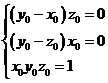
 . Так как
. Так как  ,
, 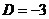 . Итак,
. Итак,  . Ÿ
. Ÿ
[А] № 000. Доказать, что линия 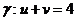 , лежащая на поверхности
, лежащая на поверхности  , является прямой.
, является прямой. Решение. 1) Линия  задана в локальных координатах поверхности. Чтобы доказать, что это прямая, нужно перейти к ее общим уравнениям в координатах
задана в локальных координатах поверхности. Чтобы доказать, что это прямая, нужно перейти к ее общим уравнениям в координатах  .
.
2) Так как  , ее координаты
, ее координаты  удовлетворяют уравнениям, задающим
удовлетворяют уравнениям, задающим  . Получим систему уравнений и исключим из нее параметры
. Получим систему уравнений и исключим из нее параметры  .
. 
 - прямая. Ÿ
- прямая. Ÿ
[А] № 000. Доказать, что все плоскости, касательные к поверхности 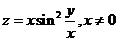 проходят через одну и ту же точку.
проходят через одну и ту же точку. Решение. 1) Найдем вектор нормали  в произвольной фиксированной точке
в произвольной фиксированной точке  и напишем уравнение касательной плоскости в ней.
и напишем уравнение касательной плоскости в ней.
2) 
 .
.
3)  . Вычислим свободный член:
. Вычислим свободный член:  , то есть общая точка
, то есть общая точка  . Ÿ
. Ÿ
Доказать, что все касательные плоскости поверхности  , где
, где  - дифференцируемая функция, проходят через начало координат.
- дифференцируемая функция, проходят через начало координат. Решение. 1) Фиксируем произвольную точку  , принадлежащую поверхности
, принадлежащую поверхности  . Найдем вектор нормали в этой точке:
. Найдем вектор нормали в этой точке: 
 .
.
2) Запишем уравнение касательной плоскости к поверхности  в точке
в точке  :
:  . Вычислим свободный член:
. Вычислим свободный член:  , то есть общая точка
, то есть общая точка  . Ÿ
. Ÿ
Найти множество проекций центра эллипсоида 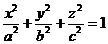 на все его касательные плоскости. Будет ли это множество точек гладкой поверхностью?
на все его касательные плоскости. Будет ли это множество точек гладкой поверхностью? Решение. 1) Найдем вектор нормали  в произвольной фиксированной точке
в произвольной фиксированной точке  и напишем уравнение касательной плоскости в ней.
и напишем уравнение касательной плоскости в ней.  . Тогда уравнение касательной плоскости
. Тогда уравнение касательной плоскости  будет иметь вид:
будет иметь вид: 
 .
.
2) Через точку  проведем прямую
проведем прямую  .
.
3) Искомое множество точек  задается системой
задается системой  , где
, где  - произвольные вещественные числа. Эти числа нужно исключить из системы. Тогда получим уравнение множества
- произвольные вещественные числа. Эти числа нужно исключить из системы. Тогда получим уравнение множества  . Выразим
. Выразим  ,
, 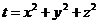 . Подставим в последнее уравнение:
. Подставим в последнее уравнение:  . Тогда
. Тогда  Ÿ
Ÿ
Задачи к зачету и проверочным работам (семинар 4).
Написать уравнения касательных плоскостей и нормалей следующих поверхностей: а)  в точке (3,5,7);
в точке (3,5,7);
б)  в точке
в точке  ;
;
в)  в точке (1,2,2);
в точке (1,2,2);
г)  , параллельных плоскости
, параллельных плоскости  .
.
[Б]№ 000. Доказать, что объем тетраэдра, образованного пересечением координатных плоскостей и касательной плоскости поверхности 
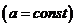 не зависит от выбора точки касания на поверхности. Доказать, что векторное уравнение конической поверхности имеет вид
не зависит от выбора точки касания на поверхности. Доказать, что векторное уравнение конической поверхности имеет вид  , где
, где  - постоянный вектор, задающий вершину конуса,
- постоянный вектор, задающий вершину конуса,  - уравнение направляющей. Найти координатные линии конуса. Написать параметрические уравнения и указать координатную сеть следующих поверхностей: сферы, эллипсоида, однополостного гиперболоида, двуполостного гиперболоида. Написать уравнение касательной плоскости к сфере в произвольной точке и найти на этой сфере множество точек, в которых касательные плоскости параллельны вектору
- уравнение направляющей. Найти координатные линии конуса. Написать параметрические уравнения и указать координатную сеть следующих поверхностей: сферы, эллипсоида, однополостного гиперболоида, двуполостного гиперболоида. Написать уравнение касательной плоскости к сфере в произвольной точке и найти на этой сфере множество точек, в которых касательные плоскости параллельны вектору  . Написать параметрические уравнения тора – поверхности вращения окружности
. Написать параметрические уравнения тора – поверхности вращения окружности  вокруг оси
вокруг оси  . Найти все нормали поверхности
. Найти все нормали поверхности  , проходящие через начало координат. Доказать, что касательные плоскости поверхности
, проходящие через начало координат. Доказать, что касательные плоскости поверхности  отсекают на осях координат отрезки, сумма которых постоянна. Дана поверхность
отсекают на осях координат отрезки, сумма которых постоянна. Дана поверхность  . Доказать, что главная нормаль координатной линии
. Доказать, что главная нормаль координатной линии  в каждой точке является нормалью к поверхности. Доказать, что все касательные плоскости поверхности
в каждой точке является нормалью к поверхности. Доказать, что все касательные плоскости поверхности 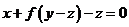 параллельны некоторой прямой (
параллельны некоторой прямой ( - дифференцируемая функция). Доказать, что касательная плоскость к гиперболическому параболоиду пересекает его по двум прямолинейным образующим. Окружность радиуса
- дифференцируемая функция). Доказать, что касательная плоскость к гиперболическому параболоиду пересекает его по двум прямолинейным образующим. Окружность радиуса  перемещается в пространстве так, что ее центр движется по кривой
перемещается в пространстве так, что ее центр движется по кривой  , а плоскость окружности совпадает с нормальной плоскостью кривой. Написать векторное уравнение получающейся трубчатой поверхности и найти координатную сеть на ней. Доказать, что все плоскости, касательные к поверхности
, а плоскость окружности совпадает с нормальной плоскостью кривой. Написать векторное уравнение получающейся трубчатой поверхности и найти координатную сеть на ней. Доказать, что все плоскости, касательные к поверхности  в точках
в точках  принадлежат одному пучку.
принадлежат одному пучку.
![]() имеет непрерывные частные производные любого порядка. Кроме того ранг матрицы
имеет непрерывные частные производные любого порядка. Кроме того ранг матрицы ![]() так как
так как ![]() . Следовательно,
. Следовательно, ![]() - гладкая и
- гладкая и ![]() .
.![]() :
:  . Тогда
. Тогда  . Исключив параметр
. Исключив параметр ![]() , получим общие уравнения этой кривой.
, получим общие уравнения этой кривой.  , то есть это параболы.
, то есть это параболы.![]() :
:  . Тогда
. Тогда  . Исключив параметр
. Исключив параметр![]() , получим общие уравнения этой кривой.
, получим общие уравнения этой кривой.  , то есть это параболы. Нарисуйте картинку! Ÿ
, то есть это параболы. Нарисуйте картинку! Ÿ![]() . Найдем вектор нормали
. Найдем вектор нормали ![]() в произвольной фиксированной точке
в произвольной фиксированной точке ![]() :
:![]() . Тогда касательная плоскость имеет уравнение:
. Тогда касательная плоскость имеет уравнение:  .
. ,
, 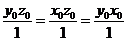 . Так как
. Так как  ,
, 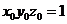 . Решаем систему
. Решаем систему 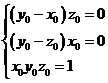
 . Так как
. Так как  ,
, ![]() . Итак,
. Итак,  . Ÿ
. Ÿ![]() задана в локальных координатах поверхности. Чтобы доказать, что это прямая, нужно перейти к ее общим уравнениям в координатах
задана в локальных координатах поверхности. Чтобы доказать, что это прямая, нужно перейти к ее общим уравнениям в координатах ![]() .
.![]() , ее координаты
, ее координаты ![]() удовлетворяют уравнениям, задающим
удовлетворяют уравнениям, задающим ![]() . Получим систему уравнений и исключим из нее параметры
. Получим систему уравнений и исключим из нее параметры ![]() .
. 
 - прямая. Ÿ
- прямая. Ÿ![]() в произвольной фиксированной точке
в произвольной фиксированной точке  и напишем уравнение касательной плоскости в ней.
и напишем уравнение касательной плоскости в ней.
 .
. . Вычислим свободный член:
. Вычислим свободный член: ![]() , то есть общая точка
, то есть общая точка ![]() . Ÿ
. Ÿ![]() , принадлежащую поверхности
, принадлежащую поверхности  . Найдем вектор нормали в этой точке:
. Найдем вектор нормали в этой точке: 
 .
.![]() в точке
в точке  :
:  . Вычислим свободный член:
. Вычислим свободный член:  , то есть общая точка
, то есть общая точка ![]() . Ÿ
. Ÿ![]() в произвольной фиксированной точке
в произвольной фиксированной точке  и напишем уравнение касательной плоскости в ней.
и напишем уравнение касательной плоскости в ней. ![]() . Тогда уравнение касательной плоскости
. Тогда уравнение касательной плоскости  будет иметь вид:
будет иметь вид: ![]()
 .
.![]() проведем прямую
проведем прямую ![]() .
.![]() задается системой
задается системой  , где
, где ![]() - произвольные вещественные числа. Эти числа нужно исключить из системы. Тогда получим уравнение множества
- произвольные вещественные числа. Эти числа нужно исключить из системы. Тогда получим уравнение множества ![]() . Выразим
. Выразим ![]() ,
, ![]() . Подставим в последнее уравнение:
. Подставим в последнее уравнение:  . Тогда
. Тогда ![]() Ÿ
Ÿ![]() в точке (3,5,7);
в точке (3,5,7);![]() в точке
в точке ![]() ;
;![]() в точке (1,2,2);
в точке (1,2,2);![]() , параллельных плоскости
, параллельных плоскости ![]() .
.

