Координация усилий и распространение информации[1]
Константин Сонин, Российская экономическая школа/ЦЭФИР
Ирина Хованская, Лаборатория институционального анализа ГУ-ВШЭ
В работе изучаются стратегические аспекты раскрытия информации в исследовательском коллективе. В некоторых ситуациях дополнительная информация может привести к неэффективному дублированию усилий нескольких исследователей; в этом случае у руководителя лаборатории возникают стимулы к скрытию информации, даже если она помогает увеличить вероятность совершения открытия. Если сотрудники выбирают себе проекты последовательно, желание избежать конкуренции может привести к выбору заведомо менее перспективных направлений исследования.
Введение
Должен ли руководитель исследовательского коллектива предоставлять своим подчиненным информацию? Должен ли быть регулировщик, принудительно раскрывающий информацию конкурентам? Может ли полное раскрытие всей имеющейся информации привести к неэффективности? Выгодно ли руководителю отдавать своим неосведомленным помощникам всю доступную (и существующую) информацию, если ему нужно найти конкретное решение конкретной задачи?
Мы приводим простой пример ситуации, в которой наличие открытой дополнительной информации снижает общественное благо по сравнению с тем случаем, когда агенты полагались только на первоначальную. Типичный пример такой: есть несколько игроков: лаборантов-исследователей, или фирм, состязающихся в «искании клада», одинаково ценного для каждого из участников. Для руководителя и для общества в целом не важно, какой из агентов найдет «клад». Каждый агент должен решить, где он будет искать клад, при том, что объем ресурсов, который можно истратить на исследование, ограничен. Интересен также тот случай, когда агент платит за каждую единицу объема исследований. Если клад расположен на территории, исследуемой одним из агентов, он будет найден. Если клад находят несколько агентов, то они делят его поровну. Если агенты знают, что нахождение клада в каждой точке равновероятно, то области, в которых они будут искать, не будут пересекаться (при условии, что «лес» достаточно большой).
Теперь предположим, что есть руководитель, который получает некоторый сигнал о местонахождении клада. Что будет, если он сообщит эту информацию своим агентам? Области поиска будут пересекаться в том месте, где расположение клада наиболее вероятно. В этом случае возможно, что исследуемая территория будет меньше по сравнению с ситуацией, когда агентам не давали дополнительной информации о местонахождении клада. Следовательно, клад будет найден с меньшей вероятностью.
Хотя R&D литература обширна, примеры одновременных усилий, разработок в одной и той же области обсуждаются не очень часто (см. обзор литературы в Chatterjee, Evans 2004). Проблемы, связанные, как с оптимальным распределением усилий внутри команды, так и с открытием информации, остаются по большей части неисследованными. В то время как конкретные факты про распределение усилий внутри исследовательских лабораторий редко обсуждаются, про внутре-индустриальную конкуренцию известно многое. Chatterjeе, Evans (2004) приводят многочисленные реальные примеры, где одновременные разработки в одной и той же области приводят конкурентов к потере прибыли из-за того, что почти полностью аналогичные изобретения получены и конкурентами. Одними из самых известных примеров являются: гонка Lockheed и Boeing за создание четырех-двигательного турбореактивного cамолета в 50-х годах, соревнование Lockheed и Douglas за создание первого широкофюзеляжного трехдвигательного реактивного авиалайнера в 60-х, параллельные изобретения Casio и Texas Instruments первого электронного микрокалькулятора в 70-х.
Характерная черта нашей модели состоит в том, что конкуренты не обладают никакой личной информацией. В то время как личная информация играет важную роль в работах Hopenhayn, Squintani (2004) и Fershtman, Rubinstein (1997) мы показываем, что результат, в котором благосостояние нарушается из-за поступления новой информации может быть получен и в том случае, когда доступна только общая информация. Общеизвестная информация так же может быть вредной для эффективности, как и личная информация (см., например, Morris, Shin, 2002). К примеру, поток информации тематической литературы может помешать агентам в совершении каких-то социально-выгодных действиях (Banerjee, 1992, Birchandani, Hirshleifer, Welsh, 1992). Мы рассматриваем другой вопрос: обычно агенты получают информацию из поведения других агентов (или своих предшественников), а в нашей модели любое произведенное действие одного из агентов понижает эффективность (и, следовательно, привлекательность) того же действия для других агентов. Те места, которые уже исследуются кем-то, становятся менее привлекательными для остальных агентов. В то же время, в нашей модели нет личной информации, которую можно было бы игнорировать: в нашей модели общая информация понижает общее благо, не принося никакой личной информации агентам. Это на интуитивном уровне противоречит работе Morris, Shin (2002), где, в отсутствии личной информации, более точная общеизвестная информация всегда повышает общественное благо.
Наш первый результат подтверждает результат Bhattacharya, Mookherjee (1986), в работе которых каждая из фирм может участвовать (или неучаствовать) в двух исследовательских проектах (в нашей постановке, проектов бесконечно много). Каждый проект описывается случайной переменной, зависящей от решения фирм. Как и в этой модели, в нашей работе общественные оптимум и некооперативные решения совпадают при максимальной специализации: области поисков агентов в этом случае не пересекаются. Но, в противопоставление Bhattacharya, Mookherjee (1986), неэффективность, связанная с удвоением усилий, не требует отвращения к риску ни со стороны общества, ни со стороны фирм. По аналогичной схеме Dasgupta, Maskin (1987) приходят к выводу что, когда фирмы максимально далеки друг от друга, общественные оптимум может быть достигнут, в то время как слишком большая взаимосвязь приводит к общественной неэффективности. Таким образом, фирмы могут предпочесть более рискованный проект, чем выбрали бы при общественном планировании (см. также Klette, de Meza, 1986). В Fershtman, Rubinstein (1997), два игрока должны найти приз, спрятанный в одной из коробок, но в этой работе, в отличие от нашей, игроки не видят работы друг друга; стратегические аспекты в этом случае совершенно иные.
Работа организована следующим образом. Второй раздел включает постановку задачи, третий раздел состоит из анализа случая, когда соревнующихся двое. В разделе четыре перечисляются некоторые общие результаты и обсуждается устойчивость. Раздел пять заключает работу.
Постановка задачи
Исследуется область – отрезок ![]() . Клад может быть найден в любой точке
. Клад может быть найден в любой точке ![]() с одинаковой вероятностью (то есть распределение вероятности нахождения равномерно на отрезке
с одинаковой вероятностью (то есть распределение вероятности нахождения равномерно на отрезке ![]() ). Зная это, каждый из
). Зная это, каждый из ![]() одинаковых агентов выбирает участок (множество точек)
одинаковых агентов выбирает участок (множество точек)  . Для простоты и без потери общности мы допускаем, что каждое
. Для простоты и без потери общности мы допускаем, что каждое ![]() - это объединение интервалов; соответственно, каждое из множеств
- это объединение интервалов; соответственно, каждое из множеств ![]() измеримо по Лебегу. Обозначим через
измеримо по Лебегу. Обозначим через ![]() Лебегову меру множества
Лебегову меру множества ![]() . Полезность
. Полезность ![]() -ого агента равна
-ого агента равна ![]() , если
, если ![]() , то есть если клад расположен в области, где ищет
, то есть если клад расположен в области, где ищет  -ый агент, в противном случае игрок получает нулевую полезность. Общественное благо (social welfare) равно единице, если клад найден, нулю, если нет: обществу всё равно, кто именно сделал прорыв в исследовании, важен лишь сам факт прорыва, а не личность исследователя.
-ый агент, в противном случае игрок получает нулевую полезность. Общественное благо (social welfare) равно единице, если клад найден, нулю, если нет: обществу всё равно, кто именно сделал прорыв в исследовании, важен лишь сам факт прорыва, а не личность исследователя.
Мы предполагаем, что процесс поиска требует от исследователя некоторых затрат. Мы начнем с рассмотрения пошаговой игры: для ![]() -ого агента
-ого агента ![]() если у поиска есть Лебегова мера
если у поиска есть Лебегова мера ![]() , и
, и ![]() , и
, и ![]() . Обсуждая устойчивость наших теоретических выводов, мы рассматриваем игру с линейной ценой: затраты
. Обсуждая устойчивость наших теоретических выводов, мы рассматриваем игру с линейной ценой: затраты ![]() -ого агента составляют
-ого агента составляют ![]() , где
, где ![]() . Наконец, в завершающей части работы, мы доказываем некоторые результаты для общей функции стоимости
. Наконец, в завершающей части работы, мы доказываем некоторые результаты для общей функции стоимости ![]() .
.
Мы ищем равновесие Нэша, т. е.  -тый агент выбирает область исследований
-тый агент выбирает область исследований![]() , оптимизируя свою полезность и принимая чужой выбор как данность. Сначала мы описываем, что происходит, если ни у кого из игроков нет никакой дополнительной информации; единственная информация, которая используется игроками, это то, что клад расположен с равной вероятностью по имеющейся области. Потом мы переходим к ситуации, в которой агенты обладают некой дополнительной информацией о местоположении клада. Именно, мы предполагаем, что была подкинута монетка с вероятностью выпадения решки, равной
, оптимизируя свою полезность и принимая чужой выбор как данность. Сначала мы описываем, что происходит, если ни у кого из игроков нет никакой дополнительной информации; единственная информация, которая используется игроками, это то, что клад расположен с равной вероятностью по имеющейся области. Потом мы переходим к ситуации, в которой агенты обладают некой дополнительной информацией о местоположении клада. Именно, мы предполагаем, что была подкинута монетка с вероятностью выпадения решки, равной ![]() (настоящее местоположение клада), результаты подбрасывания монеты сообщены агентам. Это даёт игрокам существенную информацию. Если, скажем, выпала решка, условная плотность вероятности нахождения клада в некоторой точке
(настоящее местоположение клада), результаты подбрасывания монеты сообщены агентам. Это даёт игрокам существенную информацию. Если, скажем, выпала решка, условная плотность вероятности нахождения клада в некоторой точке ![]() равна
равна
![]() (*)
(*)
Когда ![]() , мы говорим, что интервал
, мы говорим, что интервал ![]() может быть разделен на конечное число из
может быть разделен на конечное число из ![]() интервалов, исследуемых
интервалов, исследуемых ![]() игроками соответственно. Каждый раз, когда мы используем запись
игроками соответственно. Каждый раз, когда мы используем запись ![]() , мы предполагаем, что
, мы предполагаем, что ![]() . Обозначим через
. Обозначим через ![]() область, исследуемую только игроком
область, исследуемую только игроком ![]() , т. е.
, т. е.![]() .
.
Анализ
Мы начнем с анализа ситуации, в которой участвуют два агента, не имеющие никакой дополнительной информации, за исключением начальной. Если есть нетривиальное пересечение области исследования, то есть![]() , таково, что
, таково, что ![]() , тогда есть непокрытая область
, тогда есть непокрытая область ![]() , полная длина которой не меньше
, полная длина которой не меньше  . Если один из игроков вместо множества
. Если один из игроков вместо множества ![]() будет исследовать область
будет исследовать область ![]() , его полезность увеличится. Из этого немедленно следует, что вероятность нахождения клада равна 1, так как поиски покрывают весь лес. Таким образом мы получаем следующие (почти тривиальные) утверждения:
, его полезность увеличится. Из этого немедленно следует, что вероятность нахождения клада равна 1, так как поиски покрывают весь лес. Таким образом мы получаем следующие (почти тривиальные) утверждения:
Утверждение 1. ![]() любое деление отрезка
любое деление отрезка ![]() , такое, что каждое
, такое, что каждое ![]() имеет длину
имеет длину ![]() и множества
и множества ![]() не пересекаются, является равновесием Нэша. Каждое равновесие Нэша обладает этим свойством.
не пересекаются, является равновесием Нэша. Каждое равновесие Нэша обладает этим свойством.
![]() В равновесии Нэша клад найдется с вероятностью 1. Полезность, поучаемая обществом, соответствует стоимости клада и равна 1.
В равновесии Нэша клад найдется с вероятностью 1. Полезность, поучаемая обществом, соответствует стоимости клада и равна 1.
Так как вероятности выпадения орла и решки равны и все действия агентов симметричны условно на выпадении одного из этих двух значений, мы без ограничения рассматриваем только случай, когда на монетке выпадает орел. В этом случае, ожидаемая полезность каждого игрока от исследования интервала ![]() составляет
составляет

если интервал исследуют оба игрока. Таким образом, полезность равна длине исследуемого интервала ![]() , умноженной на координату его центра. Аналогично заключаем, что выигрыш от исследования интервала одним игроком вдвое больше. Следовательно, имеет смысл переходить от интервала, где действует один игрок
, умноженной на координату его центра. Аналогично заключаем, что выигрыш от исследования интервала одним игроком вдвое больше. Следовательно, имеет смысл переходить от интервала, где действует один игрок  к уже исследованному интервалу
к уже исследованному интервалу ![]() , если центр этого интервала хотя бы вдвое дальше от 0, чем центр первого интервала. Точно также, игрок будет переходить от двойного интервала к неисследуемому интервалу, если выполняется обратное утверждение относительно центров.
, если центр этого интервала хотя бы вдвое дальше от 0, чем центр первого интервала. Точно также, игрок будет переходить от двойного интервала к неисследуемому интервалу, если выполняется обратное утверждение относительно центров.
Любое равновесие по Нэшу в этой игре, ![]() , имеет вид
, имеет вид![]() ,
,  . Естественно, если есть двойной интервал, левее одинарного, занятого первым игроком, тогда второму игроку выгоднее перейти на правый интервал. Значит, профили стратегий
. Естественно, если есть двойной интервал, левее одинарного, занятого первым игроком, тогда второму игроку выгоднее перейти на правый интервал. Значит, профили стратегий ![]() есть равновесие Нэша, если и только если для каждых
есть равновесие Нэша, если и только если для каждых ![]() ,
, ![]() и
и ![]() выполняются описанные ниже условия.
выполняются описанные ниже условия.
Если ![]() , тогда из
, тогда из  следует, что
следует, что ![]() . I
. I ![]()
Действительно, если ![]() , тогда для центров интервалов верно неравенство:
, тогда для центров интервалов верно неравенство: ![]() . Если
. Если ![]() тогда
тогда ![]() -ый игрок получит выгоду от перехода от 1-интервала с центром
-ый игрок получит выгоду от перехода от 1-интервала с центром ![]() к 2-интервалу с центром в
к 2-интервалу с центром в ![]() .
.
Если ![]() , тогда
, тогда  приводит к тому, что
приводит к тому, что ![]() . II
. II ![]()
Действительно,  . Следовательно, если интервал с центром в
. Следовательно, если интервал с центром в ![]() никем не занят, тогда первый игроку выгодно перейти от двойного интервала, с центром в точке
никем не занят, тогда первый игроку выгодно перейти от двойного интервала, с центром в точке ![]() к интервалу с центром в точке
к интервалу с центром в точке ![]() и исследовать его без конкурента.
и исследовать его без конкурента.
Обратно, если профиль стратегий ![]() удовлетворяет двум условиям, то
удовлетворяет двум условиям, то ![]() - равновесие.
- равновесие.
Далее, для любого равновесия  с условием
с условием  ,
, ![]() не может быть меньше
не может быть меньше ![]() . Граница
. Граница ![]() удовлетворяет условию
удовлетворяет условию ![]() , которые приравнивает крайнюю (предельную) полезность исследования дополнительного отрезка слева от
, которые приравнивает крайнюю (предельную) полезность исследования дополнительного отрезка слева от ![]() или двойного интервала. Если
или двойного интервала. Если ![]() , тогда
, тогда ![]() и у нас получается противоречие с условием
и у нас получается противоречие с условием ![]() , когда
, когда ![]() ,
, ![]() и достаточно маленькое
и достаточно маленькое ![]()
Если ![]() , тогда
, тогда 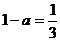 и любое деление отрезка
и любое деление отрезка ![]() на подмножества
на подмножества ![]() и
и ![]() , такие что
, такие что ![]() даёт стратегию
даёт стратегию ![]() с
с ![]() ,
, ![]() и
и  . Очевидно, что такая стратегия удовлетворяет
. Очевидно, что такая стратегия удовлетворяет ![]() и
и ![]() .
.
Если ![]() , тогда
, тогда 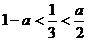 и
и ![]() достаточно мало, существует интервал
достаточно мало, существует интервал ![]() для
для ![]() или 2. Допустим, что
или 2. Допустим, что ![]() . Мы утверждаем, что
. Мы утверждаем, что ![]() . В противном случае существует интервал
. В противном случае существует интервал ![]() , где
, где ![]() . Следовательно,
. Следовательно, ![]() и, согласно
и, согласно ![]() ,
, ![]() , что противоречит условию
, что противоречит условию ![]() .
.
Теперь рассмотрим включение  . Из него следует, что
. Из него следует, что ![]() . Это вытекает из условия
. Это вытекает из условия ![]() для
для ![]() и
и ![]() . Следовательно
. Следовательно
![]() ,
,
где  , и
, и  , где
, где  . Так как,
. Так как,  , мы получаем ограничение снизу на
, мы получаем ограничение снизу на ![]() , а именно
, а именно ![]() или
или ![]() . Таким образом, равновесие (не однозначно) определяется через
. Таким образом, равновесие (не однозначно) определяется через ![]() ,
,  . В частности, из этого следует, что
. В частности, из этого следует, что ![]() .
.
Теперь заметим, что такое ![]() и любого разбиение
и любого разбиение ![]() такое, что
такое, что ![]() и
и ![]() удовлетворяет всем условиям предположения, и, значит, определяет равновесие, описанное в Утверждении 3.
удовлетворяет всем условиям предположения, и, значит, определяет равновесие, описанное в Утверждении 3.
Итак, если информация разглашается, нет равновесий Нэша, в которых агенты исследуют всю площадь - некоторые из поисковых областей обязательно пересекаются. Следовательно, в любом равновесии, клад будет найден с вероятностью, меньшей 1. Конечно, чем больше дважды покрывающиеся исследованием области, тем меньше вероятность нахождения клада.
Следующее утверждение подытоживает вышестоящие рассуждения.
Утверждение 2. Предположим, что игроки получили сигнал вида ![]() (и выпал Орёл). Тогда, любое равновесие по Нэшу имеет вид:
(и выпал Орёл). Тогда, любое равновесие по Нэшу имеет вид: ![]() ,
, ![]() ,
, ![]() , где
, где ![]() , и
, и ![]() это любой кусок интервала
это любой кусок интервала ![]() , такой, что
, такой, что ![]() ,
, ![]() , для такого
, для такого ![]() ,
,  , где достигается равенство только при
, где достигается равенство только при ![]() . В любом подобном равновесии вероятность того, что клад будет найден, равна
. В любом подобном равновесии вероятность того, что клад будет найден, равна ![]() и составляет общественное благо.
и составляет общественное благо.
Стратегическое преимущество
Ранее мы предполагали, что агенты выбирают области, на которых они будут работать, одновременно. На практике это часто не так: может оказаться, что один из игроков делает выбор первым. Если первый игрок может выбрать участок для исследования до того, как это сделает второй, то он может использовать своё первенство, выбирая наиболее выгодное ему равновесие. (Понятно, что любое равновесие в последовательной игре является равновесием в одновременной игре). Как и ранее, мы анализируем ситуацию, когда всем известно, что на монетке выпал Орел.
В соответствии с описанием равновесий из утверждения 3, первый игрок выбирает параметр С, который определяет следующую комбинацию интервалов: двойной интервал: ![]() , и два 1-интервала:
, и два 1-интервала: ![]() и
и  . Таким образом, при данном
. Таким образом, при данном ![]() , максимальная выгода первого игрока равна:
, максимальная выгода первого игрока равна:
 . Наибольшее значение достигается при
. Наибольшее значение достигается при ![]() .
.
Есть два эффекта стратегического преимущества: первый, это уже знакомое нам преимущество первого хода. Первый игрок занимает интервал ![]() . Второй эффект менее очевиден: чтобы избежать соревнования, первый игрок выбирает участок
. Второй эффект менее очевиден: чтобы избежать соревнования, первый игрок выбирает участок ![]() , менее выгодный, чем
, менее выгодный, чем ![]() . В противном случае, первый игрок вынудил бы второго выбрать участок со слишком большим пересечением, чем снизил бы вероятность выигрыша обоих игроков и собственную полезность.
. В противном случае, первый игрок вынудил бы второго выбрать участок со слишком большим пересечением, чем снизил бы вероятность выигрыша обоих игроков и собственную полезность.
Игра с многими агентами
Если агентов ![]() , каждый может исследовать
, каждый может исследовать ![]() интервалы где
интервалы где ![]() и, в зависимости от того, что выпадет на монетке, любой интервал, на котором будет искать менее
и, в зависимости от того, что выпадет на монетке, любой интервал, на котором будет искать менее ![]() игроков, будет лежать левее тех интервалов, где ищут более
игроков, будет лежать левее тех интервалов, где ищут более ![]() игроков. Если
игроков. Если ![]() , то отметим, что
, то отметим, что ![]() и
и ![]() , где
, где ![]() является дополнением
является дополнением ![]() в
в ![]() . Теперь полученные ранее условия можно представить в следующем, более общем виде.
. Теперь полученные ранее условия можно представить в следующем, более общем виде.
Предположение того, что  подразумевает, что
подразумевает, что ![]() или
или
![]()
![]()
Проводя доказательство аналогично доказательству Утверждения 2 для случая, когда ![]() , мы можем вывести следующую теорему.
, мы можем вывести следующую теорему.
Утверждение 3. Совокупность параметров стратегий  ,
, ![]() является равновесием, тогда и только тогда, когда есть точки
является равновесием, тогда и только тогда, когда есть точки 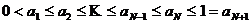 такие, что
такие, что  , где
, где ![]() ,
, 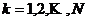 , и, для любых
, и, для любых ![]() ,
, ![]() найдутся
найдутся ![]() и
и ![]() ,
, 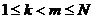 и
и ![]() , следующие условия выполняются
, следующие условия выполняются
![]() если
если  тогда
тогда 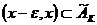 где
где ![]() означает, что
означает, что ![]() для
для ![]() такого, что
такого, что ![]() или
или ![]() .
.
![]() если
если 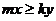 тогда
тогда  ,
,  подразумевает, что
подразумевает, что ![]() такое, что
такое, что ![]() .
.
Это утверждение показывает, что в нашем предположении о структуре информации (а именно, об условной функции распределения вероятности нахождения клада) тройные интервалы и интервалы более высоких порядков невозможны, когда ![]() , то есть
, то есть ![]() , для
, для ![]() . Если
. Если ![]() , тогда условие
, тогда условие ![]() , примененное к
, примененное к ![]() ,
, ![]() , и
, и ![]() ,
,  , и достаточно маленького
, и достаточно маленького ![]() , означает, что
, означает, что
 ,
, 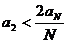 ,
,![]() ,
,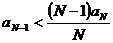 .
.
Объединяя ![]() и
и ![]() , получаем, что
, получаем, что
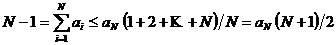 ,
,
Из чего, в свою очередь следует: ![]() . Это невозможно, когда
. Это невозможно, когда ![]() и
и ![]() . Следовательно
. Следовательно ![]() . Аналогично все
. Аналогично все ![]() для
для ![]() .
.
Устойчивость
Может показаться, что основной вывод данной работы (раскрытие существенно-важной информации может ухудшить общественное благо) получен при помощи всяких экзотических допущений. Однако полученный результат устойчив. Вместо конечного количества интервалов, можно рассматривать игру, в которой игрок может исследовать любое измеримое по Лебегу множество. Кроме того, области исследования могут быть не только многомерными, но и бесконечномерными. Можно также рассматривать игру, в которой область исследования каждого игрока не просто ограничена сверху ![]() , а имеет некую стоимость исследования, возрастающую с объемом. Рассмотренная в работе игра является частным случаем этой при ступенчатой функции стоимости: цена исследования области равна 0 будет, если площадь области
, а имеет некую стоимость исследования, возрастающую с объемом. Рассмотренная в работе игра является частным случаем этой при ступенчатой функции стоимости: цена исследования области равна 0 будет, если площадь области ![]() меньше
меньше ![]() и бесконечна, если область имеет больший объем. В более общей постановке, появляется ситуация, в которой даже без дополнительной информации области исследования агентов будут пересекаться, но общественное благо все равно будет убывать с появлением общественной информации с данными ограничениями. Отметим, что сигнал не задан точно (для ясности постановки задачи).
и бесконечна, если область имеет больший объем. В более общей постановке, появляется ситуация, в которой даже без дополнительной информации области исследования агентов будут пересекаться, но общественное благо все равно будет убывать с появлением общественной информации с данными ограничениями. Отметим, что сигнал не задан точно (для ясности постановки задачи).
Отметим, что в случае ступенчатой функции издержек (![]() если
если ![]() , и
, и ![]() если
если ![]() ) равновесие неединственное, область пересечения может изменяться в пределах, описанных в утверждении 1. В случае линейной функции издержек,
) равновесие неединственное, область пересечения может изменяться в пределах, описанных в утверждении 1. В случае линейной функции издержек,  , зона пересечения (а,1] определена однозначно. В этом случае каждый агент сравнивает цену исследования дополнительной зоны,
, зона пересечения (а,1] определена однозначно. В этом случае каждый агент сравнивает цену исследования дополнительной зоны, ![]() , с вероятностью нахождения в ней клада. Для любого
, с вероятностью нахождения в ней клада. Для любого ![]() , определим
, определим  . Теперь рассуждение, приведённое выше, можно привести к следующему, более общему виду. Как и ранее, мы описываем равновесие в случае выпадения Орла. Другой вариант полностью симметричен.
. Теперь рассуждение, приведённое выше, можно привести к следующему, более общему виду. Как и ранее, мы описываем равновесие в случае выпадения Орла. Другой вариант полностью симметричен.
Утверждение 4. Пусть ![]() будет любой функцией распределения вероятностей, и
будет любой функцией распределения вероятностей, и  ,
, ![]() .
.
![]() Существует единственное равновесие Нэша.
Существует единственное равновесие Нэша.
![]() Если
Если ![]() , тогда пересечение областей исследования двух агентов определено, как
, тогда пересечение областей исследования двух агентов определено, как 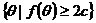 и область
и область  будет исследованной только одним из двух агентов.
будет исследованной только одним из двух агентов.
![]() Для любого
Для любого ![]() ,
,  исследуется
исследуется ![]() агентами
агентами ![]() . Зона
. Зона ![]() исследуется всеми
исследуется всеми ![]() агентами.
агентами.
Как и в случае ступенчатой функции издержек, предположим теперь, что агенты делают свой выбор по очереди, без ограничения на объем выбранной площади. Опять, структура равновесий менее разнообразна, чем в случае ступенчатых издержек. В единственном равновесии первый выбирающий игрок берет ![]() , второй выбирает
, второй выбирает ![]() ,
, ![]() -тый выбирает
-тый выбирает ![]() .
.
Заключение
В этой работе мы строим теорию поиска клада в лесу. Если агенты будут иметь только информацию о том, что клад в лесу есть, вероятность того, что клад будет найден, больше чем, в случае не точного, но информативного публичного сигнала о местонахождении клада. Одно из возможных объяснений состоит в том, что для общей пользы неизвестность важна, тогда как общественная информация заставляет агентов координировать свои действия. Возможным практическим приложением полученных результатов может быть факт, что руководителю (например, R&D contest) бывает стратегически выгодно скрыть некоторую информацию от агентов, которых он посылает за кладом.
Литература
Banerjee, A. (1992) A Simple Model of Herd Behavior // Quarterly Journal of Economics, Vol.107, pp.797-818
Bhattacharya, S., D. Mookherjee, (1986), Portfolio Choice in Research, Development // Rand Journal of Economics, Vol.17, pp.594-605.
Bikhchandani, S., Hirshleifer, D.,, Welch, I.(1992) A Theory of Fads, Fashion, Custom, Cultural Change as Information Cascades// Journal of Political Economy, Vol. 100, pp..
Chatterjee, K., R. Evans (2004) Rivals’ Search for Buried Treasure: Competition, Duplication in R&D // Rond Journal of Economics, Vol 35, No.1, pp.160-183.
Dasgupta, P., Maskin, (1987), The Simple Economics of Research Portfolios // Economic Journal, Vol.87, pp.581-595.
Fershtman, C., *****binstein, (1997) A Simple Model of Equilibrium in Search Procedures // Journal of Economics Theory, Vol.72, No.2,pp.432-441.
Hopehayn, H., F. Squinani (2004) Preemption Games with Private information, mimeo.
Klette, T., D. de Meza, (1986), Is the Market Biased against R&D// Rand Journal of Economics, vol.17, pp.133-139.
Morris, S., Shin, H.S. (2002) Social Value of Pablic Information, mimeo.
Scherer, F. M., (1992) ,International High Technology Competition, // Harvard University Press, Cambridge, Mass.
Welch, I. (1992) Sequential Sales, Learning,, Cascades // Journal of Finance, Vol.47, No.2, pp.695-732.
[1] Авторы выражают глубокую благодарность Изабель Брока, Роджеру Майерсону, Рику Эриксону, Михаилу Островскому, Майклу Риордану, Майклу Шварцу, Пол Сибрайту, Паоло Сиконолфи, Исааку Сонину, Джо Стиглицу, Луиджи Зингалесу и участникам семинара в ЛИА за полезные комментарии, а также Александре Пушкарь за бесценную техническую помощь.


