Стабилизация частоты колебаний автогенераторов

Нестабильность частоты колебаний АГ является одним из наиболее важных показателей автогенераторов. Ее принято выражать в абсолютных и относительных единицах

Наиболее стабильными считаются LC – автогенераторы. Относительная нестабильность таких АГ оценивается величиной . Это примерно на порядок меньше нестабильности частоты АГ других типов.

Различают две основные причины появления нестабильности частоты колебаний АГ: 1) быстротекущие изменения состояния АГ, обусловленные естественными и техническими шумами, 2) медленно текущими изменениями состояния АГ. К медленно текущим процессам относятся старение, изменение окружающей температуры, влажности, давления, изменение нагрузки на автогенератор, уровня питающих напряжений и т. д.

Шумовые процессы приводят к тому, спектральная линия АГ из - функции превращается в случайную функцию времени, и ее принято характеризовать мат. ожиданием, среднеквадратичным отклонением и дисперсией. Среднеквадратичное отклонение частоты от своего мат. ожидания принято именовать кратковременной нестабильностью частоты. Экспериментально она оценивается выборкой измерений за малый промежуток времени (каждый отсчет проводится за время менее одной секунды).

Воздействие медленно текущих процессов оценивается долговременной нестабильностью частоты, которая проявляется в изменении мат. ожидания частоты АГ за большой промежуток времени – минута, час, сутки, год. Следует отметить, что долговременная нестабильность частоты на два - три порядка больше кратковременной нестабильности.

Кратковременная нестабильность частоты АГ является главной причиной фазовых шумов автогенераторов. Долговременная нестабильность приводит к увеличению требуемой ширины канала связи, а также к искажениям передаваемого сообщения при некоторых видах модуляции.

Остановимся на долговременной нестабильности частоты АГ. Поскольку дестабилизирующие воздействия являются медленно текущими процессами, то при анализе долговременной нестабильности АГ можно пренебречь всеми переходными процессами.

Вывод основного уравнения нестабильности АГ

Для краткости в дальнейшем долговременную нестабильность частоты АГ будем именовать просто нестабильностью частоты АГ.

Любое дестабилизирующее воздействие на АГ вызывает изменение одного или нескольких параметров АГ и приводит к нарушению уравнения баланса фаз. Если АГ устойчив, то при измененных параметрах в нем снова устанавливается баланс фаз, но на новой частоте автоколебаний. Это демонстрируется рис.1.

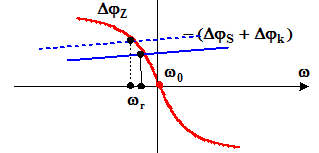
Рис.1.

Припишем исходным параметрам АГ индекс «0» - . Тогда уравнение баланса фаз АГ можно записать в виде

.

Под параметрами АГ следует понимать номинальные значения элементов АГ, напряжений источников питания и смещения, параметров активного элемента АГ, окружающей среды, значения нагрузки на автогенератор, состояние старения, монтажа и т. д. Исходным параметрам АГ соответствует частота генерации , при которой обеспечивается баланс фаз.

Будем полагать, что все параметры независимы. Такое предположение является весьма грубым, но позволяет получить самую простую модель для исследования, и результаты, полученные для такой модели, носят оценочный характер.

Пусть один из параметров АГ изменился под действием дестабилизирующего фактора на величину . Тогда уравнение баланса фаз примет вид

.

Поскольку уравнение записано в неявном виде, то полный дифференциал в частных производных относительно полученных приращений запишется в следующем виде

Зависимости и от частоты в полосе пропускания контура АГ очень слабо выражены, и их производные по частоте можно принять равными нулю. Производная по частоте в окрестности резонансной частоты имеет конечную величину, равную крутизне фазовой характеристики параллельного контура

.

Подставив полученные выше соотношения в уравнение для полного дифференциала, и опустив, для сокращения записи выражения в скобках, получим следующее соотношение для расчета относительного ухода частоты АГ

.

Приняв во внимание независимость параметров АГ, и используя принцип суперпозиции, окончательную формулу для расчета нестабильности частоты АГ можно записать в виде

.

Это выражение принято именовать основным уравнением нестабильности АГ, а коэффициенты - коэффициентами влияния. Коэффициенты влияния чаще всего устанавливаются экспериментально и принимаются каждый со своим знаком.

Из уравнения следует, что чем выше добротность контура и эталонность параметров АГ, тем меньшая величина нестабильность частоты колебаний может быть достигнута.

Параметрическая стабилизация частоты АГ

Под параметрической стабилизацией частоты АГ понимают получение стабильных колебаний путем стабилизации параметров и уменьшение пределов изменения до минимально возможной величины. Если это выполнено относительно всех параметров АГ, то такая параметрическая стабилизация называется полной. Она позволяет получить высокую стабильность частоты колебаний, но очень дорогой ценой. По этой причине всегда прибегают к частичной параметрической стабилизации, которая достигается простыми и относительно дешевыми средствами. К таким средствам относятся выбор элементов АГ с малыми температурным коэффициентом и собственными потерями, стабилизация рабочей точки АГ в установившемся режиме методом трех или четырех резисторов, использование терморезисторов, стабилизация источников питания, стабилизация сопротивления нагрузки на АГ за счет буферного усилителя, жесткий монтаж и ряд других. Это ограничивает минимальную величину нестабильности АГ с частичной параметрической стабилизацией значением 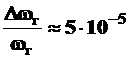.Для получения более высокой стабильности используются другие методы, например, кварцевая стабилизация частоты АГ.

Кварцевая стабилизация частоты АГ с частичной параметрической стабилизацией

Кварцевая стабилизация частоты АГ достигается включением в схему АГ по определенным правилам кварцевого резонатора.

Кварцевый резонатор изготавливается из кварца. Кварц это окись кремния (). В природе он встречается в виде кристаллов двух видов, именуемых α – кварцем и β – кварцем. Первый вид (α – кварц) обладает прямым и обратным пьезоэффектами, второй вид (β – кварц)- пьезоэффектом не обладает. При нагреве α – кварц постепенно теряет свои пьезо свойства и переходит в свою вторую модификацию.

Кварц α-типа встречается в природе в виде кристаллов, представляющих собой почти правильную шестиугольную призму, увенчанную шестигранными пирамидами. Через вершины пирамид и призму проходит оптическая ось «z» (рис.2). Сечение призмы, перпендикулярное оптической оси, имеет вид правильного шестиугольника.

Рис.2.

Перпендикулярно его граням проходят механические оси «y», а через вершины – электрические оси «x». Всего можно провести три механических и три электрических оси. Оптическая ось z вместе с механической осью и соответствующая ей электрическая ось образуют декартовую систему координат.

Для получения кварцевого резонатора из кристалла кварца вырезаются пластинки под определенными углами к осям 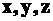. Эти пластинки получили название «срезов» (рис.3).

Рис.3.

Y и X срезы являются простыми и наиболее старыми по времени появления. АТ-срез является сложным и появился значительно позже. Он выполняется под углом к плоскости z-x.

Как и сам α-кристалл пластинки, обладают прямым и обратным пьезоэффектами. Сущность прямого и обратного пьезоэффектов заключается в следующем.

Если в кварцевой пластине имеют место механические колебания, то на ее противоположных поверхностях появляются меняющиеся электрические заряды противоположных знаков.

Если к кварцевой пластине с помощью нанесенных на противоположные стороны проводящих поверхностей подвести переменное электрическое напряжение, то в кварцевой пластине появятся механические колебания, которые, в свою очередь, вызовут появление меняющихся зарядов на ее внешних поверхностях. В замкнутой цепи появляется ток, который называется пьезотоком

.

Величина пьезотока тем больше, чем с большей амплитудой колеблются поверхностные слои кварцевой пластины. Кварцевая пластина становится как бы проводящей. Величина пьезопроводимости определяется соотношением

.

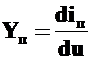Совершенно очевидно, что при максимальная проводимость кварцевой пластины будет появляться, когда противоположные поверхности будут колебаться с максимальной амплитудой и в противоположном направлении. Это условие будет выполняться, если по толщине кварцевой пластины будет укладываться половина длины волны, либо нечетное количество полуволн (рис.4.а, б).

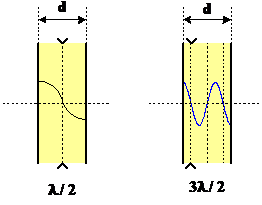
а) б)

Рис.4.а, б.

В первом случае кварцевый резонатор будет работать на основной частоте, а во втором случае - на одной из нечетных гармоник основной частоты (на рис.4 показана 3-я гармоника).

Кроме пьезотока через кварцевый резонатор течет емкостной ток . Он обязан своим появлением емкости , образованной обкладками кварцевой пластины. В качестве диэлектрика выступает кварц. Полный ток, протекающий через пластину кварца и внешнюю замкнутую цепь, запишется в виде

В зависимости от типа среза в кварцевой пластине могут развиваться разные виды механических колебаний: колебания типа сжатие-растяжение, типа сдвига, изгиба, скручивания. Однако только один вид колебания является для данного среза основным. Другие виды колебаний являются побочными. При закреплении кварцевой пластины в корпусе стремятся не вносить затухания в основной вид колебаний, но одновременно внести максимальное затухание в другие побочные виды колебаний, а также в колебания на нерабочих гармониках. На рис.4,а показан способ закрепления кварцевой пластины с колебаниями типа сдвига на основной частоте, а на рис.4,б - на его третьей гармонике. В колебательные процессы типа изгиба и скручивания внесены большие потери выбранным способом закрепления. Закрепление пластины выполняется в специальном корпусе из стекла, пластмассы или металла.

Параметры кварцевого резонатора.

Эквивалентная электрическая схема замещения кварцевого резонатора.

Основную частоту кварцевого резонатора, работающего на механических колебаниях типа сдвига по толщине кварцевой пластины, можно рассчитать по формуле

где d – толщина кварцевой пластины, мм/сек – скорость распространения механических колебаний в кварцевой пластине.

Исходя из механической прочности, толщину d не делают тоньше 0.1 мм. Отсюда максимальное значение основной частоты кварцевых резонаторов не превышает 28 МГц. На более высоких частотах могут работать только гармониковые кварцы. Однако с ростом номера гармоники из-за трения увеличиваются потери в кварцевой пластине. Предельный номер гармоники, которая может быть использована в кварцевом резонаторе, равен одиннадцати. Поэтому максимальная частота гармониковых кварцевых резонаторов не превышает 300 МГц. На более высоких частотах могут использоваться другие резонаторы на основе кварца, например, ПАВ – элементы.

Понятие эталонности кварцевого резонатора.

Под эталонностью понимают способность колебательной системы сохранять неизменными свою резонансную частоту и другие основные параметры. Главным дестабилизирующим фактором является температура и ее изменение. Эталонность кварцевого резонатора будет обеспечиваться, если температурный коэффициент расширения кварцевой пластины близок к нулю.

Простые X и Y срезы обладают относительно большим температурным коэффициентом расширения и, как следствие, большим ТКЧ и низкой эталонностью. Y – срез выполняется путем вырезания пластины из кристалла кварца параллельно плоскости (z-x) и перпендикулярно оси «y». Однако если срез делать под некоторым углом к плоскости (z-x), то ТКР начинает уменьшаться и при углах и становится равным нулю (рис.5).

Рис.5.

Срез под углом получил название АТ-среза, а под углом - ВТ - среза. Оба эти среза сохраняют высокую эталонность при изменении температуры в интервале от до (рис.6)

Рис.6.

Есть срезы, которые хорошо работают при более высоких температурах,

и есть срезы, которые хорошо работают в более низком температурном диапазоне. Кроме того, каждый срез рекомендуется использовать в определенном частотном диапазоне. Например, АТ- срез рекомендован для диапазона частот от 1 до10 МГц, ВТ - срез для диапазона частот менее 1 МГц.

Проводимость кварца и, следовательно, его входное сопротивление кварцевого резонатора зависят от частоты и носят комплексный характер

Характер зависимостей активной и реактивной составляющих входного сопротивления кварцевого резонатора от частоты в окрестности его основной частоты (или гармоники) показан на рис.7, а модуля и фазы входного сопротивления – на рис.6.

Рис.7

Как видно из рисунков, кварцевый резонатор (в дальнейшем просто - кварц) имеет две резонансные частоты, на которых его входное сопротивление чисто активно. Это частота - резонансная частота механических колебаний в кварце, и - резонансная частота электрических колебаний. Характер изменения активной и реактивной составляющих входного сопротивления кварца от частоты позволяет нарисовать электрическую схему замещения кварца, показанную на рис.8.

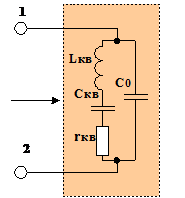
Рис.8.

Изменение активной и реактивной составляющих входного сопротивления такой схемы замещения в диапазоне частот ведет себя также, как входное сопротивление кварцевого резонатора. Замещающие величины имеют следующие значения:

Значения лежат в интервале от десятков мГн до единиц Гн;

Значения составляют сотые – тысячные доли пФ;

Значения , т. е. емкости конденсатора, образованного обкладками резонатора, составляют единицы пФ;

Потери в кварцевом резонаторе имитируются сопротивлением . Значения для генераторных кварцев заключены в интервале от 10 до 100 Ом, а других кварцев – несколько сотен Ом.

Резонансные частоты рассчитываются по формулам

.

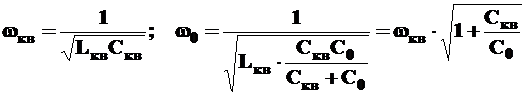Из приведенных формул следует, что резонансные частоты лежат практически рядом на частотной оси и отличаются друг от друга незначительно из-за малости отношения . Это различие составляет от нескольких сотен Гц до единиц кГц.

Характеристическое сопротивление кварца и его добротность определяются отношениями

.

Значения лежат в интервале от 100 кОм до нескольких МОм, а добротность - в интервале от до единиц. Такими значениями добротности не обладает ни какая другая колебательная система. Все это говорит об уникальности кварцевых резонаторов.

Из рис.6 видно, что входное сопротивление кварца на большом частотном участке носит емкостный характер и только в узком интервале частот, заключенном между ][ носит индуктивный характер. При чем крутизна зависимостей и в окрестности частоты последовательного резонанса очень велика. Эти особенности лежат в основе применения кварцев для стабилизации частоты АГ.

Способы включения кварцевых резонаторов в схемы АГ

Для стабилизации частоты колебаний АГ кварцевые резонаторы можно включать тремя способами.

При первом способе кварц включается вместо одной из индуктивностей трехточечной схемы АГ. На рис. 9 кварц включен вместо индуктивности L3 АГ, выполненного по схеме емкостной трехточки.

Рис.9.

В индуктивной трехточке АГ кварц может заменить любую из индуктивностей контура. Чаще всего им заменяют индуктивность L2, которая включается между коллектором и эмиттером. В этом случае шунтирующее действие проводимости транзистора Y22 кварцевого резонатора минимально. Кварц во всех перечисленных схемах выполняет роль частотно зависимой индуктивности с крутизной, пропорциональной добротности кварцевого резонатора.

Если пренебречь инерционностью носителей заряда транзистора и потерями элементов контура АГ, то частоту генерации применительно к схеме рис.9 можно найти из уравнения

; или

Графическое решение этого уравнения показано на рис.10.

Рис.10.

Как видно из рис.10, частота генерации лежит в интервале ][ и незначительно превышает .

Схемы АГ, в которых кварц замещает одну из индуктивностей контура, получили название осцилляторных схем АГ. На рис.11 представлена рабочая схема АГ с кварцевой стабилизацией.

Рис.11.

При втором способе включения кварца в схему АГ его помещаю в разрыв цепи обратной связи, так как это показано на рис.12.

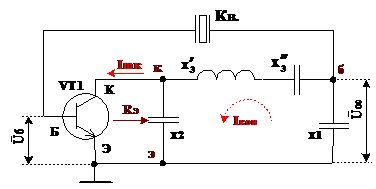
Рис.12.

В этой схеме кварц совместно с входным сопротивлением транзистора образует частотно зависимый делитель. На частоте последовательного резонанса кварца обеспечивается максимальное значение модуля коэффициента передачи от контура к базе транзистора. Баланс фаз для такой схемы АГ принимает вид

.

Благодаря большой крутизны фазовой характеристики кварца в окрестности последовательного резонанса, баланс фаз выполняется только на частоте последовательного резонанса или в непосредственной близости от него. Таким образом, за частоту генерации следует принять . На рис.13 представлена рабочая схема АГ с кварцем в цепи обратной связи.

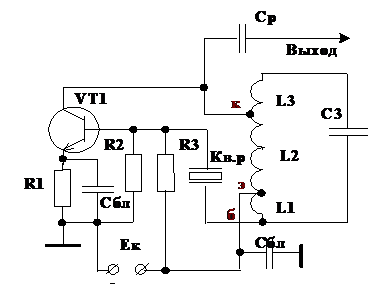
Рис.13.

Третий способ включения кварца в схему АГ основан на принципе затягивания частоты генерации АГ колебательным процессом, который развивается в колебательной системе с кварцевым резонатором, связанным контуром АГ. Такой способ стабилизации частоты АГ используется редко, т. к. связан с полосой захвата частоты АГ внешним воздействием. Подробнее с этим способом можно познакомиться в [(Баскаков)].