1.5. Движение заряженных частиц в электрическом поле
1.5.1. Электрон, обладающий нулевой начальной скоростью, попадает в однородное электрическое поле напряжённостью Е = 200 кВ/м. Какое расстояние пролетит, предоставленный самому себе электрон за время t = 1 нс? Какой скорости он достигнет?
Решение
1. Определим величину силы Кулона, действующую на электрон массой m @ 1×10 -30 кг при попадании его в электрическое поле напряжённостью Е
![]() , (1)
, (1)
где е @ 1,6×10 -19 Кл - заряд электрона.
2. Для электрона, который в рамках классических представлений считается частицей, справедлив второй закон Ньютона, посредствам которого можно найти ускорение частицы
![]() . (2)
. (2)
Впечатляющая величина ускорения обусловлена весьма малой массой электрона и относительно большим значением силы.
3. Путь, пройденный электроном за заданный промежуток времени найдём, используя кинематические соотношения
![]() . (3)
. (3)
4. Скорость электрона в конце заданного промежутка времени определим из закона сохранения импульса
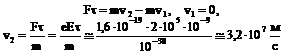 . (4)
. (4)
1.5.2. Протон и электрон необходимо разогнать до скорости v = 30 Мм/с. Какую разность потенциалов они должны при этом пройти?
Решение
1. Работа по перемещению в электрическом поле заряда в соответствии с теоремой об изменении кинетической энергии равна
![]() , (1)
, (1)
где v1 и v2 - начальная и конечная скорость частицы, m - масса частицы. Если предположить, что разгон частиц начинается из состояния покоя, то уравнение (1) можно упростить
![]() . (1)
. (1)
2. Разность потенциалов, необходимая для разгона электрона, обладающего массой me @кг и зарядом е @ 1,6×10 -19 кг
![]() . (2)
. (2)
3. Разность потенциалов, необходимая для разгона до заданной скорости протона, имеющего массу mp @ 1,67×1кг и заряд p @ 1,6×1Кл
![]() . (3)
. (3)
1.5.3. Между катодом и анодом разность потенциалов составляет U = 90 В, расстояние равно r = 1×10 - 3 м. С каким ускорением а движется от катода к аноду электрон? За какое время он проходит расстояние r. Какова скорость электрона v в момент удара о поверхность анода? За какое время t электрон пролетает расстояние от катода до анода?
Решение
1. Воспользовавшись уравнением (1) предыдущей задачи, определим конечную скорость электрона перед ударом в анод
![]() , (1)
, (1)
2. Запишем кинематические уравнения движения электрона и определим время полёта электрона от катода к аноду
 . (2)
. (2)
3. Ускорение электрона определим из верхнего уравнения системы уравнений (2)
![]() . (3)
. (3)
1.5.4. Пылинка массой m = 1×10 - 12 кг, несущая на себе электрический заряд в пять электронов, прошла в вакууме ускоряющую разность потенциалов U = 3 10 6 В. Какова скорость и кинетическая энергия пылинки?
Решение
1. Изменение энергии пылинки, в соответствии с теоремой об изменении кинетической энергии равно работе сил электрического поля
![]() . (1)
. (1)
2. Выразим энергию пылинки в электрон-вольтах
![]() . (2)
. (2)
3. Определим скорость пылинки
![]() . (3)
. (3)
1.5.5. Заряженная частица, пройдя ускоряющую разность потенциалов U = 0,6 МВ, приобрела скорость v = 5,4 Мм/с. Определить удельный заряд частицы (отношение заряда к массе).
Решение
1. Запишем теорему об изменении кинетической энергии частицы и определим удельный заряд
![]() . (1)
. (1)
1.5.6. Протон, начальная скорость которого была равна v0 = 100 км/с, пройдя ускоряющее электрическое поле с напряжённостью Е = 300 В/см удвоил свою скорость. Какой путь прошёл протон, если вектор его скорости совпадал по направлению с вектором напряжённости?
Решение
1. Определим величину силы Кулона, действующей на протон, обладающий массой m = 1,67×1кг и зарядом е = +1,6 -19 Кл
![]() . (1)
. (1)
2. Запишем теорему об изменении кинетической энергии протона при прохождении им электрического поля
![]() , (2)
, (2)
и определим, пройденный протоном путь s
![]() . (3)
. (3)
1.5.7. Бесконечная плоскость заряжена отрицательно с поверхностной плотностью s = 35,4 нКл/м2. В направлении силовой линии поля, созданного плоскостью движется электрон. На расстоянии y0 = 5×10 - 2 м электрон имел кинетическую энергию К = 80 эВ. На какое минимальное расстояние ymin электрон может приблизиться к плоскости?
Решение
1. Напряжённость электрического поля плоскости
![]() . (1)
. (1)
2. Тормозная сила, действующая со стороны электрического поля на электрон
![]() . (2)
. (2)
3. Электрон остановит своё движение в момент времени, когда работа кулоновской силы, тормозящей его движение, станет равной по величине начальной кинетической энергии, электрон, при этом пройдёт некоторое расстояние y
![]() , (3)
, (3)
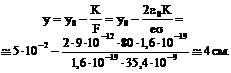 (4)
(4)
4. Расстояние до пластины в момент остановки электрона определится как
![]() . (5)
. (5)
1.5.8. Электрон, летевший горизонтально со скоростью v0 = 1,6 Мм/с, влетел в однородное электрическое поле с напряжённостью Е = 90 В/см, направленное вертикально. Определить вектор скорости электрона v через t = 1 нс?
|
Решение
1. В вертикальном электрическом поле на электрон будет действовать сила Кулона, которая обеспечивает ускорение, направленное по оси оy
![]() , (1)
, (1)
где е @ 1,6×1Кл - заряд электрона, m @ 1×1кг - масса электрона.
2. Поскольку проекция ускорения на ось ох равна нулю, то горизонтальное движение электрона будет протекать с начальной скоростью v0, т. е. vx = v0, а вертикальная составляющая скорости будет определяться уравнением
![]() (2)
(2)
в рассматриваемом случае, с учётом уравнения (1):
![]() . (3)
. (3)
3. Таким образом, через время t модуль скорости электрона будет равен
![]() . (4)
. (4)
4. Определим далее угол a между осью ох и вектором скорости в заданной точке траектории
![]() . (5)
. (5)
|
1.5.9. В плоский конденсатор влетает электрон со скоростью v0 = 2 Мм/с, направленной перпендикулярно вектору напряжённости электрического поля. На какое расстояние h сместится электрон к нижней обкладке конденсатора за время пролёта пластин конденсатора? Длина пластин составляет х = 5 см, расстояние между пластинами d = 2 см, разность потенциалов между обкладками U = 2 В.
Решение
1. Запишем кинематические уравнения движения электрона под действием постоянной силы Кулона F = eE= eU/d
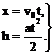 (1)
(1)
2. Поскольку вдоль горизонтальной оси движение электрона происходит с постоянной скоростью, то время пролёта конденсатора можно определить как
![]() . (2)
. (2)
3. Смещение электрона по вертикали, таким образом, можно представить следующим уравнением
![]() . (3)
. (3)
4. Вертикальное ускорение электрона а определится посредствам второго закона Ньютона
![]() . (4)
. (4)
5. Подставим значение ускорения из уравнения (4) в уравнение (3)
![]() . (5)
. (5)
1.5.10. Протон и a - частица из состояния покоя проходят ускоряющее электрическое поле. В каком отношении будут находиться их скорости?
Решение
1. Как известно, a - частица состоит из двух протонов и двух нейтронов, поэтому заряд a - частицы в два раза больше заряда протона, т. е. qa = 2qp, а масса - в четыре раза больше, т. е. ma = 4 mp.
2. При прохождении частицами одинаковой разности потенциалов Dj силами поля будет совершаться работа и они будут приобретать соответствующую кинетическую энергию
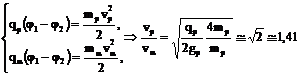 . (1)
. (1)
1.6. Электрический диполь. Свойства диэлектриков
|
1.6.1. Вычислить электрический момент диполя p, если его заряд равен q = 10 нКл, плечо l = 0,5 см.
Решение
1. Электрический момент диполя определяется в виде скалярного произведения модуля заряда диполя, на плечо
![]() . (1)
. (1)
|
1.6.2. Диполь c электрическим моментом р = 0,12 нКл×м образован двумя точечными зарядами q. Определить напряжённость электрического поя Е и потенциал j в точках А и В, находящихся на расстоянии r = 8 см от центра диполя.
Решение
1. Определим напряжённость электрического поля диполя в точка А, которая отстоит от центра диполя на расстоянии r = 0,08 м, причём радиус-вектор r составляет с осью диполя угол a = p/2, т. е. cosa = 0
![]() . (1)
. (1)
2. Потенциал в точке А
![]() . (2)
. (2)
3. Напряжённость поля диполя в точке В
 .(3)
.(3)
4. Потенциал поля диполя в точке В
![]() . (4)
. (4)
1.6.3. Определить напряжённость Е и потенциал j электрического диполя с моментом р = 4 пКл×м на расстоянии r = 0.1 м от центра диполя в направлении a = 600 с вектором электрического момента.
|
Решение
1. Напряжённость электрического поля в точке А определится уравнением
![]() , (1)
, (1)
 2. Потенциал диполя в заданной точке
2. Потенциал диполя в заданной точке
![]() . (2)
. (2)
1.6.4. Диполь с электрическим моментом р = 1 пКл×м равномерно вращается с частотой n = 10 3 с - 1 относительно оси, проходящей через центр диполя перпендикулярно своему плечу. Получить закон изменения потенциала во времени для некой точки, отстоящей от центра диполя на расстоянии r = 1 см и лежащей в плоскости диполя. В начальный момент времени потенциал равен нулю j(0) = 0.
|
Решение
1. В данном случае вектор электрического момента, оставаясь постоянным по модулю, изменяет во времени своё положение, другими словами, величина угла a = f(t). Эти обстоятельства приводят к тому, что величина потенциала тоже станет зависимой от времени
![]() . (1)
. (1)
2. Определим амплитудное значение потенциала, которое будет иметь место при t = 0, когда cos(2pn0) = 1
![]() . (2)
. (2)
3. Определим далее циклическую частоту вращения р
![]() , (3)
, (3)
и запишем уравнение потенциала, как функцию времени
![]() . (4)
. (4)
Таким образом потенциал в точке А, расположенной в плоскости вращения диполя изменяется во времени по закону косинуса.
1.6.5. Электрический диполь с моментом р = 0,1 нКл×м укреплён на упругой нити. Когда в пространстве, где находится диполь, было создано электрическое поле напряжённостью Е = 3 кВ/м перпендикулярное вектору момента, диполь повернулся на угол a = 300. Определить постоянную кручения нити z, равную моменту закручивающей силы, отнесённому к 1 рад.
|
Решение
1. Определим механический момент пары сил, возникающий вследствие действия сил Кулона, приложенных к каждому из зарядов, составляющих диполь
![]() (1)
(1)
2. Постоянная кручения, как отмечено в условии задачи представляет собой механический момент действующей пары сил, отнесённый у углу закручивания, выраженному в радианах
![]() . (2)
. (2)
|
1.6.6. Перпендикулярно плечу диполя с электрическим моментом р = 12 пКл×м возбуждено однородное электрическое поле напряжённостью Е = 300 кВ/м. Под действием поля диполь начинает поворачиваться относительно оси, проходящей через его центр. Определить угловую скорость диполя w в момент прохождения им положения равновесия. Момент инерции диполя относительно оси, перпендикулярной плечу и проходящей через центр диполя равен J = 2×10 - 9 кг×м2.
Решение
1. Кинетическая энергия вращательного движения определяется как
![]() . (1)
. (1)
2. Механический момент, действующий на диполь в электрическом поле, равен
![]() . (2)
. (2)
3.Полная работа при повороте диполя в электрическом поле зависит от электрического момента и угла поворота
![]() . (3)
. (3)
4. При прохождении состояния равновесия a1 =0, a2 = p/2, т. к. электрическое поле в начальном положении диполя перпендикулярно его оси
![]() . (4)
. (4)
1.6.7. Колба проекционной лампы заполненная криптоном, находящимся под давлением р = 20 МПа при температуре Т = 400 К помещена в электрическое поле напряжённостью Е = 2 МВ/м. Найти диэлектрическую проницаемость криптона и его поляризованность Р. Поляризуемость криптона принять равной a = 4,5×10 - 29 м3.
Решение
1. Диэлектрическая проницаемость e входит в уравнение Клаузиуса - Мосотти
![]() , (1)
, (1)
где n - концентрация атомов криптона.
2. Концентрацию молекул газа определим из уравнения молекулярно-кинетической теории
![]() , (2)
, (2)
где kB = 1,4×1Дж/К - постоянная Больцмана.
3. Подставим значение n из уравнения (2) в уравнение (1)
![]() . (3)
. (3)
4. Разрешим уравнение (3) относительно величины диэлектрической проницаемости e
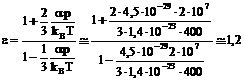 . (3)
. (3)
5. Величина поляризованности определяется в общем виде уравнением
![]() , (4)
, (4)
где рi - дипольный момент, наведённый в i - м атоме, k - число атомов в объёме DV. При нахождении атомов в однородном электрическом поле все атомы имеют дипольные моменты, совпадающие по направлению и по величине, это даёт возможность от геометрического сложения в уравнении (4) перейти к алгебраическому
![]() . (5)
. (5)
6. С другой стороны, отношение полного числа атомов к занимаемому ими объёму равно концентрации k/DV = n
![]() . (6)
. (6)
7. Выразим далее дипольный момент через поляризуемость a и напряжённость локального электрического поля Е*
![]() . (7)
. (7)
8. Выразим напряжённость локального поля Е* через напряжённость внешнего поля Е, а концентрацию через давление и температуру
 (8)
(8)
1.6.8. В близи атома на расстоянии r = 1 нм находится a - частица, представляющая собой дважды ионизированный атом гелия с зарядом 2|e|. Электрическое поле a - частицы индуцирует электрический момент атома р = 1×10 - 32 Кл×м. Найти поляризуемость этого атома.
Решение
1. Поляризуемость a пропорциональна индуцированному электрическому моменту р и обратно пропорциональна напряжённости локального магнитного поля
![]() . (1)
. (1)
2. В данном случае внешнее электрическое поле создаётся a - частицей, оно же, по сути, будет являться и локальным
![]() . (2)
. (2)
3. Совместим уравнения (1) и (2)
![]() . (3)
. (3)
1.6.9. Вода имеет плотность r = 103 кг/м3 и показатель преломления n = 1,33. Определить электронную Поляризуемость aе молекул воды.
Решение
1. Электронная поляризуемость молекул определяется формулой Лоренц - Лорентца
![]() , (1)
, (1)
где m = 18×10 - 3 кг/моль, NA = 6×1023 моль - 1.
2. Разрешим уравнение (1) относительно aе
![]() . (2)
. (2)
![]() . (3)
. (3)
1.7. Электрическая ёмкость. Конденсаторы
1.7.1. Определить электрическую ёмкость С уединённого проводящего шара радиусом R = 1 м, погруженного в трансформаторное масло.
Решение
1. Диэлектрическая проницаемость керосина e = 2, ёмкость шара определяется уравнением
![]() . (1)
. (1)
1.7.2. Найти электрическую ёмкость С проводящей сферы, погруженной в воду. Радиус сферы составляет R = 2 см.
Решение
1. Воспользуемся уравнением предыдущей задачи, с учётом значения диэлектрической проницаемости воды e =80
![]() . (1)
. (1)
1.7.3. Определить электрическую ёмкость Земли, приняв её за шар радиусом R @ 6,4×105 м.
Решение
1. Воспользуемся уравнением для электроёмкости шара
![]() . (1)
. (1)
1.7.4. Два металлических шара радиусами R1 = 2 см и R2 = 6 см соединяют проводником с пренебрежимо малой ёмкостью и сообщают электрический заряд Q = 1 нКл. Определить поверхностную плотность зарядов.
Решение
1. Запишем уравнения электрической ёмкости шаров
![]() . (1)
. (1)
2. Электрическая ёмкость шара определяется, как известно, величиной размещённого на нём заряда и потенциалом C = Q/j. Поскольку шары соединили безъемкостным проводником, то потенциал обоих шаров будет одинаков, а вот электрические ёмкости - разные
![]() , (2)
, (2)
где Q1, Q2 и С1, С2 - заряды и электроёмкости шаров, соответственно.
3. В соответствии с законом сохранения заряда
![]() . (3)
. (3)
4. Образуем систему уравнений, из которой можно найти заряд каждого шара
 , (4)
, (4)
![]() , (5)
, (5)
![]() , (6)
, (6)
![]() . (7)
. (7)
5. Определим далее поверхностную плотность зарядов
 , (8)
, (8)
![]() . (9)
. (9)
1.7.5. Шар радиусом R1 = 6 см заряжен до потенциала j1 = 300 В, а шар радиусом R2 = 4 см до потенциала 500 В. Найти потенциал шаров после их соединения безъемкостным проводником.
Решение
1. Запишем уравнения, определяющие электрическую ёмкость шаров
![]() . (1)
. (1)
2. Общая ёмкость шаров после соединения
![]() . (2)
. (2)
3. Поскольку известны потенциалы шаров до их соединения, можно определить их заряды
![]() . (3)
. (3)
4. Электрический заряд шаров после их соединения безъёмкостным проводником
![]() . (4)
. (4)
5. Потенциал шаров после их соединения
![]() . (5)
. (5)
1.7.6. Медное пушечное ядро, массой m = 10 кг вследствие трения при полёте о воздух приобрело электрический заряд, эквивалентный N = 1010 некомпенсированным элементарным зарядам. Определить электрическую ёмкость ядра и его потенциал.
Решение
1. Для определения электрической ёмкости пушечного ядра сферической формы необходимо знать его радиус, который можно найти по известной массе m и плотности меди r = 8,9×103 кг/м3
![]() . (1)
. (1)
2. Электрическая ёмкость медного пушечного ядра
![]() . (2)
. (2)
3. Электрический потенциал ядра
![]() . (3)
. (3)
1.7.7. Заряженное проводящее тело сферической формы радиусом R = 2 см обладает электрической энергией W = 1 Дж. Определить потенциал этого тела.
Решение
1. Электрическая энергия и потенциал заряженного тела связаны следующим уравнением
![]() . (1)
. (1)
1.7.8. Найти электрическую ёмкость С плоского конденсатора с площадью пластин s = 100 см2 и расстоянием между ними d = 0,1 мм заполненным слюдой с диэлектрической проницаемостью e = 7.
Решение
1. Электрическая ёмкость плоского конденсатора определяется уравнением
![]() . (1)
. (1)
|
1.7.9. Между пластинами плоского конденсатора, заряженного до разности потенциалов U = 600 В, находятся два слоя диэлектриков: стекло толщиной d1 = 7 мм и эбонит толщиной d2 = 3 мм. Площадь каждой из пластин s = 200 см2. Определить электрическую ёмкость конденсатора С, смещение D, напряжённость Е и падение потенциала на каждом слое диэлектрика.
Решение
1. Примем диэлектрическую проницаемость стекла e1 = 7, проницаемость эбонита e2 = 3. Предложенную в задаче конструкцию можно рассматривать как два последовательно соединённых конденсатора, причём
![]() , (1)
, (1)
 , (2)
, (2)
![]() . (3)
. (3)
2. Определим заряд конденсатора
![]() . (4)
. (4)
3. Поверхностная плотность электрического заряда s, которая по величине совпадает со значением смещения D
![]() . (5)
. (5)
4. Поскольку С1 = С2 = 180 пФ, то j1 = j2 = 300 В, а для напряжённости поля Е можно записать следующие соотношения
![]() . (6)
. (6)
![]() . (7)
. (7)
1.7.10. Расстояние между пластинами плоского конденсатора d = 1,3 мм, площадь пластин составляет s = 20 см2. В пространстве между пластинами конденсатора расположены два слоя диэлектриков: слюда толщиной d1 = 0,7 мм и эбонита толщиной d2 = 0,3 мм. Определить электрическую ёмкость такого конденсатора.
|
Решение
1. Данную конструкцию электрической ёмкости можно рассматривать как три последовательно включённых конденсатора: один с диэлектриком из слюды, второй - из эбонита, третий с диэлектриком из воздуха.
2. Диэлектрическая проницаемость слюды e1 = 7, диэлектрическая проницаемость эбонита e2 = 3, диэлектрическая проницаемость воздуха e3 = 1.
3. Три последовательно соединённых конденсатора имеют общую ёмкость, определяемую уравнением
![]() . (1)
. (1)
4. Ёмкости отдельных конденсаторов соответственно равны
![]() ,
, ![]() ,
, ![]() , (2)
, (2)
5. Сопоставим уравнения (1) и (2)
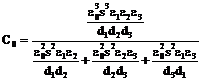 . (3)
. (3)
6. Преобразуем последнее уравнение к более простому виду
 , (4)
, (4)
![]() , (5)
, (5)
![]() . (6)
. (6)
7. Поделим числитель и знаменатель уравнения (6) па произведение диэлектрических проницаемостей (e1e2e3)
 , (7)
, (7)
![]() , (8)
, (8)
8. Подставим в уравнение (8) заданные по условию задачи и справочные данные
![]() . (9)
. (9)
1.7.11. На пластинах плоского конденсатора равномерно распределён электрический заряд плотностью s = 0,2 мкКл/м2. Расстояние между пластинами d = 1 мм. На сколько изменится разность потенциалов на обкладках конденсатора, если расстояние между пластинами увеличить в три раза.
Решение
1. Разность потенциалов на обкладках конденсатора и его заряд связаны следующим соотношением
![]() . (1)
. (1)
2. При увеличении расстояния между обкладками изменяется ёмкость конденсатора и разность потенциалов между обкладками, другими словами
![]() . (2)
. (2)
3. Определим разность потенциалов при измени расстояния между обкладками
![]() . (3)
. (3)
|
1.7.12. Два кубика электрической ёмкостью С1 и С2 заряжены до потенциалов j1 и j2 соответственно. Определить ёмкость прямоугольной призмы, составленной из этих кубиков.
Решение
1. Поскольку соединяемые тела не представляют собой конденсаторы в классическом их понимании, то использовать для нахождения общей ёмкости формул последовательного или параллельного соединения не представляется возможным. В данном случае применимы законы сохранения заряда и энергии.
2. Запишем законы сохранения заряда и энергии
 . (1)
. (1)
3. Перепишем систему уравнений (1) с учётом значений зарядов кубиков и общей их энергии Wo
 . (2)
. (2)
4. Совместим уравнения системы (2)
![]() , (3)
, (3)
откуда
![]() . (4)
. (4)
1.7.13. На плоский конденсатор с парафиновым диэлектриком (e = 2) подано напряжение U = 4000 В. Расстояние между обкладками d = 2 мм. Определить поверхностную плотность зарядов s на обкладках.
Решение
1. Выразим электрическую ёмкость конденсатора через его электрические и геометрические параметры
![]() , (1)
, (1)
2. Подставим в уравнение (1) заданные величины
![]() . (2)
. (2)
|
1.7.14. Плоский конденсатор представляет собой две круглые проводящие пластины радиусом r = 1 см, пространство между которыми заполнено винипластом с диэлектрической проницаемостью e = 3. Какой максимальный заряд Qmax должен быть на пластинах, чтобы при напряжённости электрического поля Е = 45 кВ/мм произошёл электрический пробой диэлектрика?
Решение
1. Для решения задачи воспользуемся уравнением (1) предыдущей задачи
![]() . (3)
. (3)
2. Разрешим уравнение (3) относительно заряда Q
![]() . (4)
. (4)
|
1.7.14. Электростатические весы представляют собой устройство, в котором действие силы тяжести компенсируется силой притяжения между разноимённо заряженными пластинами, расположенными на расстоянии d = 1 мм. Какой добавочный груз нужно поместить на чашку весов, чтобы расстояние между пластинами сохранилось при зарядке конденсатора напряжением U = 1 кВ? Площадь пластин составляет s = 5×10 - 3 м2.
Решение
1. Определим силу Кулона, действующую на положительно заряженную пластину
![]() . (1)
. (1)
2. С другой стороны, заряд конденсатора можно выразить через его ёмкость и разность потенциалов между обкладками
![]() . (2)
. (2)
3. Подставим значение заряда из уравнения (2) в уравнение (1)
![]() . (3)
. (3)
4. Определим массу перегрузка m для уравновешивания весов
![]() . (4)
. (4)
|
1.7.15. Электростатические весы устроены так, что одна из пластин конденсатора укреплена неподвижно, а вторая соединена с пружиной с коэффициентом жёсткости k. Площадь обкладок конденсатора равна s. Определить удлинение пружиныDl при сообщении пластинам равных по модулю и противоположных по знаку зарядов Q.
Решение
1. Воспользовавшись уравнением (1) предыдущей задачи, определим величину силы, возникающей при взаимодействии разноимённо заряженных пластин
![]() . (1)
. (1)
2. Притяжение пластин будет сопровождаться удлинением пружины на величину Dl и возникновением силы упругости Fу = k×Dl, другими словами
![]() . (2)
. (2)
|
1.7.16. В плоском переменном конденсаторе ёмкость изменяется путём увеличения расстояния между пластинами. Какую работу совершает источник тока, к которому подключены пластины, если ёмкость меняется от С1 до С2, а заряд конденсатора остаётся равным Q?
Решение
1. Как было показано в предыдущих задачах, разноимённо заряженные пластины притягиваются с силой
![]() . (1)
. (1)
2. При элементарном изменении расстояния между пластинами на dу ёмкость конденсатора изменяется на dC, при этом внешним источником энергии, каковым является батарея, совершается элементарная работа
![]() , (2)
, (2)
полная работа при изменении расстояния от d1 до d2 определится как
![]() . (3)
. (3)
3. Установим взаимосвязь расстояния между пластинами и ёмкости
![]() , (4)
, (4)
![]() . (5)
. (5)
4. Подставим уравнение (5) в формулу работы (3)
![]() . (6)
. (6)
1.7.17. Напряжение U1 = 100 B на круглых пластинах воздушного конденсатора радиусом R = 0,5 см увеличили до U2 = 200 В, а пластины развели на 25% от первоначальной величины d1 = 0,5 мм. Определить изменение заряда Dq на обкладках.
Решение
1. В данном случае конденсатор является плоским, поэтому его ёмкость для двух положений пластин определится как
![]() . (1)
. (1)
2. Подставим в уравнения (1) значение электрической ёмкости, выраженное через напряжение на обкладках и заряд конденсатора С = Q/U
![]() . (2)
. (2)
3. Разрешим уравнения (2) относительно зарядов и определим их разность
![]() , (3)
, (3)
![]() . (4)
. (4)
![]() . (5)
. (5)
1.7.18. Пластины плоского воздушного конденсатора несут заряды + 3Q и – Q. Определить разность потенциалов между пластинами, если расстояние между ними d, а их площадь - s.
Решение
1. Будем исходить из того, что напряжённость электрического поля между двумя параллельными заряженными пластинами определяется уравнением
![]() , (1)
, (1)
где  - напряжённость результирующего поля, определяемая в виде суперпозиции полей, создаваемых каждой из пластин.
- напряжённость результирующего поля, определяемая в виде суперпозиции полей, создаваемых каждой из пластин.
2. Геометрическая сумма напряжённостей полей создаваемых пластинами, в сочетании с уравнением (1), позволяют определить искомую разность потенциалов
![]() . (2)
. (2)
![]() , (3)
, (3)
![]() . (4)
. (4)
|
1.7.19. Плоский воздушный конденсатор погружают в жидкий диэлектрик с диэлектрической проницаемостью e2 двумя способами, показанными на рисунке. Во сколько раз, при этом, меняется ёмкость конденсатора.
Решение
1. Когда в жидкий диэлектрик погружена половина площади обоих пластин, то такой сложный конденсатор можно рассматривать как две электрические ёмкости, соединённые параллельно
![]() , (1)
, (1)
где e1 = 1 - диэлектрическая проницаемость воздуха, e2 - диэлектрическая проницаемость жидкого диэлектрика.
2. Изменение ёмкости для рассмотренного выше случая составит
![]() , (2)
, (2)
где С0 = e0e1s/d - электрическая ёмкость воздушного конденсатора.
3. При погружении в диэлектрик одной пластины образуется сложная ёмкость, которую можно представить в виде двух последовательно соединённых конденсаторов С2,1 и С2,2
 , (3)
, (3)
![]() . (4)
. (4)
4. Отношение ёмкостей в этом случае определится уравнением
![]() . (5)
. (5)
5. Определим далее отношение ёмкостей С2 и С1
 . (6)
. (6)
|
1.7.20. В отсутствии силы тяжести плоский воздушный конденсатор с пластинами площадью s и расстоянием между ними d1 подключён к источнику с электродвижущей силой e. К нижней пластине плотно прижата проводящая пластина массой m и толщиной d. С какой скоростью пластина ударится о верхнюю обкладку, если её отпустить?
Решение
1. На проводящей пластине, прижатой к нижней обкладке, индуцируется электрическое поле, причём отрицательные заряды будут концентрироваться со стороны нижней обкладки, а положительные - на противоположной. Так как пластина прижата плотно к обкладке и расположение её несимметрично, то часть электронов обкладки перейдёт на пластину, заряд которой можно определить как
![]() , (1)
, (1)
где С = e0s/(d1 – d2) - ёмкость воздушного конденсатора, образованного металлической пластиной и верхней обкладкой, e* - ЭДС источника тока.
2. Отрицательно заряженная металлическая пластина будет притягиваться к верхней положительно заряженной обкладке конденсатора. Вследствие второго закона Ньютона, наличие силы, действующей на массу, должно неминуемо привести к её движению. Движение пластины описывается законом сохранения энергии, в частности, теоремой об изменении кинетической энергии. Работа, совершаемая силами электрического поля равна изменению кинетической энергии пластины. С учётом неподвижности пластины в начальный момент времени, сказанное выше, можно представить следующим образом
![]() , (2)
, (2)
откуда скорость пластины в момент достижения верхней обкладки определится уравнением
![]() . (3)
. (3)
|
1.7.21. Во сколько раз изменится ёмкость плоского воздушного конденсатора с пластинами площадью s1 и расстоянием между ними d1, если параллельно обкладкам внести парафиновую пластину площадью s2 = s1/2 и толщиной d2 = d1/2?
Решение
1. В данном случае, при внесении пластины, ёмкость можно представить как три конденсатора, с последовательным и параллельным включением. Электроёмкость конденсатора, образованного пластинами и воздушным промежутком определяется как
![]() . (1)
. (1)
2. При внесении пластины с воздушным промежутком над ней представляет собой два последовательно соединённых конденсатора С2,1 и С2,2, и параллельную ёмкость С2,3
![]() , (2)
, (2)
где ![]() .
.
3. Подставим значение ёмкостей С2,1, С2,2 и С2,3 в уравнение (2)
 . (3)
. (3)
4. Поделим уравнение (3) на уравнение (1)
![]() . (4)
. (4)
1.7.22. Две концентрические металлические сферы радиусами R1 = 2 см и R2 = 2,1 см образуют сферический конденсатор. Пространство между сферами заполнено парафином с диэлектрической проницаемостью e = 2. Найти ёмкость сферического конденсатора.
|
Решение
1. Электрическая ёмкость сферического конденсатора определяется уравнением
![]()
|
1.7.23. Определить ёмкость конденсаторного соединения, ели С1 = С2 = С3 = С4 = С5 = 1 мкФ
Решение
|
1. Так как все конденсаторы задействованные в рассматриваемой схеме одинаковые, то потенциалы точек 2 и 4 будут тоже одинаковыми, а это значит, что при подключении батареи к источнику тока конденсатор С5 заряжаться не будет. В этой связи приведенную схему можно упростить.
2. В отсутствии конденсатора С5 схема представляет собой комбинацию последовательного и параллельного включения
![]() , (1)
, (1)
![]() . (2)
. (2)
3. По условию задачи все ёмкости одинаковые по величине, поэтому введём обозначение С1 = С2 = С3 = С4 = С, тогда
![]() . (3)
. (3)























