МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

Государственное образовательное учреждение высшего профессионального образования

«НАУЧНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

УТВЕРЖДАЮ:

И. о. зам. проректора-директора по химико-технологическому направлению

__________________

«____»__________ 2010

обработкА экспериментальных данных методами Лагранжа и Ньютона

Методические указания к выполнению лабораторной работы по дисциплине «Информатика» для студентов 1–го курса направлений 240100 «Химическая технология», 241000 «Энерго-и ресурсосберегающие процессы в химической технологии, нефтехимии и биотехнологии» и 240700 «Биотехнология»

Составитель

Томск 2010

УДК 681.5

«Обработка экспериментальных данных методами Лагранжа и Ньютона».

Методические указания к выполнению лабораторной работы по дисциплине «Информатика» для студентов 240100 «Химическая технология», 241000 «Энерго-и ресурсосберегающие процессы в химической технологии, нефтехимии и биотехнологии» и 240700 «Биотехнология»: - Томск: изд. ТПУ, 2010. – 16 с.

Составитель:

Рецензент, к. х.н.

Методические указания рассмотрены и рекомендованы методическим семинаром кафедры химической технологии топлива

" ___ " __________2010 года

Зав. кафедрой

Цель работы

1.  Научится строить интерполяционные многочлены Лагранжа и Ньютона для таблично заданной функции.

2.  Составить программу для расчета по формуле Лагранжа и определить численное значение полинома в заданных точках.

3.  Определить значение полинома Ньютона в заданных точках.

4.  Сравнить методы Лагранжа и Ньютона, используемые для обработки экспериментальных данных.

МЕТОДЫ ОБРАБОТКИ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

1. Понятие о приближении функции

При исследовании химических и химико-технологических процессов, как правило, возникает необходимость в обработке и анализе данных, полученных в эксперименте, с последующим применением результатов обработки при моделировании и проектировании реальных процессов. Пусть дана некоторая функция y=f(x). Например, это функция выхода продуктов реакции от концентрации исходного компонента. Это означает, что любому значению х (концентрации исходного компонента) ставится в соответствие значение y (выход продукта реакции). На практике часто оказывается, что найти это значение достаточно сложно: функция f(x) является решением сложной задачи (сложный хроматографический анализ) или f(x) измеряется в дорогостоящем эксперименте. В этом случае вычисляют небольшую таблицу значений выходного параметра от аргумента и по некоторым точкам строят функцию y=f(x) , где х – концентрация исходного компонента, y – концентрация продукта реакции.

Задача о приближении (аппроксимации) функции ставится следующим образом. Функцию f(x), где х изменяется в некоторой области, требуется приближенно заменить (аппроксимировать) некоторым многочленом Pm (x) так, чтобы отклонение Pm (x) от f(x) в заданной области было наименьшим. Полином Pm (x) при этом называется аппроксимирующим. Для практики важен случай аппроксимации функции многочленом степени m

Pm (x)=a0 + a1x + a2x2 + amxm . (1)

Коэффициенты a0, a1, ... , am должны подбираться так, чтобы отклонение многочлена от данной функции было наименьшим, а следовательно, задача о приближении функции состоит в определении a0, a1, ... , am полинома (5.1).

Если приближение строится на заданном дискретном множестве точек xi , то аппроксимация называется точечной. К ней относятся интерполирование, среднеквадратичное приближение, равномерное приближение и т. д.

2. Интерполирование

В инженерных расчетах часто требуется установить функцию f(x) для всех значений х отрезка [a, b] , если известны ее значения в некотором конечном числе точек этого отрезка. Одним из способов приближения функции является интерполяции.

Задача интерполяции может возникнуть в практике инженера при

-  интерполировании табличных данных;

-  получении функциональной зависимости по экспериментальным данным, представленным в табличной форме;

-  замене сложной с вычислительной точки зрения функции, более простой зависимостью;

-  при дифференцировании и интегрировании.

Постановка задачи.

Пусть на отрезке [x0,xn] заданы n+1 точки x0, x1, x2,...,xn, называемые узлами интерполяции, и значения некоторой интерполируемой функции y=f(x) в этих точках, т. е. имеется таблица экспериментальных значений функции y=f(x): y0, y1, y2.....yn.

y0=f(x0); y1=f(x1); ...; yn=f(xn). (2)

Требуется найти значения этой функции для промежуточных значений аргумента, не совпадающих с приведенными в таблице. Получить аналитическое выражение функции y= f(x) по таблице ее значений (5.2) в большинстве случаев невозможно. Поэтому вместо нее строят другую функцию, которая легко вычисляется и имеет ту же таблицу значений, что и f(x), т. е.

Pm(x0)=f(x0)=y0,

..........................

.......................

Pm(xi)=f(xi)=yi , где i = 0,1,2, ... , n.

Такую задачу называют задачей интерполирования. Точки xi называются узлами интерполяции, функция f(x) - интерполируемой функцией, многочлен Pm(x) - интерполяционным многочленом. Задачей интерполяции, в узком смысле слова, считают нахождение приближенных значений табличной функции при аргументах x, не совпадающих с узловыми. Если значение аргумента x расположено между узлами x0xxn , то нахождение приближенного значения функции f(x) называется интерполяцией, если аппроксимирующую функцию вычисляют вне интервала [x0,xn], то процесс называют экстраполяцией. Происхождение этих терминов связано с латинскими словами inter - между, внутри, pole - узел, extra - вне.

Графически задача интерполирования заключается в том, чтобы построить такую интерполирующую функцию, которая бы проходила через все узлы интерполирования (рис.5.1).

Рис.1

Близость интерполяционного многочлена к заданной функции состоит в том, что их значения совпадают на заданной системе точек.

При решении задачи интерполирования обычно принимается, что:

-  интерполируемая функция непрерывна на отрезке [a, b] и в каждой точке имеет конечные производные любого порядка;

-  узлы интерполирования отличны друг от друга.

2.1. Линейная интерполяция

Простейшим и часто используемым видом интерполяции является линейная интерполяция. Она состоит в том, что заданные точки xi, yiпри i=0,1,2,... n соединяются прямолинейными отрезками и функцию f(x) можно приближенно представить ломаной с вершинами в данных точках.

Уравнения каждого отрезка ломаной в общем случае разные. Поскольку имеется n интервалов (xi-1,xi), то для каждого из них в качестве уравнения интерполяционного многочлена используется уравнение прямой, проходящей через две точки. В частности, для i-го интервала можно написать уравнение прямой, проходящей через точки (xi-1,yi-1) и (xi,yi), в виде

= .

Отсюда

y=aix+bi, xi-1 x xi , (4)

ai = , bi = y i-1- ai xi-1.

Следовательно, при использовании линейной интерполяции сначала нужно определить интервал, в который попадает значение аргумента x, а затем подставить его в формулу (5.4) и найти приближенное значение функции в этой точке.

2.2. Интерполяционный многочлен Лагранжа

Пусть функция f(x) задана таблично. Это могут быть, например, значения концентраций продуктов реакции в зависимости от температуры, полученные экспериментально.

Значения x0,x1,..., xn называются узлами таблицы. Считаем, что узлы в общем случае не являются равноотстоящими (шаг таблицы неравномерный).

Построим интерполяционный многочлен на отрезке [x0,xn]. Запишем искомый многочлен в виде

Pm(x)=a0 +a1x + a2x2 + amxm . (5)

Геометрически задача интерполирования сводится к построению кривой через заданные точки.

Аналитически задача сводится к решению системы уравнений

(6)

Для определения коэффициентов многочлена (5) необходимо располагать n+1 узловой точкой.

Чтобы система уравнений имела единственное решение, необходимо, чтобы количество неизвестных коэффициентов полинома (аj) – m+1 - равнялось количеству уравнений n+1или m=n.

Пусть в n+1-ой точках x0, x1,..., xn определены значения y0, y1,..., yn. Требуется построить многочлен Pn(x), принимающий в узловых точках заданные значения yi, т. е. такой, что

Pn(xi) = yi, i= 0,1, ...,n.

Лагранж предложил следующую форму интерполяционного полинома

, (7)

где Li(x) - множитель Лагранжа, имеющий вид:

. (8)

Следовательно, формулу Лагранжа можно представить в виде:

Pn(x)=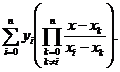 (9)

Числитель и знаменатель не должны включать в себя значения

x =xi, так как результат будет равен нулю. В развернутом виде формулу Лагранжа можно записать:

(10)

Блок-схема метода Лагранжа приведена на рис.2.

Пример 1. Для функции y=sinpx построить интерполяционный полином Лагранжа, выбрав узлы: x0, x1, x2.

Применяя формулу (10), получим:

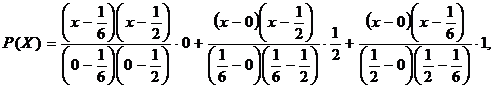
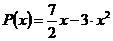
Пример 2. Дана таблица значений теплоёмкости вещества в зависимости от температуры Cp =f(T).

Вычислить значение теплоёмкости в точке Т=450 К.

Для решения воспользуемся формулой (5.10).

Значение теплоемкости при температуре 450 К получим:

.

Рассмотрим понятие конечных разностей.

Пусть задана функция y=f(x) на отрезке [x0,xn], который разбит на n одинаковых отрезков (случай равноотстоящих значений аргумента). Dx=h=const. Для каждого узла x0, x1=x0+h, ..., xn=x0+n×h определены значения функции в виде:

f(x0)=y0, f(x1)=y1, ..., f(xn)=yn. (11)

Введем понятие конечных разностей.

Конечные разности первого порядка

Dy0 = y1 – y0;

Dy1 = y2 – y1;

Dyn-1 = yn – yn-1.

Конечные разности второго порядка

D2y0 = Dy1 – Dy0;

D2y1 = Dy2 – Dy1;

D2yn-2 = Dyn-1 – Dyn-2.

Аналогично определяются конечные разности высших порядков:

Dky0 = Dk-1y1 – Dk-1y0;

Dky1 = Dk-1y2 – Dk-1y1;

DkyI = Dk-1yi+1 – Dk-1yI, i = 0,1,...,n-k.

Конечные разности функций удобно располагать в таблицах, которые могут быть диагональными (табл.1) или горизонтальными (табл.2.

Таблица 1.

Диагональная таблица

Таблица 2.2

Горизонтальная таблица

Первая интерполяционная формула Ньютона

Пусть для функции y = f(x) заданы значения yi = f(xi) для равностоящих значений независимых переменных:

xn = x0 +nh, где h - шаг интерполяции.

Необходимо найти полином Pn(x) степени не выше n, принимающий в точках (узлах) xi значения:

Pn (xi) = yi , i=0,...,n. (12)

Интерполирующий полином ищется в виде:

(13)

Задача построения многочлена сводится к определению коэффициентов аi из условий:

Pn(x0)=y0,

Pn(x1)=y1,

Pn(xn)=yn.

Полагаем в (5.13) x = x0, тогда, т. к. второе, третье и другие слагаемые равны 0,

Pn(x0) = y0 = a0; a0=y0.

Найдем коэффициент а1.

При x = x1 получим:

Pn (x1) = y1 = y0 +a1(x1 – x0);

y1 = y0 +a1(x1 – x0),

= .

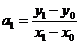Для определения а2, составим конечную разность второго порядка.

При x = x2 получим:

Pn(x2) = y2 = y0+ (x2 – x0)+a2(x2 – x0)(x2 – x1) = y0+2Dy0+a22h2,

a2 = = = =

= = =.

Аналогично можно найти другие коэффициенты. Общая формула имеет вид.

(15)

Подставляя эти выражения в формулу (5.13), получаем:

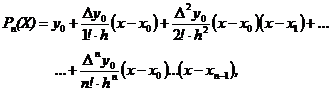(16)

где xi ,yi – узлы интерполяции; x – текущая переменная; h – разность между двумя узлами интерполяции h – величина постоянная, т. е. узлы интерполяции равноотстоят друг от друга.

Этот многочлен называют интерполяционным полиномом Ньютона для интерполяции в начале таблицы (интерполирование «вперед») или первым полиномом Ньютона.

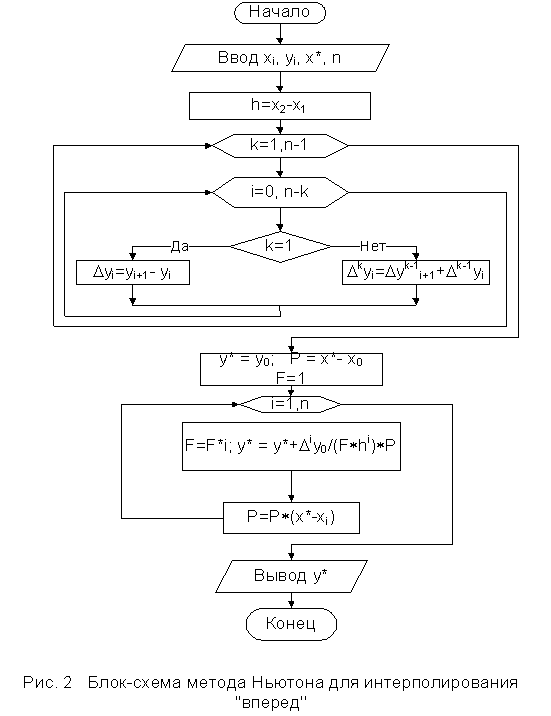
Блок-схема алгоритма метода Ньютона для интерполирования «вперед» приведена на рис. 2.

Таблица 3

Построить интерполяционный многочлен Ньютона для заданных значений функции.

n=3; h=100.

Составим таблицу конечных разностей функции.

Таблица 4

Воспользуемся формулой (16):

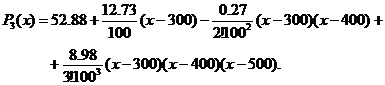
После выполнения преобразований получим интерполяционный многочлен вида:

Полином имеет третью степень и дает возможность вычисления при помощи найденной формулы значения y для неизвестного x .

Пример 4.

В табл. (3) приведены значения теплоемкости в зависимости от температуры. Определить значение теплоёмкости в точке Т=450, К.

Воспользуемся первой интерполяционной формулой Ньютона. Конечные разности рассчитаны в предыдущем примере, табл. 4, запишем интерполяционный многочлен при x=450 К.

Таким образом, теплоемкость при температуре 450 К будет

Ср(450)=71,31Дж/(моль × К).

Значение теплоемкости при Т=450 К получили такое же, что и рассчитанное по формуле Лагранжа.

Вторая интерполяционная формула Ньютона

Для нахождения значений функций в точках, расположенных в конце интервала интерполирования, используют второй интерполяционный полином Ньютона. Запишем интерполяционный многочлен в виде

(18)

Коэффициенты а0,а1,..., аn определяем из условия:

Pn (xi ) = yi , i=0,...n.

Полагаем в (5.18 ) x = xn, тогда

Полагаем x=xn-1, тогда

Pn(xn-1)=yn-1=yn+a1(xn-1 – xn) , h=xn – xn-1 ,

следовательно,

.

Если x=xn-2 , то

.

Аналогично можно найти другие коэффициенты многочлена (18).

,

...........................

.

Подставляя эти выражения в формулу (5.18), получим вторую интерполяционную формулу Ньютона или многочлен Ньютона для интерполирования «назад».

(20)

Произведя замену в (19) , получим

. (21)

Это вторая формула Ньютона для интерполирования «назад».

Пример 5.

Вычислить теплоемкость (табл. 3) для температуры Т=550 К.

Воспользуемся второй формулой Ньютона (19) и соответствующими конечными разностями (табл.4)

Следовательно, значение теплоемкости при температуре 550 К равно:

Ср(550)=97,01 Дж/(моль К).

Варианты заданий

Вариант 1

С помощью интерполяционного многочлена найти значения У в точках Х равных: Х=0,2; Х=2,0

Вариант 2

С помощью интерполяционного многочлена найти значения У в точках Х равных: Х=1,9; Х=3,7

Вариант 3

С помощью интерполяционного многочлена найти значения У в точках Х равных: Х=0,17; Х=1,91

Вариант 4

С помощью интерполяционного многочлена найти значения У в точках Х равных: Х=1,9; Х=3,7

Вариант 5

С помощью интерполяционного многочлена найти значения У в точках Х равных: Х=6,2; Х=7,6

Вариант 6

С помощью интерполяционного многочлена найти значения У в точках Х равных: Х=0,75; Х=2,53

Вариант 7

С помощью интерполяционного многочлена найти значения У в точках Х равных: Х=0,48; Х=0,87

Вариант 8

С помощью интерполяционного многочлена найти значения У в точках Х равных: Х=0,48; Х=0,9

Вариант 9

С помощью интерполяционного многочлена найти значения У в точках Х равных: Х=0,5; Х=0,9

Вариант 10

С помощью интерполяционного многочлена найти значения У в точках Х равных: Х=0,5; Х=0,93

Порядок выполнения работы

1.  Записать формулу Лагранжа и Ньютона для таблично заданной функции.

2.  Составить программу для расчета по формуле Лагранжа и вычислить численное значение полинома в заданных точках.

3.  Составить программу для расчета по формуле Ньютона и вычислить численное значение полинома в заданных точках.

4.  Сравнить методы Лагранжа и Ньютона, используемых для обработки экспериментальных данных.

5.  Обсудить результаты. Сделать выводы по работе.

6.  Составить отчет.

ЛИТЕРАТУРА

5.  , , Кобельков методы.- М.:Наука,1987.-600с.