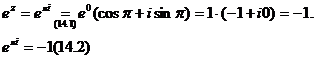Аксиомы кольца, аксиомы поля. Примеры колец и полей (поле из двух элементов).
Пусть R - непустое множество. В R введены 2 операции: сложение и умножение. Эти операции бинарны: +: 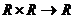 ,
,  ,
,
Аксиомы кольца: Множество R с операциями «+» и «*» называется кольцом, если выполняются аксиомы. Аксиомы сложения:
1. (a + b) + c = a + (b + c), ![]() (Ассоциативность сложения).
(Ассоциативность сложения).
2. a + b = b + a, (Коммутативность сложения).
(Коммутативность сложения).
3. ![]() .
.
4. ![]() ,
, ![]() - противоположный к a элемент (существование противоположного элемента).
- противоположный к a элемент (существование противоположного элемента).
Аксиома умножения:
5. 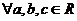 ,
,  (Ассоциативность умножения).
(Ассоциативность умножения).
6.  (Дистрибутивность сложения и умножения).
(Дистрибутивность сложения и умножения).
Дополнительные аксиомы:
7. 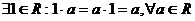 . Аксиома единицы
. Аксиома единицы
Если в кольце R выполняется 8., то R – коммутативное кольцо.
Примеры:
1)  .
.
«+»: 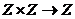 ;
;
«*»: 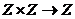 ,
,
Z – коммутативное кольцо с единицей, т. к. выполняется 1 – 8.
2) Q, R – коммутативные кольца с единицей.
3)  . Определены операции сложения и умножения матриц, 1 – 6 выполняются в силу свойств этих операций
. Определены операции сложения и умножения матриц, 1 – 6 выполняются в силу свойств этих операций ![]() - кольцо. 7 – выполняется, т. к. E является единицей кольца. 8 вообще говоря не выполняется для
- кольцо. 7 – выполняется, т. к. E является единицей кольца. 8 вообще говоря не выполняется для ![]() .
.  некоммутативное кольцо с единицей.
некоммутативное кольцо с единицей.
4)  множество чисел,
множество чисел, ![]() . 1 – 6 выполняются,
. 1 – 6 выполняются, ![]() кольцо, 8 – выполняется
кольцо, 8 – выполняется ![]() - коммутативное кольцо. 7 - ? Пусть mk, (
- коммутативное кольцо. 7 - ? Пусть mk, (![]() ) – единица в mZ, тогда
) – единица в mZ, тогда ![]() , но 1 не кратна m, если
, но 1 не кратна m, если ![]() , то mZ не имеет единицу.
, то mZ не имеет единицу.
Аксиомы поля:
Z - коммутативное кольцо с единицей, Q, R – тоже. Отличие: в Z не для всякого ненулевого элемента есть обратный из этого кольца. Но для Q, R условие обратимости ненулевых элементов выполняется.
Определение: Поле – коммутативное кольцо с единицей, отличной от 0, в котором всякий ненулевой элемент обратим, т. е. выполняется 9 – аксиома поля:
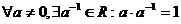 . Всего существует 9 аксиом поля. Примеры полей: Q, R.
. Всего существует 9 аксиом поля. Примеры полей: Q, R.
Пример2: Пусть k – поле, тогда по определению: ![]() (число элементов).
(число элементов).
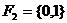 , + и * задаются таблицами:
, + и * задаются таблицами: 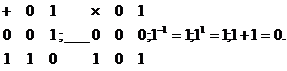
![]() поле, состоящее из 2 – х элементов. Существует ли поле из 6 - элементов.
поле, состоящее из 2 – х элементов. Существует ли поле из 6 - элементов.
Поле комплексных чисел. Алгебраическая форма комплексного числа: сложение, умножение, деление комплексных чисел.
 (действительных корней нет),
(действительных корней нет), ![]() мнимая единица, т. е.
мнимая единица, т. е. ![]() .
.
Определение: Полем комплексных чисел называется минимальное поле, содержащие все действительные числа и мнимую единицу ![]() .
.
Структура поля комплексных чисел. Обозначение C.
Рассмотрим множество:  Т. к. C – поле и
Т. к. C – поле и ![]() (по определению) и
(по определению) и ![]() - тоже, значит числа вида
- тоже, значит числа вида ![]() . Если докажем, что
. Если докажем, что ![]() - поле, то
- поле, то ![]() - поле, содержащее
- поле, содержащее ![]() и все действительные числа, т. к.
и все действительные числа, т. к.  , тогда в силу минимальности C получим, что
, тогда в силу минимальности C получим, что ![]() .
.
Цель: доказать, что ![]() - поле, откуда,
- поле, откуда, ![]() .
.
Теорема: ![]() поле.
поле.
Док-во: Введём в ![]() операции сложения и умножения чисел:
операции сложения и умножения чисел:

 (Мотивировка правила умножения).
(Мотивировка правила умножения). ![]() .
.
 .
.
Проверим выполнение аксиом 1-9 поля:
1. 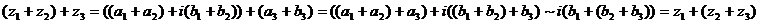
Ассоциативность сложения выполняется..
2. 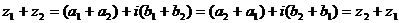 .
.
3.  .
.
4.  , то в качестве противоположного
, то в качестве противоположного ![]() . Все аксиомы сложения выполнены.
. Все аксиомы сложения выполнены.
5. 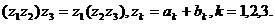
6. 

7.  - единица в
- единица в ![]() .
.
8. 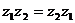 (в силу определения операции умножения), т. е.
(в силу определения операции умножения), т. е. ![]() - коммутативное кольцо с единицей.
- коммутативное кольцо с единицей.
9. Пусть 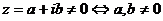 одновременно.
одновременно. ![]() т. к.
т. к. ![]()

Итак, если  .
.
Любой ненулевой элемент обратим в ![]() аксиома поля выполнена,
аксиома поля выполнена, ![]() поле. ЧТД.
поле. ЧТД.
Комплексное число:  - алгебраическая запись числа
- алгебраическая запись числа ![]()
![]() называется действительной частью:
называется действительной частью: ![]()
![]() называется мнимой частью:
называется мнимой частью: ![]()
![]() .
.
Извлечение квадратного корня из комплексного числа в алгебраической форме.

Сопряжённое комплексное число и его свойства.
Пусть  . Тогда число вида
. Тогда число вида ![]() называется сопряжённой к данному числу
называется сопряжённой к данному числу ![]() , т. е.
, т. е.
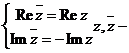 симметричны относительно оси Re.
симметричны относительно оси Re.
Свойства сопряжённого комплексного числа:
1. 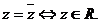
2.  (с точностью до
(с точностью до ![]() ).
).
3. 
4. 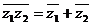 .
.
5. 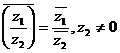 .
.
6. 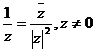 .
.
7.  .
.
Изображение комплексных чисел на плоскости, модуль и аргумент комплексного числа.
 , то z изображается точкой на плоскости с координатой (a, b).
, то z изображается точкой на плоскости с координатой (a, b).
Пусть z – комплексное число. Определение: Модулем числа z называется длина радиус вектора точки, изображающей данное число z. Обозначение: ![]() .
.
Модуль комплексного числа – корень квадратный из суммы квадратов его действительной и мнимой части. ![]()
Определение: Аргументом числа z называется угол (ориентированный) между радиус-вектором точки, изображающей комплексное число z и положительное направление действительной оси. Обозначение: ![]() . Аргумент определяется неоднозначно, а именно с точностью до слагаемых вида
. Аргумент определяется неоднозначно, а именно с точностью до слагаемых вида 
Тригонометрическая форма комплексного числа: умножение и деление чисел в тригонометрической форме.
Пусть  тогда
тогда ![]() - проекция на ось
- проекция на ось ![]() .
. ![]() проекция на ось Im =
проекция на ось Im = ![]()
 (алгебраическая запись), то
(алгебраическая запись), то ![]() .
.

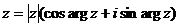 .
.

Обратно: 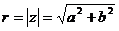 (длина вектора).
(длина вектора). ![]()
Однозначно угол определяется, если по знакам Rez и Imz указать четверть, в которой находится ![]()

Умножение и деление КЧ в тригонометрической форме:
I. Задача: ![]() Найти:
Найти: ![]() , если
, если ![]() .
.
Решение: 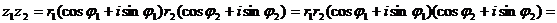
 .
.
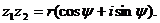
Условие равенства КЧ:
А) 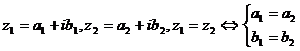 .
.
Б) 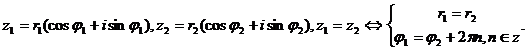
Сравнивая записи для ![]() получаем, что
получаем, что ![]()
 .
.
Правило умножения КЧ:
При умножении КЧ модули перемножаются, а аргументы складываются.
II.

С другой стороны:  , тогда
, тогда 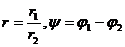 .
.
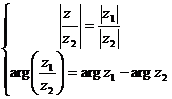
Правила деления: Модуль частного КЧ равен частному модулей делимого и делителя, а аргумент частного есть разность аргументов делимого и делителя.
Формула Муавра.
Теорема: Пусть  , тогда
, тогда  (если
(если ![]() , то
, то ![]() ) - формула Муавра.
) - формула Муавра.
Док-во:
1)  , то
, то ![]() .
.
Левая часть формулы Муавра: ![]() .
.
2) Пусть 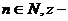 любое. Применим ММИ по n.
любое. Применим ММИ по n.
а) n = 1, то 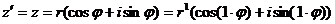 , т. е. формула верна.
, т. е. формула верна.
Б) Пусть при n = k формула Муавра верна.
В) n = k + 1.
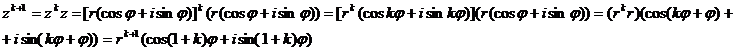
т. е. формула верна при n = k + 1, значит при всех ![]() .
.
3) n – отрицательный, т. е. 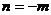 , где
, где ![]()
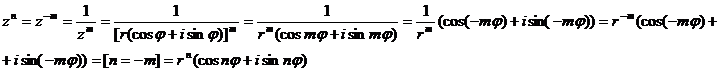 ЧТД.
ЧТД.
Извлечение корня n-й степени из комплексного числа.
Определение: Число ![]() называется корнем
называется корнем ![]() й степени из КЧ z, если
й степени из КЧ z, если ![]() . Другими словами, найти все корни степени n из z – это значит, что необходимо решить уравнение
. Другими словами, найти все корни степени n из z – это значит, что необходимо решить уравнение ![]() .
.
Теорема: Существует ровно n корней степени n из КЧ ![]() , где
, где ![]() , где (
, где (![]() обычный арифметический корень из положительного числа r).
обычный арифметический корень из положительного числа r).
Док-во: Будем искать решение уравнения ![]() в виде
в виде ![]() , (
, (![]() надо определить).
надо определить).
Тогда 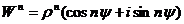 - формула Муавра. По условию:
- формула Муавра. По условию: ![]() . Используем условия равенства КЧ в тригонометрической форме:
. Используем условия равенства КЧ в тригонометрической форме:
 (
(![]() положительное число,
положительное число, ![]() как модуль).
как модуль). 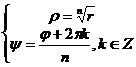 .
.
Итак, любой корень уравнения ![]() имеет вид:
имеет вид: ![]() . Докажем, что среди
. Докажем, что среди ![]() только n различных чисел.
только n различных чисел.
1. Покажем, что ![]() различны. Предположим, что
различны. Предположим, что ![]() , если
, если ![]() , т. е.
, т. е. ![]()

Но  , т. к.
, т. к.  .
.
 Среди чисел
Среди чисел ![]() - нет ни одного, которое делится на n.
- нет ни одного, которое делится на n.
![]() получено противоречие. Значит
получено противоречие. Значит ![]() - различные числа.
- различные числа.
II. Покажем, что ![]() для произведения целого k совпадает с одним из чисел
для произведения целого k совпадает с одним из чисел ![]() . Разделим k на n с остатком, т. е.
. Разделим k на n с остатком, т. е. ![]() , где
, где
![]() [остаток]< n – 1.
[остаток]< n – 1.

т. е. числа 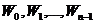 исчерпывают все корни степени n из z. ЧТД.
исчерпывают все корни степени n из z. ЧТД.
Замечание: Все корни степени n из z имеют один и тот же модуль ![]() находятся на окружности данного радиуса. Аргументы 2 – х соседних корней, т. е.
находятся на окружности данного радиуса. Аргументы 2 – х соседних корней, т. е. ![]() отличаются на
отличаются на ![]() (n – ная часть угла полного поворота). Это означает, что корни находятся в вершинах правильного n-угольника, вписанного в данную окружность.
(n – ная часть угла полного поворота). Это означает, что корни находятся в вершинах правильного n-угольника, вписанного в данную окружность.
Корни из единицы и их свойства.
Определение: Решением уравнения ![]() называется корнями n – ной степени из 1.
называется корнями n – ной степени из 1.

 обозначение.
обозначение.
Корни n – ной степени из 1 изображаются вершинами правильного n – угольника, вписанного в единичную окружность с вершиной (1; 0).
Лемма:
А) Произведение корней n – ной степени из единицы – это корень n – ной степени из 1.
Б) Обратный элемент к корню n – ной степени из 1 – корень n – ной степени из 1.
В) Целая степень корня n – ной степени из 1 – корень n – ной степени из единицы.
Док-во:
А)  корни степени n из 1, т. е.
корни степени n из 1, т. е. ![]() .
.
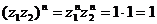 .
.
По определению  корень степени n из 1.
корень степени n из 1.
Б) z – корень n – ной степени.

![]() корень n – ной степени из 1.
корень n – ной степени из 1.
В)
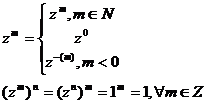
Т. е. ![]() корень n – ной степени из 1.
корень n – ной степени из 1.
Замечание: Если ![]() - корни n – ной степени из 1, то
- корни n – ной степени из 1, то ![]() , т. к.
, т. к. ![]()
Т. е. все корни n – ной степени из 1 можно представить как степени ![]() .
.
Первообразные корни, критерий первообразности корня.
Определение: Корень n – ной степени из 1 называется первообразным, если любой другой корень n – й степени из 1 можно представить в виде целой степени этого корня из 1.
В частности, ![]() является первообразным корнем степени n из 1,
является первообразным корнем степени n из 1, ![]() .
.
Примеры:

Т. е. ![]() - не является первообразным.
- не является первообразным. ![]() - первообразный.
- первообразный.
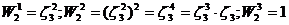 . Все корни 3 – й степени есть степени степени
. Все корни 3 – й степени есть степени степени ![]() , значит
, значит ![]() - первообразный.
- первообразный.

 первообразные,
первообразные, ![]() не являются первообразными.
не являются первообразными.
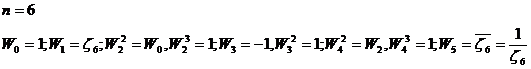 .
.
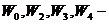 не первообразные,
не первообразные, ![]() первообразные.
первообразные.
Таблица первообразных корней:

Теорема (Критерий первообразности корня из 1.):
Корень n – ной степени из 1: 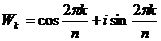 является первообразным тогда и только тогда, когда НОД (k, n) = 1, т. е. взаимно прост с n.
является первообразным тогда и только тогда, когда НОД (k, n) = 1, т. е. взаимно прост с n.
Док-во:
1. Пусть ![]() - первообразный, пусть d = НОД (k, n).
- первообразный, пусть d = НОД (k, n). ![]() - целый показатель.
- целый показатель.
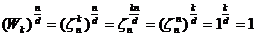 , т. е. остальные степени
, т. е. остальные степени ![]() будут совпадать с уже выписанными.
будут совпадать с уже выписанными.
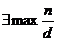 различных степеней
различных степеней ![]() . Но по условию,
. Но по условию, ![]() - первообразный, значит
- первообразный, значит ![]() имеет ровно n различных степеней.
имеет ровно n различных степеней.
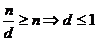 , но НОД
, но НОД  , т. е. k и n взаимно просты.
, т. е. k и n взаимно просты.
2. Пусть НОД (k, n) = 1.
Докажем, что ![]() имеет не менее n различных целых степеней. Рассмотрим множество:
имеет не менее n различных целых степеней. Рассмотрим множество:  . Покажем, что все элементы этого множества различны:
. Покажем, что все элементы этого множества различны: ![]() , где
, где ![]() .
.

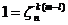 . Но
. Но ![]() тогда и только тогда, когда N кратно n, т. е. k (m - l) делится на n, но k и n взаимно просты
тогда и только тогда, когда N кратно n, т. е. k (m - l) делится на n, но k и n взаимно просты ![]() делится на n.
делится на n.

m – l кратно ![]() , т. е. m – l = 0, значит m = l.
, т. е. m – l = 0, значит m = l.
Итак, все элементы множества ![]() различны. По лемме все эти элементы являются корнями n – й степени из 1, т. е. любой корень n – й степени из 1 является целой степенью
различны. По лемме все эти элементы являются корнями n – й степени из 1, т. е. любой корень n – й степени из 1 является целой степенью ![]() .
.
![]() - является первообразным. ЧТД
- является первообразным. ЧТД
Экспонента комплексного числа. Формула Эйлера. Экспоненциальная форма комплексного числа.
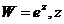 - КЧ.
- КЧ.
Сходимость в C.
Определение: Говорят, что последовательность КЧ ![]() сходится к КЧ z (или
сходится к КЧ z (или ![]() ), если
), если ![]() .
.
![]() - окрестность точки z. Это круг без границ, с центром в точке z, радиуса
- окрестность точки z. Это круг без границ, с центром в точке z, радиуса ![]() .
.
Утверждение 1: Число  является пределом последовательности
является пределом последовательности ![]() тогда и только тогда, когда
тогда и только тогда, когда ![]() .
.
Док-во:
1 – й шаг (Оценки)

Аналогично: 
2. Сравним квадраты: 

2 – й шаг: Пусть 
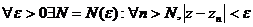 , по шагу 1:
, по шагу 1: ![]() и
и 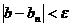 , т. е. выполняется определение предела для вещественных последовательности
, т. е. выполняется определение предела для вещественных последовательности ![]() и
и ![]() , т. е.
, т. е. 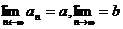 .
.
Док-во:
3 - й шаг: Пусть 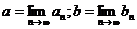 .
.
Выбираем ![]() , тогда для
, тогда для  .
.
Для  .
.
Выбираем  , тогда
, тогда 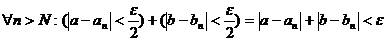 .
.
Используем шаг 1 – й для ![]() .
.
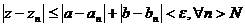 , тогда
, тогда 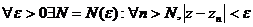 ,т. е. по определению
,т. е. по определению ![]() . ЧТД.
. ЧТД.
Утверждение 2:  . (Вновь с комплексной последовательности
. (Вновь с комплексной последовательности ![]() связаны 2 вещественные последовательности
связаны 2 вещественные последовательности ![]() .)
.)
Если  и
и  , то
, то  .
.
Док-во:  ,
,  .
.
 . Покажем, что
. Покажем, что ![]() :
:
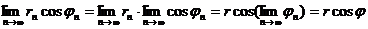 .
.
Аналогично,  . Тогда по утверждению 1, имеем, что
. Тогда по утверждению 1, имеем, что ![]() , причём:
, причём:
 . ЧТД.
. ЧТД.
Определение: Пусть z – КЧ, тогда ![]() .
.
Теорема (Корректность определения.): ![]()
Док-во: 
Пусть  , тогда
, тогда 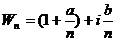 . Начиная с некоторого номера n:
. Начиная с некоторого номера n: ![]() , т. е.
, т. е. ![]() будет либо в I либо в IV четвертях, тогда
будет либо в I либо в IV четвертях, тогда ![]() .
.

Мы исследуем сходимость последовательности:  . По формуле Муавра:
. По формуле Муавра: ![]()
В силу утверждения 2 мы докажем сходимость нашей последовательности, если покажем, что 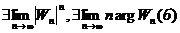 , (а) – (13.2).
, (а) – (13.2).

Существует ли 

Итак, показано, что  По утверждению 2,
По утверждению 2, ![]() , т. е.
, т. е. ![]() - определена корректно. ЧТД.
- определена корректно. ЧТД.
Следствие: В процессе доказательства теоремы был вычислен ![]() , а именно, если
, а именно, если ![]() , то
, то ![]() , т. е.
, т. е. ![]() - формула Эйлера.
- формула Эйлера.
Свойства функции: 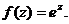
1.  , т. к.
, т. к.  - определена для
- определена для ![]()
2.  . (Если k – поле, то k \ {0} обозначается
. (Если k – поле, то k \ {0} обозначается ![]() .
. ![]() - все обратимые элементы.)
- все обратимые элементы.)
а)  (по формуле Эйлера)
(по формуле Эйлера)
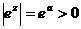 , т. к.
, т. к. ![]() , т. е.
, т. е. ![]() имеет ненулевой модуль, а значит отлично от 0.
имеет ненулевой модуль, а значит отлично от 0. ![]()
Пусть ![]() .
.
 , где
, где ![]() .
. 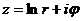 , то
, то 
Итак,  является экспонентой некоторого количественного z.
является экспонентой некоторого количественного z.
3.  периодическая функция.
периодическая функция.
Док-во: (Надо доказать, что) ![]() .
.
Рассмотрим комплексное число вида: ![]()
![]() .
.
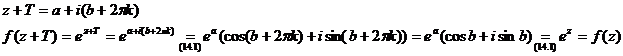 . ЧТД.
. ЧТД.
4. 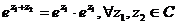 .
.
Док-во:
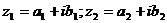 .
.
Левая часть равенства: ![]()
Правая часть:  = [правило умножения КЧ в тригонометрической форме.] =
= [правило умножения КЧ в тригонометрической форме.] = 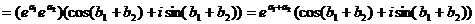 . Левая часть равна правой части, значит равенство верно. ЧТД.
. Левая часть равна правой части, значит равенство верно. ЧТД.
Следствие: (Экспоненциальная форма комплексного числа.)
Пусть ![]() (произвольное число). В тригонометрической форме
(произвольное число). В тригонометрической форме 
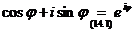 , тогда
, тогда  - экспоненциальная форма КЧ.
- экспоненциальная форма КЧ.
5. ![]() .
.