Устойчивость и расчет критических нагрузок балки прямоугольного сечения из нелинейного материала при чистом изгибе и растяжении

УСТОЙЧИВОСТЬ И РАСЧЕТ КРИТИЧЕСКИХ НАГРУЗОК БАЛКИ ПРЯМОУГОЛЬНОГО СЕЧЕНИЯ ИЗ НЕЛИНЕЙНОГО МАТЕРИАЛА ПРИ ЧИСТОМ ИЗГИБЕ И РАСТЯЖЕНИИ

,

Институт машиноведения УрО РАН, Екатеринбург, Россия

Введение. Возрастающие требования к достоверности методов оценки несущей способности и долговечности конструкций предопределяют необходимость учета в расчетах всех стадий деформирования материала, в том числе и состояние предразрушения. Эта стадия появляется вследствие диссипативных процессов, происходящих в материале при его деформировании, характеризуется существенным повреждением материала микропорами и микротрещинами и, следовательно, падением его несущей способности. С феноменологической точки зрения, этот эффект проявляется падающим участком диаграммы деформирования. Материал с такой диаграммой является реологически неустойчивым. Многие реальные материалы, такие как горные породы [1], ряд металлов [2] и даже лед [3], могут быть описаны именно моделями реологически неустойчивых материалов.

В процессе нагружения некоторого элемента механической конструкции потеря устойчивости деформирования этого элемента сопровождается разрушением материала микротрещинами. Однако наличие участков локальной потери устойчивости отдельного элемента не вызывает исчерпания устойчивости всей конструкции в целом вследствие геометрических связей, накладываемых другими элементами конструкции или внешними факторами. Поэтому учет дополнительного вклада неустойчивого элемента системы может быть существенным при расчете предельных нагрузок всей системы.

Растягивающая сила, приложенная к торцам балки, способствует отклонению нейтральной линии, где напряжения и деформации нулевые, от оси симметрии Ox. Однако в силу симметрии поперечного сечения Q не приводит к появлению в балке поперечных или тангенциальных напряжений, таким образом, модель остается одномерной при комбинированном нагружении растягивающей силы и изгибающего момента.

Полные деформации вычисляются по формуле . Здесь κ – кривизна центральной оси балки в результате изгиба и a – расстояние от оси симметрии Ox до нейтральной линии (рис. 2). На рисунке 2 также отмечены γ1 и γ2 – деформации крайних волокон балки наиболее сжатых и наиболее растянутых соответственно.

Свойства материала, из которого изготовлена балка, определяет полная диаграмма деформирования σ(ε), обладающая восходящей и падающей до нуля ветвями. Диаграмму характеризует функция , имеющая смысл касательного модуля. Ее знак определяет состояние материала: если , то имеет место упрочнение материала (восходящие участки диаграммы), если - разупрочнение (падающие участки).

В задаче о чистом изгибе и растяжении дифференциальные уравнения равновесия и условия совместности деформаций удовлетворяются тождественно.

Выпишем функцию полной энергии механической системы:

Здесь - потенциал напряжений, равный работе деформаций материального элемента, - работа растягивающей силы , распределенной по поперечному сечению c площадью и равнодействующей Q. - относительное удлинение балки вдоль продольной оси. Преобразуем выражение для потенциальной функции:

(1)

Вычислим частные производные функции (1) по параметрам состояния:

Приравнивая их нулю, получаем равенства

(2)

которые совпадают со статическими уравнениями равновесия и граничными условиями в задаче об изгибе и растяжении бруса, а именно равенство продольной силы в балке растяжению Q и равенство моменту внутренних сил приложенному изгибающему моменту M. Соотношения (2) также связывают параметры управления (прикладываемые растягивающее усилие Q и момент M) и параметры состояния (расстояние a от нейтральной линии и кривизна κ) в положениях равновесия.

2. Операторные уравнения равновесия. Соотношения (2) можно рассматривать в качестве операторных уравнений

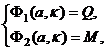(3)

с нелинейным векторным оператором , отображающим евклидово пространство состояний 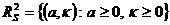в евклидово пространство управлений .

Уравнения (3) относительно пар переменных (a, κ) и (Q, M) определяют одну группу переменных через другую как неявную функцию. Если функции и непрерывно дифференцируемы по совокупности переменных и Якобиан отображения (детерминант матрицы Якоби), равный сильной производной отображения - производной по Фреше [6],

(4)

не равен нулю в некоторой точке из множества , тогда по теореме об обратном отображении [7] для и в некоторой окрестности точки существуют обратные отображения и , и для системы уравнений (3) можно поставить в соответствие локально эквивалентную систему функциональных связей

определенную в окрестности точки из пространства , где , . Причем якобиан обратного отображения в точке не равен нулю.

Таким образом, система функций и в окрестности точки устанавливает взаимно-однозначное соответствие этой окрестности и множества точек, образованных значениями функций и , принимаемыми в данной окрестности.

На совокупности точек , где якобиан J равен нулю, уравнения (3) не определяют в окрестности точки переменные (a, κ) как неявные функции от (Q, M). Однако в этой точке существует единственное решение .

Вычислим компоненты матрицы Якоби (4), дифференцируя по параметрам состояния правые части уравнений равновесия (3). После преобразований имеем:

Введение в рассмотрение падающего участка диаграммы деформирования приводит к тому, что функция потенциальной энергии механической системы (1) имеет катастрофу типа сборки (или складки) [8] на пространстве допустимых управлений . Отсюда на всем пространстве можно обозначить область Ξ (), где отображение Φ не является взаимно-однозначным и любой точке из Ξ обратный оператор ставит в соответствие три пары параметров состояния балки (a, κ). Таким образом, имеет место локальный гомеоморфизм отображения Φ. Известно [7], что отображение гомеоморфно в некоторой точке пространства, если определитель матрицы Якоби (4) в этой точке не равен нулю. В задаче о чистом изгибе и растяжении это условие есть

(5)

Точки пространства , удовлетворяющие условию (5), являются критическими точками [8] отображения Φ. На плоскости параметров состояния совокупность критических точек образует линии критических отображений, разделяющие Ω на области, где матрица (4) либо положительно определена, либо отрицательно определена, либо не является знакоопределенной. Соответственно на этих областях функции и либо выпуклы вверх, либо выпуклы вниз, либо имеют седловые точки [9].

Отображение линий критических точек посредством уравнений равновесия (2) дает сепаратрису потенциальной функции (1). Она представляет собой проекцию крайних листов сборки на пространство допустимых управлений и поэтому ограничивает область Ξ. Отметим, что отсутствие глобального гомеоморфизма приводит к тому, что пространство допустимых управлений в результате отображения пространства состояний системы с помощью уравнений равновесия деформируется, зачастую сужаясь. Этот факт объясняется тем, что при отображении границы пространства (a = 0, κ = 0) не переходят в границы (Q = 0, M = 0).

3. Метод построения сепаратрисы потенциальной функции механической системы. Алгоритм построения сепаратрисы состоит из следующих этапов:

1) Выписывается матрица Якоби (6) для балки с заданной геометрией и свойствами материала, и определитель этой матрицы приравнивается нулю. На плоскости параметров состояния Ω отмечаются все точки, удовлетворяющие равенству (5). Для этого один из параметров состояния фиксируется, например, κ. Множество допустимых кривизн разбивается сеткой на N интервалов с малым шагом . Значение каждого узла сетки подставляется в уравнение (5), которое решается относительно отклонения a. Получаем соответствующую величину . Совокупность пар , образует на плоскости Ω кривую критических отображений оператора Φ. Возможно и построение критических точек и с помощью любого современного вычислительного пакета непосредственно из условия (5).

2) Полученные в п.1 величины ΘC подставляем в правые части уравнений равновесия (3) и, вычислив интегралы, находим соответствующие значения растягивающей силы и изгибающего момента . На плоскости допустимых управлений эти точки образуют сепаратрису потенциальной функции (1).

4. Устойчивость процесса деформирования балочного элемента. Для исследования устойчивости воспользуемся методами специальной математической теорией катастроф [8, 10], в соответствии с которой считаем, что при деформировании материал балки неотличим от нелинейно упругого и характеризуется потенциалом напряжений . Состояние всей системы описывает потенциальная функция (1).

Критические (морсовские) точки функции Π определяет равенство нулю градиента потенциальной функции [9], то есть необходимо выполнение уравнений

, ,

совпадающих со статическими уравнениями равновесия (2). Соотношения (2) связывают параметры управления и состояния системы в устойчивых и неустойчивых положениях равновесия балки. Для определения вырожденных критических точек, в которых происходит смена типов равновесия (с устойчивого на неустойчивое), выписывается матрица устойчивости (матрица Гессе) [10]

(6)

и совместно с уравнениями (2) решается уравнение

(7)

Компоненты симметричной матрицы (6) есть частные производные функций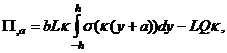

по параметрам состояния κ и a:

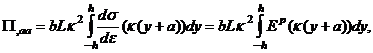
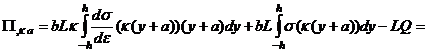
Очевидно, что матрица Гессе зависит не только от параметров состояния системы, но и от управлений Q. Тогда и равенство (7), имеющее вид

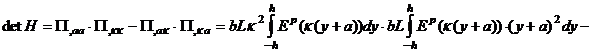
также есть уравнение относительно трех переменных (a, κ и Q). Однако для определения вырожденных критических точек решается система уравнений (2) и (7). Преобразуем (7) с учетом уравнений равновесия:

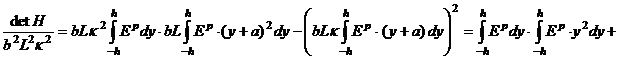
В начале процесса нагружения напряженно-деформированное состояние балки устойчивое. В каждой точке сечения и . При постепенном возрастании прикладываемой нагрузке согласно принципу максимального промедления [8] балка будет сохранять устойчивое равновесие до тех пор, пока определитель матрицы Гессе (гессиан) не обратится в нуль. В этот момент критическая точка, отвечающая данному положению равновесия, становится вырожденной и процесс нагружения скачкообразно теряет устойчивость. Потеря устойчивости процесса нагружения сопровождается разрушением материала балки микропорами и микротрещинами, нарушая сплошность среды. Таким образом, условие (7) можно рассматривать как критерий разрушения механической системы.

Отметим, что, несмотря на различие матриц Якоби и Гессе (первая несимметричная, вторая симметричная), их определители отличаются в раз и условия (5) и (7) приводят к одному уравнению относительно параметров состояния системы. Отсюда, вырождение матрицы Якоби (4) есть вырождение матрицы Гессе (6). Таким образом, возможно отождествить разрушение балочного элемента, потерю устойчивости процесса деформирования и вырожденность отображения пространства состояний в пространство управлений.

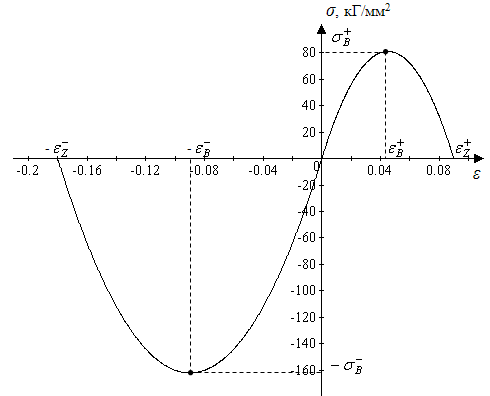
5. Пример расчета предельной несущей способности прямоугольной балки. Проиллюстрируем методику расчета предельной несущей способности для прямоугольной балки высотой 2h =10 мм, длиной L = 50 мм, шириной b = 1 ммрh. Свойства материала, из которого изготовлена балка, описывает непрерывная функция (рис. 3)

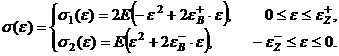(8)

Здесь - модуль Юнга, 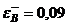, - деформации, отвечающие пределам прочности, , - деформации разрушения при сжатии и растяжении соответственно. На диаграмме т 162 кГ/мм2, 81 кГ/мм2 - напряжения предела прочности.

Для выбранной зависимости (8) функция касательного модуля имеет вид:

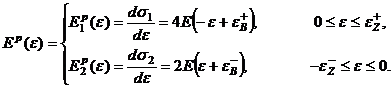
В точке значения касательного модуля функций σ1 и σ2 совпадают . Это обеспечивает гладкость функции σ(ε) в начале координат.

Потенциальная функция (1) для балки из материала с диаграммой (8) представляет собой катастрофу типа складки относительно параметров управления при заданном значении параметра κ = 0.01 мм-1 [8, 10] (рис. 4).

Граничные условия (3) после подстановке функции (8) представляют собой явную зависимость параметров управления и состояния:

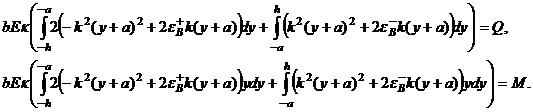(9)

Вычислим компоненты матрицы Гессе (6):

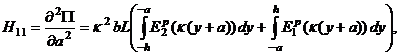
Из равенства нулю определителя матрицы Гессе det(H) = 0, которое в случае прямоугольной балки с учетом уравнений равновесия (9) представляет собой уравнение

, (10)

получаем совокупность критических точек отображения пространства состояний в пространство управлений (9). На плоскости Ω = {(a, κ): a ≥ 0, κ ≥ 0} эти точки образуют кривые Γ1 и Γ2 (рис. 5).

Отображая кривые Γ1 и Γ2 посредством уравнений равновесия (9) получаем сепаратрису потенциальной функции механической системы. Для этого проводится численная процедура, представленная в п. 3. Плоскость параметров состояния Ω разбивается прямоугольной сеткой с малым шагом. Далее один из параметров, например κ, фиксируется равным некоторому значению и уравнение (10) решается численно (итерационными методами Ньютона, простой итерации или др.) относительно параметра a с заданной степенью точности и соответствующим выбором начального приближения. В зависимости от начального приближения возможно определить все параметры состояния, удовлетворяющие (10).

Найденные значения (a,κ) подставляем в правые части уравнений (9), рассчитываем интегралы, и получаем соответствующие значения критических нагрузок (Q, M). Перебирая все точки на кривых Γ1 и Γ2, вычисляем точки сепаратрисы потенциальной функции системы (рис. 6). Причем Γ1 отображается в S1, часть Γ2 – в нижнюю полуплоскость пространства Q-M , оставшаяся часть кривой Γ2 после отображения оператором Φ переходит в множество S2. Отметим, что сепаратриса S1 – это проекция верхнего края сборки на плоскость Q-M (рис. 4). После достижения этой кривой S1 происходит “срыв” с верхнего листа сборки на нижний, что соответствует потери устойчивости процесса деформирования.

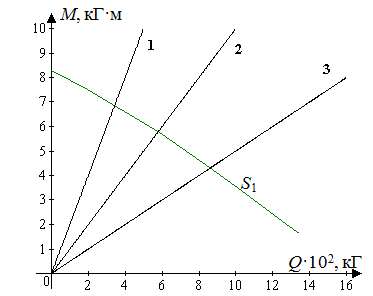В зависимости от способа нагружения системы, ее отклик на нагрузку разный. Рассмотрим несколько возможных зависимостей изгибающего момента M от растягивающей силы Q. Первый путь нагружения M =2Q (прямая 01 на (рис. 7)). Критическая нагрузка в этом случае есть точка пересечения прямой M =2Q и веткой сеператрисы S1. Для точного определения критической нагрузки заменяем во втором уравнении (2) M на 2Q и численно решаем систему нелинейных уравнений (2) и (10). Найденные решения уравнений представлены в таблице 1.

путь нагружения	растягивающее усилие Q, кГ	изгибающий момент M, кГ·мм	отклонение от нейтр. оси a, мм	кривизна κ, мм-1
01 (M=2Q)	343.22	6864.39	2.68467	0.0051453
02 (M=Q)	577.13	5771.32	3.9587	0.
03 (M=Q/2)	862.74	4313.7	6.03318	0.

Таблица 1.

Также были рассмотрены пути M = Q и M = Q/2 – прямые 02 и 03 на (рис. 7). Рассчитанные значения нагрузки и параметров состояния представлены в Таблице 1.

Заключение.

1) Проведено исследование устойчивости процесса деформирования балки прямоугольного сечения при чистом изгибе и растяжении. Получен критерий потери устойчивости.

2) Предложен метод построения сепаратрисы потенциальной функции механической системы.

3) Представлен пример расчета критических нагрузок балки с заданными свойствами материала.

Работа выполнена при финансовой поддержке РФФИ (проект № ) и частичной поддержке молодежного гранта УрО РАН (проект № 11-1-НП-523).

ЛИТЕРАТУРА

*****iping Guoa, Guangxin Lib. Elasto-plastic constitutive model for geotechnical materials with strain-softening behaviour // Computers & Geosciences. – 2008. – V. 34, № 1. – P. 14–23.

2. S. Tangaramvong, F. Tin-Loi. Limit analysis of strain softening steel frames under pure bending // Journal of Constructional Steel Research. – 2007. – V. 63, № 9. – P. 1151–1159.

3. M. Shazlya, V. Prakasha, Bradley A. Lerchb. High strain-rate behavior of ice under uniaxial compression // International Journal of Solids and Structures. – 2009. – V. 46, № 6. – P. 1499–1515.

4. Ильюшин . Ч.1. Упруго-пластические деформации - М.: Логос, 20с.

5. Работнов материалов. – М.: Физматгиз, 1962. – 456 с.

6. , Фомин теории функций и функционального анализа. – М.: Наука, 1972. – 496 с.

7. Зорич анализ. Ч.1. – М.: МЦНМО, 2002. – 664 с.

8. Gilmore R. Catastrophe Theory for Scientists and Engineers. - New York: Dover, 19p.; русск. пер.: Прикладная теория катастроф: В 2-х книгах; Кн. 1. - М.: Мир, 19c.

9. Матричный анализ. – М.: Мир, 1977. – 742 с.

10. Thompson J. M. T. Instabilities and catastrophes in science and engineering. – New York, 1982.: русск. пер.: Томпсон Дж. М. Т. Неустойчивости и катастрофы в науке и технике. - М.: Мир, 1985. – 254 с.