УДК 622.132.345:625
КИНЕТИКА И ИЕРАРХИЯ ПРОЦЕССА НАКОПЛЕНИЯ ТРЕЩИН В ГЕТЕРОГЕННЫХ МАТЕРИАЛАХ
д. ф.-м. н. , д. ф.-м. н. , к. ф.-м. н. ,
Физико-технический институт им. РАН, г. Санкт-Петербург, Россия
АННОТАЦИЯ: Приведены результаты исследований методом акустической эмиссии (АЭ) накопления трещин при сжатии гранитов. Установлено, что распределение трещин по размерам оптимизировано и представляет собой совокупность канонических термодинамических ансамблей. Число трещин в каждом ансамбле осциллирует со временем.
Исследования процесса накопления микротрещин [1–6] в напряженных твердых телах показали, что когда их концентрация ![]() в объеме тела достигает значения, при котором среднее расстояние между ними
в объеме тела достигает значения, при котором среднее расстояние между ними ![]() в
в ![]() раз больше их среднего размера
раз больше их среднего размера ![]() , т. е.
, т. е.
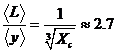 , (1)
, (1)
то формируется очаг разрушения. На этом основании в [1–3] была предложена двухстадийная модель разрушения. Предполагалось, что после приложения напряжений в теле начинают накапливаться микротрещины приблизительно одного размера. Когда их концентрация достигает порогового значения ![]() , возникают кластеры, в которых трещины начинают укрупняться, и образуется очаг, рост которого приводит к разрушению образца.
, возникают кластеры, в которых трещины начинают укрупняться, и образуется очаг, рост которого приводит к разрушению образца.
Однако, проведенный недавно анализ [4, 5] динамики плотности вероятности сигналов акустической эмиссии (АЭ) от нагруженных гранитов показал, что кинетика разрушения имеет более сложный характер. А именно, временная зависимость числа сигналов АЭ может быть разделена, по крайней мере, на четыре интервала, в которых амплитуда АЭ изменяется в противофазе. На этом основании была построена иерархическая модель разрушения горных пород. Предполагается, что первая стадия разрушения заключается в накоплении невзаимодействующих трещин первого ранга. Когда их концентрация в объеме тела достигнет критического значения ![]() , удовлетворяющего (1), трещины начинают укрупняться. В результате формируются трещины второго ранга. Эти трещины накапливаются до тех пор, пока их концентрация снова не достигнет критического значения
, удовлетворяющего (1), трещины начинают укрупняться. В результате формируются трещины второго ранга. Эти трещины накапливаются до тех пор, пока их концентрация снова не достигнет критического значения ![]() , что приводит к образованию трещин третьего ранга и т. д.
, что приводит к образованию трещин третьего ранга и т. д.
В работе с позиций статистической физики проведен анализ сигналов АЭ от гранитов. Идея применить подобный подход возникла в связи с результатами исследований эволюции дефектов нанометровых размеров на поверхности механически напряженных металлов [7–9]. Исследования показали, что их распределения представляют собой сумму канонических распределений Гиббса для флуктуаций энергии. На этом основании был сделан вывод, что нанодефекты образуют несколько статистических термодинамических ансамблей, распределение дефектов в каждом из которых термодинамически оптимизировано, т. е. задано условием, что конфигурационная энтропия имеет максимальное значение. Оказалось, что число нанодефектов в соседних ансамблях изменяется в противофазе. Эти изменения обусловлены тем, что когда число нанодефектов в каком-либо ансамбле достигает значения ![]() , их численная энтропия приобретает максимальное значение [7, 9]. По этой причине ансамбль теряет устойчивость и рассасывается с образованием более крупных нанодефектов следующего иерархического уровня.
, их численная энтропия приобретает максимальное значение [7, 9]. По этой причине ансамбль теряет устойчивость и рассасывается с образованием более крупных нанодефектов следующего иерархического уровня.
В этой связи эмпирическое условие (1) приобретает смысл второго начала термодинамики для случая дефектообразования в механически напряженных материалах.
Попытаемся ответить на следующие вопросы:
– по какой причине размеры микротрещин в гранитах варьируют в широких пределах;
– могут ли быть объяснены с позиций статистической механики обнаруженные ранее изменения амплитуды сигналов АЭ со временем.
Предполагалось, что, если будут получены положительные ответы на эти вопросы, откроется возможность обосновать иерархическую модель разрушения горных пород, предложенную в [4, 5], с позиций современной статистической физики.
Методика эксперимента детально рассмотрена в работах [3], поэтому остановимся только на ее схематическом описании. Цилиндрические образцы гранитов – «мелкозернистого» – Westerly и «крупнозернистого» – Harcourt – подвергали воздействию постоянного гидростатического давления и одноосного сжатия. Регистрация АЭ осуществлялась с временным разрешением ![]() с. База данных представляла собой хронологическую последовательность сигналов АЭ, амплитуда которых (А) была приведена к референс-сфере радиусом 10 мм. Эксперименты заканчивались в тот момент, когда начиналось резкое падение нагрузки, свидетельствующее о потере несущей способности образца.
с. База данных представляла собой хронологическую последовательность сигналов АЭ, амплитуда которых (А) была приведена к референс-сфере радиусом 10 мм. Эксперименты заканчивались в тот момент, когда начиналось резкое падение нагрузки, свидетельствующее о потере несущей способности образца.
Будем полагать, что амплитуда сигнала АЭ пропорциональна энергии образования микротрещин и для описания распределения амплитуд используем каноническое распределения Гиббса [11, 12] в следующем виде:
 , (2)
, (2)
где ![]() – число импульсов с амплитудой А;
– число импульсов с амплитудой А; ![]() – среднее значение амплитуды; n0 – нормировочная постоянная.
– среднее значение амплитуды; n0 – нормировочная постоянная.
Распределение (2) термодинамически оптимизировано, т. е. конфигурационная энтропия системы максимальна.
Если рассматриваемая система состоит из m статистических ансамблей, то распределение амплитуд должно представлять собой сумму выражений (2):
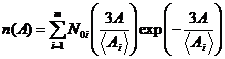 . (3)
. (3)
При описании реальных распределений амплитуд АЭ в (3) варьировали число распределений m и значения среднего размера ![]() . Чтобы уменьшить число подбираемых параметров, воспользовались результатами из работ [7–9, 13–15]. В [13] было показано, что энтропия идеальной смеси объектов максимальна, когда отношение их средних размеров равно трем. В [14, 15] установлено, что отношение средних размеров блоков в горных породах, геоблоков и мегаблоков составляет » 2–5. Наконец, в результате анализа распределений нанодефектов на поверхности металлов [7–9] было найдено, что отношение их средних размеров также равно трем.
. Чтобы уменьшить число подбираемых параметров, воспользовались результатами из работ [7–9, 13–15]. В [13] было показано, что энтропия идеальной смеси объектов максимальна, когда отношение их средних размеров равно трем. В [14, 15] установлено, что отношение средних размеров блоков в горных породах, геоблоков и мегаблоков составляет » 2–5. Наконец, в результате анализа распределений нанодефектов на поверхности металлов [7–9] было найдено, что отношение их средних размеров также равно трем.
Учитывая эти факты, полагали, что отношение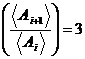 для соседних слагаемых в (3).
для соседних слагаемых в (3).
Затем добивались наилучшего совпадения рассчитанных и экспериментальных распределений за счет подбора ![]() и m.
и m.
Оказалось, что распределения квадратов амплитуд акустических сигналов для всех испытанных образцов гранитов хорошо описывается выражением (3) (рис. 1).
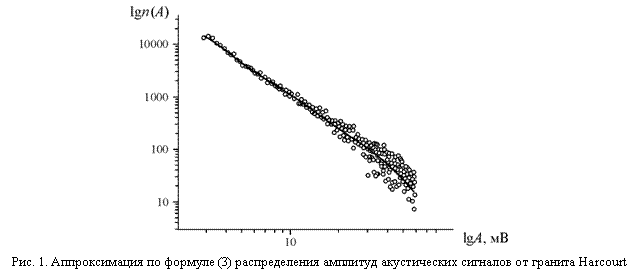 |
Число членов в сумме (3) для обоих гранитов составило 3.
Исследования, выполненные в последние годы, показали, что распределения различных объектов по размерам описываются каноническим распределением Гиббса. К ним относятся: нанодефекты и пятна коррозии на поверхности металлов [7–9, 16], разориентация дислокационных стенок в металлах [17, 18], структурные образования в полимерах [8, 19, 20], «островки» алюминия на поверхности полимерной пленки [20], агрегаты сажи в резине, бактерии, грибки и длины протеиновых молекул [8] и т. д.
Таким образом, возможность описания распределения микротрещин по размерам формулой (3) не является исключением. Как и все упомянутые объекты, микротрещины образуют совокупность статистических ансамблей, в которых их размеры термодинамически оптимизированы. Следовательно, существование широкого распределения размеров микротрещин есть следствие второго начала термодинамики.
Средние значения амплитуд сигналов АЭ ![]() для 1, 2 и 3 ансамблей приведены в таблице. Там же приведены значения интервала амплитуд
для 1, 2 и 3 ансамблей приведены в таблице. Там же приведены значения интервала амплитуд ![]() для каждого из иерархических уровней, найденные в [3–5]. Видно, что средние значения
для каждого из иерархических уровней, найденные в [3–5]. Видно, что средние значения ![]() попадают внутрь интервала
попадают внутрь интервала ![]() . Этот результат позволяет заключить, что найденные в [3–5] иерархические уровни соответствуют различным термодинамически оптимизированным ансамблям.
. Этот результат позволяет заключить, что найденные в [3–5] иерархические уровни соответствуют различным термодинамически оптимизированным ансамблям.
ТАБЛИЦА. Средние значения амплитуд, найденные в данной работе, и интервала амплитуд ![]() сигналов АЭ, установленные в [3–5], для каждого из статистических ансамблей
сигналов АЭ, установленные в [3–5], для каждого из статистических ансамблей
Westerly | Harcourt | ||||
№ ансамбля, п/п |
|
| № ансамбля, п. п. |
|
|
1 | 6.75 | 2.7–6 | 1 | 3.38 | 1.6–5 |
2 | 20.25 | 6–40 | 2 | 10.13 | 5–20 |
3 | 60.75 | 40–90 | 3 | 30.39 | 20–65 |
Чтобы исследовать эволюцию ансамблей микротрещин, были сделаны выборки с интервалом 1000 s. В каждом из них рассчитывали распределения амплитуд АЭ и описывали их выражением (3). Затем в каждом ансамбле строили зависимости числа амплитуд от времени.
На рис. 2 показана зависимость от времени числа микротрещин в ансамблях 2 – (![]() мВ) и 3 – (
мВ) и 3 – ( мВ) в граните Harcourt от времени. Видно, что, как и в [4, 5], число микротрещин в соседних ансамблях изменяется в противофазе.
мВ) в граните Harcourt от времени. Видно, что, как и в [4, 5], число микротрещин в соседних ансамблях изменяется в противофазе.
Такие же противофазные изменения числа микротрещин в соседних ансамблях наблюдались в граните Westerly.
 Изменения концентрации нанометровых дефектов в противофазе (размеры от 10 до 500онм) ранее наблюдалось также для поверхности нагруженных металлов [7, 9]. Следовательно, явление противофазного изменения их числа в соседних термодинамических ансамблях осуществляется в металлах и гранитах в интервале линейных размеров, » 5 порядков.
Изменения концентрации нанометровых дефектов в противофазе (размеры от 10 до 500онм) ранее наблюдалось также для поверхности нагруженных металлов [7, 9]. Следовательно, явление противофазного изменения их числа в соседних термодинамических ансамблях осуществляется в металлах и гранитах в интервале линейных размеров, » 5 порядков.
Таким образом, установлено, что распределение микротрещин по размерам термодинамически оптимизировано. Микротрещины формируют три статистических термодинамических ансамбля. Число микротрещин в соседних ансамблях изменяется в противофазе.
Работа выполнена при финансовой поддержке РФФИ, грант № .
СПИСОК ЛИТЕРАТУРЫ
1. Kuksenko V. S., Ryskin V. S., Betechtin V. I., Slutsker A. I. – 3Intern. J. Fracture Mech. – 1975. – Т. 11. – № 5.
2. Тамуж В. П., Куксенко разрушения полимерных материалов. – Рига: Зинатне, 1978.
3. Kuksenko V., Tomilin N., Damaskinskaja E., and Lockner D. Рuге Appl. Geophys. – 1996. – V. 146. – № 1.
4. Томилин Н. Г., Дамаскинская Е. Е., Куксенко В. С. // ФТТ. – 1994. – Т. 36. – № 10.
5. Томилин Н. Г., Куксенко модель разрушения горных пород. В сб. Науки о земле. Физика и механика материалов. – М.: Вузовская книга, 2002.
6. Петров В. А., Башкарев А. Я., Веттегрень основы прогнозирования разрушения конструкционных материалов. – СПб.: Политехника, 1993.
7. Килиан Х. Г., Веттегрень В. И., Светлов В. Н. // ФТТ. – 2000. – Т. 42. – 2001. – Т. 43.
8. Kilian H. G., Koepf M., Vettegren V. I. Prog. Colloid Polym. Sci. – 2001. – V. 117. – № 2.
9. Башкарев А. Я., Веттегрень В. И., Светлов В. Н. // ФТТ. – 2002. – Т. 44. – № 7.
10. Журков С. Н., Куксенко В. С., Петров В. А. и др. // Изв. АН СССР. Сер. Физика Земли. – 1977. – № 6.
11. Gibbs J. W. Elementary Principles in Statistical Mechanics. – Yale University Press: New Haven, CT, 1902.
12. Lavenda B. L. Statistical Physics. A Probabilistc Approach. – J. Wiley & Sons, Inc.: N. Y., 1997.
13. Kilian H. G., Metzler R., Zink B. J. Chem. Phys. – 1997. – V. 107. – № 12.
14. Садовский М. А. // Доклады АН СССР. – 1979. – V. 247. – № 4.
15. Садовский свойства геофизической среды. – М.: Наука, 1989.
16. Веттегрень В. И., Башкарев А. Я., Морозов Г. И. – Письма в ЖТФ. – 2002. – Т. 28. – № 13.
17. Miodownik M., Godfray A. W., Holm E. A., Hughes D. A. – Acta Mater, 1999. – V. 47. – № 9.
18. Hughes D. A., Liu Q., Hhrzan D. S., Hansen N. – Acta Mater, 1997. – V. 45. – № 1.
19. Бронников С. В., Суханова Т. Е., Лайус Л. А. – Высокомол. Соед. (A). – 2002. – V. 44. – № 6.
20. Bronnikov S. V., Sukhanova T. E. // Image analysis and steriology. – 2001. – V. 20. – № 1.
21. Веттегрень В. И., Бакулин Е. А., // ФТТ. – 2002. – V. 44. – № 4.
22. Журков С. Н., Куксенко В. С., Петров В. А. // Изв. АН СССР. Физика Земли. – 1977. – № 6.


 , мВ
, мВ