26 замечательных кубиков

Х региональное соревнование юных исследователей «Будущее Севера. ЮНИОР»

«Естественные науки и современный мир»: математика

26 ЗАМЕЧАТЕЛЬНЫХ КУБИКОВ

Автор:

МОУ Зверосовхозская СОШ, 6 класс

Научный руководитель:

МОУ Зверосовхозская СОШ, учитель

н. п. Зверосовхоз

2012

В детстве мне очень нравилось рассматривать узоры, возникающие в зеркальном калейдоскопе. Один поворот игрушки и узор меняется до неузнаваемости. Когда мне в руки впервые попал кубик Рубика, я просто рассматривала узоры, возникающие на его гранях вследствие хаотичных поворотов. Но вернуть кубик в первоначальное состояние даже не помышляла.

В этом году кубик Рубика появился у нас в классе. Учитель математики предложила нам собрать одну грань. Мне казалось, что это простая задача, но с первой попытки ничего не получилось. Оказалось, что и все мои одноклассники не могут справиться с этой задачей. И тогда у нас возникла идея – надо не просто научиться собирать одну грань, а познакомиться с этой головоломкой поближе.

На занятиях математического кружка мы познакомились с историей кубика Рубика, рассмотрели различные схемы сборки кубика, попробовали собирать кубик используя различные инструкции. Есть схемы, требующие осмысления ситуации, сложившейся на гранях кубика – такие схемы более сложные и я могу пока пройти лишь 2-3 шага из 9, т. е. собрать два слоя кубика. Но я думаю, что постепенно научусь собирать кубик полностью.

Наблюдая за тем, как изменяет свои положения кубик, я задалась вопросом, - а сколько всего положений есть у этой головоломки и из каждого ли положения можно собрать кубик Рубика. Я решила провести исследование по этой теме.

Цель исследования: вычислить количество возможных положений кубика и выяснить из любого ли положения можно выполнить сборку двух его слоёв.

Для достижения цели исследования были поставлены следующие задачи:

1) изучить литературные источники по решению комбинаторных задач;

2) изучить послойную схему сборки кубика Рубика;

3) исследовать количество положений головоломки;

4) создание схемы сборки одной грани кубика путём систематизации возможных положений граней кубика;

5) распространить опыт работы со схемой среди одноклассников.

Вычисление количества положений кубика Рубика.

Поверхность кубика Рубика состоит из 6 граней шести цветов. Каждая грань состоит из 9 квадратов, т. е. всего на поверхности кубика 54 квадрата, каждый из которых может быть окрашен в один из шести цветов: красный, оранжевый, жёлтый, белый, синий, зелёный.

Чтобы вычислить количество положений кубика Рубика найдём общее количество вариантов окраски 54 квадратов в шесть различных цветов.

Первый квадрат может быть окрашен одним из 6 цветов. Для каждого цвета первого квадрата возможны 6 вариантов окраски второго квадрата, т. е. имеем 6х6 вариантов окраски двух квадратов. Из каждого способа окраски двух первых квадратов имеем по 6 вариантов окраски третьего квадрата. Всего получаем 6х6х6 вариантов окраски трёх квадратов. Таким образом, при рассмотрении каждого следующего квадрата число возможных окрасок рассматриваемых квадратов увеличивается в 6 раз. Значит 54 квадрата могут быть окрашены шестью цветами 654 способами.

Решение задачи оказалось достаточно простым: количество положений кубика 654.

Изучая литературу, связанную с кубиком Рубика я постоянно обращала внимание, что квадраты кубика не окрашены произвольно. Рассмотрев строение кубика я увидела, что центральные квадраты жёстко закреплены на крестовине и если не менять положение крестовины при вращении кубика, т. е. чётко определить верхнюю-нижнюю, правую-левую, переднюю-заднюю грани, то получается, что центральные квадраты не меняют свой цвет: если верхний центральный квадрат – зелёный, то нижний – обязательно синий; а в боковых гранях белый центральный квадрат всегда расположен напротив жёлтого, а красный напротив оранжевого.

Проведя все эти рассуждения понятно, что вывод о количестве положений кубика Рубика является преждевременным, т. к. совершенно не учитывает устройство кубика.

Разделим кубики, составляющие поверхность кубика Рубика, на центровые (закреплённые на крестовине), угловые и рёберные. Центровые имеют только одну окрашенную грань и они не меняют своего положения, т. е. при решении нашей задачи мы не будем брать их в расчет.

Угловых кубиков – восемь. Угловые кубики имеют по три окрашенных грани, т. е. каждый кубик может располагаться на одном и том же месте тремя разными способами, а все восемь угловых кубиков N = 38 способами.

Надо вычислить количество перестановок восьми кубиков в восьми углах. Первый кубик может быть поставлен в любой из 8 углов, второй – в любой из 7 оставшихся и т. д. Количество перестановок будет равно P8 = 8·7·6·5·4·3·2·1 = 8! Используя правило умножения (основное правило комбинаторики) получим количество положений угловых кубиков, равное произведению N·P8 = 38·8! = 264 539 520.

Рассмотрим теперь рёберные кубики. Каждый из них имеет 2 окрашенные грани, количество рёберных кубиков – 12. Аналогично рассуждая, получим, что количество положений рёберных кубиков равно произведению N·P12 = 212·12! = 1  600.

Основываясь на правиле умножения, имеем, что количество возможных положений рёберных и угловых кубиков равно (38·8!) · (212·12!) =  000 (около 519 квинтиллионов!).

Схема сборки одной грани кубика Рубика.

Несмотря на огромное количество положений на гранях кубика каждый раз можно провести систематизацию этих положений и найти алгоритм решения для каждой ситуации. В результате такой систематизации появляется схема сборки кубика Рубика.

Я хочу предложить схему сборки одной грани, по которой ученики 4-6 классов смогут собрать одну грань кубика Рубика, а также разобраться с основными обозначениями, применяемыми при записи алгоритма полной сборки.

Основные обозначения:

В – верхняя грань,

Н – нижняя грань,

П – правя грань,

Л – левая грань,

Ф – передняя (фронтальная) грань,

З – задняя грань.

Повороты:

В – поворот верхней грани по часовой стрелке,

В’ – поворот верхней грани против часовой стрелки,

В” – двойной поворот верхней грани (выполняется в любую сторону).

Введём также обозначения для средних слоёв:

Сг – средний горизонтальный слой,

Св – средний вертикальный слой.

1 шаг.

Определяем цвет грани, которую будем собирать, например – синий. Фиксируем центральный синий квадрат в верхней грани.

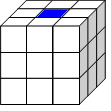
2 шаг.

Собираем в верхней грани все квадраты, которые можно поставить на место 1-2 поворотами.

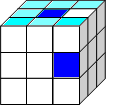
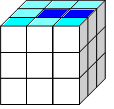
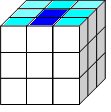
3 шаг.

Собираем рёберные кубики.

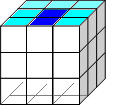
4 шаг.

Собираем угловые кубики.

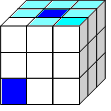
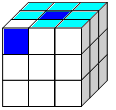
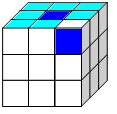
Для популяризации кубика Рубика среди моих сверстников:

ü  оформлена памятка-схема сборки одной грани кубика Рубика для учащихся 4-6 классов;

ü  в рамках работы математического кружка в кабинете математики оформлен стенд «Кубик Рубика» (см. Приложение ), где изложена информация об истории кубика Рубика, его строении;

ü  проведено соревнование по скоростной сборке одной грани кубика Рубика среди учащихся 5-6 классов (см. Приложение ).

В результате проведённой работы можно сделать следующие выводы:

1) решена задача вычисления количества положений кубика Рубика;

2) создана схема сборки одной грани с использованием общепринятых обозначений;

3) создана памятка-схема для распространения опыта по сборке кубика.

Используемая литература

1. , , Шварцбурд  5 класс. – М.: Мнемозина, 2008.

2. , , Шварцбурд  6 класс. – М.: Мнемозина, 2009.

3. Всем кубикам кубик // «Юный техник», 1982, № 2.

4. История кубика Рубика [Электронный ресурс]. – Режим доступа: http://www. *****/history/history. html.

5. Как собрать кубик Рубика [Электронный ресурс]. – Режим доступа: http://kak-sobrat-kubik-rubika. *****/.

6. Когда и как Эрно Рубик изобрёл кубик Рубика [Электронный ресурс]. – Режим доступа: http://*****/club/history/rubiks_cube/.

Приложение

Стенгазета «Кубик Рубика»

Приложение

Соревнование по скоростной сборке одной грани кубика Рубика

РЕЗУЛЬТАТЫ

соревнований по скоростной сборке одной грани кубика Рубика