Изучение свойств треугольников, вписанных в параболу

Научно-практическая конференция учащихся и педагогов

«Первые шаги в науку»

Изучение свойств треугольников, вписанных в параболу

Выполнил:

ученик 11 класса

ГУО«Речицкий районный лицей»

Научный руководитель –

учитель математики

ГУО«Речицкий районный лицей»

Брянск, 2013

Содержание

Введение…………………………………………………………………………3

1. Парабола в алгебре…………………………………………………………...4

2. Парабола и аналитическая геометрия……………………………………....6

3. Парабола и треугольник……………………………………………………...8

4. Об одном свойстве параболы………………………………………………..11

5. Интересные задачи…………………………………………………………...12

Заключение……………………………………………………………………....17

Литература……………………………………………………………………….17

Введение

В школьной программе заметное место уделяется построению графиков функций. Моя работа посвящена изучению параболы. Я думаю, она будет интересна и поучительна всем тем, кто увлечен таким предметом, как математика. Линию такую как парабола, мы изучали в 8 классе. В курсе аналитической геометрии, она имеет другую формулу и график. Свойства, которые я буду исследовать, найдут применение в различных предметах. Исследование начинается с элементарных фактов и заканчивается весьма удивительными вещами. В своей работе я буду наблюдать за параболой, около которой будет описан или в которую вписан треугольник. А также рассмотрю интересные задачи олимпиадного уровня. В основном упор будет делаться на задачи с треугольниками, так как там можно увидеть интересные вещи, которые могут быть исследованы в других работах. Тема моей исследовательской работы актуальна и может быть полезна школьникам старших классов, учителям, а также учащимся физико-математического направления, и просто тем, кто увлечен математикой.

1. Парабола в алгебре

Парабола – это график квадратичной функции вида y=ax2+bx+c. Ее также можно представить видом . Координаты вершины

(m, n) ее можно определить:, . Направление ветвей на графике зависит от коэффициента а, если a>0, то ветви направлены вверх, а если a < 0, то вниз.

Задача 1.Построить график функции y=x2

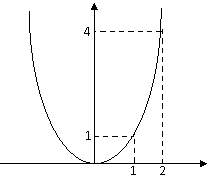Задача 2.Построить график функции y=(x+1)2

Задача 3.Построить график функции y=x2-1

Задача 4. Постройте график функции y=х² - 6х + 5

Найдем нули функции. x1=1, x2 =5. Найдем вершину: хв.=3, ув.= - 4.

2. Парабола и аналитическая геометрия

Парабола — геометрическое место точек, равноудалённых от данной прямой (называемой директрисой параболы) и данной точки (называемой фокусом параболы). Каноническое уравнение параболы в прямоугольной системе координат: .

Парабола является коническим сечением.

Задача 1. Составить уравнение параболы, вершина которой находится в начале координат, зная, что парабола расположена симметрично относительно оси Ох и проходит через точку А(9; 6)

Решение. Зная каноническое уравнение параболы y2=2ax, подставим в него координаты точки А. Формула будет выглядеть как 36=18a Откуда, а=2. Отсюда выводим уравнение параболы, которое будет y2=4x .

Задача2. Вывести условие, при котором прямая y=kx+b касается параболы y2=2px.

Решение.

Задача 3. Доказать, что к параболе y2=2px можно провести одну и только одну касательную с угловым коэффициентом равным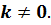

В задаче описанной выше было выяснено, что для касательной касающейся параболы, соблюдается условие p=2kb, где p – параметр определяющий параболу, а k и b – параметры, определяющие касательную. Но если заданы p и k, отсюда однозначно определяется , то касательная, существующая для данной прямой, имеющей k, и парабола, характеризующая параметром p единственна и оно однозначно k и b.

3.  Парабола и треугольник

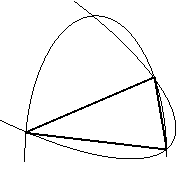
Свойства парабол и треугольников:

1)  Гипотенузы всех вписанных в параболу прямоугольных треугольников с фиксированной вершиной прямого угла проходят через одну и ту же точку.

2)  Площади вписанного и описанного вокруг параболы треугольников относятся как 2:1. .

3)  Для описанного треугольника АВС с точками касания с параболой P, M, Q выполняется соотношение: .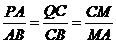

Задача 1. Касательные к параболе в точках 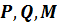образуют треугольник АВС. Доказать, что SPQM=2SABC

Решение.

Можно считать, что парабола задается уравнением x2=4y. В таком случае точки P, Q, M имеют координаты (2ti, ti2), где i=1, 2, 3. Легко проверить, что:

Решая данные определители, получим:

Как видим формулы получились аналогичные, что доказывает SPQM=2SABC

Задача 2. Докажите, что прямоугольный треугольник можно вписать в параболу y=x2 так, чтобы его гипотенуза была параллельна оси абсцисс, тогда и только тогда, когда его высота, опущенная из вершины прямого угла, равна единице.

Решение.

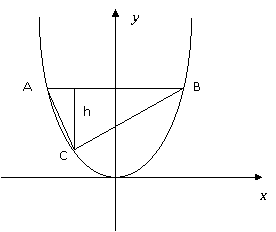А) Пусть в вписаный в параболу. Пусть а – абсцисса А, тогда -а – абсцисса точки В. А с – абсцисса точки С.

То точки А(а, а2), В(-а, а2), С(с, с2), то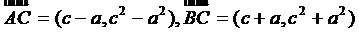

Условие перпендикулярности векторов

и равносильно равенству нулю их скалярного произведения. При этом , и. Поэтому:

Б) Доказать, что любой прямоугольный треугольник, у которого высота, опущенная на гипотенузу, равна 1, можно вписать в параболу y=x2 требуемым образом.

Пусть в прямоугольном треугольнике АВС гипотенуза АВ = u, а высота, опущенная на гипотенузу равна h=1. Очевидно, что u ≥ 2h = 2. Рассмотрим треугольник A1B1C1, у которого Очевидно, что все три эти точки лежат на параболе y=x2. Кроме того, тривиальная проверка показывает, что А1В1 = u; A1B12 = A1C12 + B1C12; h1 = 1, где h1–длина высоты, опущенной на вершины C1 на сторону A1B1. Следовательно, А1В1С1 – прямоугольный треугольник, у которого гипотенуза А1В1 равно гипотенузе прямоугольного треугольника АВС и высота h1 равна высоте h. Но это означает, что треугольники А1В1С1 и АВС равны, что и доказывает требуемое утверждение.

4.  Об одном свойстве параболы

Задача 1. На параболе у = ах2 рассмотрим три точки A, В, С, проекции которых на ось Оx равноотстоят друг от друга: |A1B1|=|B1C1|=m. Найдем площадь треугольника АВС.

Решение.

Для этого обозначим через x1, x2, x3 абсциссы точек А, В, С соответственно. По условию x2=x1+m, x3=x1+2m. Трапеция А1АСС1 составлена из треугольника АВС и двух трапеций А1АВВ1 и В1ВСС1 поэтому: Оказалось, что искомая площадь не зависит от абсциссы точки А, а только от расстояния m между соседними точками и от параметра а, определяющего крутизну параболы. Рассмотрим теперь общий случай – пусть абсциссы x1, x2, x3 точек АВС произвольны. Если x1<x2<x3, то можно рассуждать точно так же, как в предыдущем случае. Получаем формулу:

После преобразований получаем формулу:

Эта формула показывает, что площадь треугольника с вершинами на фиксированной параболе зависит только от разностей абсцисс его вершин. Когда треугольник скользит по параболе, изменяя свою форму, но сохраняя неизменными разности между абсциссами вершин, его площадь не меняется. Оказывается, что таким свойством обладает только парабола.

5.  Интересные задачи

Задача 1. На координатной плоскости нарисовали 2008 графиков квадратных трехчленов. Может ли оказаться, что для каждого из них существует прямая, имеющая общие точки с любым графиком, кроме него?

Решение.

Приведем пример бесконечного множества парабол Р1,Р2,Р3.., удовлетворяющих условию. Рассмотрим параболу Р, заданную уравнением y= - x2, и пусть парабола Рn симметрична параболе Р относительно точки Кn c координатами (n,- n2), n=1, 2… Каждая из парабол Рn имеет общую касательную ln с параболой Р. Парабола Рn лежит выше прямой ln и имеет с ней единственную общую точку Kn. Парабола Р лежит ниже прямой ln, в частности, все точки касания Ki, i ≠ n, лежат строго ниже прямой ln. Сдвинув немного вниз прямую ln, получим такую прямую ln’, что все точки Ki, i≠n, по-прежнему лежат строго ниже нее, а точка Kn–строго выше нее. Тогда прямая ln’ не пересекает только одну параболу Pn из множестваР1, Р2, Р3…

Задача 2. Доказать, что касательная к параболе y=x2 в точке М (х0,х02) имеет уравнение y=2x0x – x02. Этим будет доказано, что для каждого углового коэффициента k существует единственная касательная к параболе y=x2c угловым коэффициентом k – таковой будет касательная в точке , и только она.

Решение

1 доказательство.

Касательная к параболе в точке M(х0,х02) – это предельное положение прямой М1, М2, где М1(х0-έ,(х0-έ)2 при έ → 0. Вычислим угловой коэффициент k’ прямой М1, М2.

Значит и касательная к параболе в точке M имеет угловой коэффициент 2х0. Подбираем свободный член b уравнения y=2x0x+b так, чтобы касательная проходила через точку M(x0,x02). Имеем: х02=2х0х+b, откуда b = - x02.

2 доказательство

Уравнение касательной к графику функции y=f(x) в точке (x0,y0) выглядит как

и поскольку (x2)=2x, то уравнение касательной превращается в y=2x0x-x02.

3 доказательство

Для 3 способа будем использовать геометрическое определение параболы. Для параболы y=x2 фокус – это точка F , а директриса имеет уравнение . Докажем утверждение, называемое оптическим свойством параболы, а именно, что касательная к параболе в точке M является биссектрисой угла FMG (G — основание перпендикуляра, опущенного из точки M на директрису). Предположим, что биссектриса угла FMG не является касательной и имеет (кроме M) ещё одну точку пересечения с параболой, обозначим её буквой N. Опустим из N перпендикуляр NH на директрису. Поскольку точка M лежит на параболе, то FM=MG, значит, MN — биссектриса равностороннего треугольника FMG, а значит, и высота, и медиана. Другими словами, MN является серединным перпендикуляром к FG, следовательно, FN=NG. Кроме того, поскольку точка N лежит на параболе, то для неё верно равенство FN=NH. Мы получили противоречие: перпендикуляр NH не может быть равен наклонному отрезку NG, значит, биссектриса угла FMG имеет единственную общую точку с параболой (точку M), и, тем самым, является касательной. Заметим, что мы также доказали, что касательная к параболе в точке M (х0,х02) проходит через середину отрезка FG. имеющую координаты . Теперь, зная координаты уже двух точек, лежащих на касательной, несложно написать её уравнение.

Задача 3.А и В – некоторые точки на параболе, С – точка пересечения касательных к параболе в точках А и В. По точкам А, В и С постройте ось симметрии параболы.

Решение

Проведем оси так, чтоб вершина параболы находилась в начале координат, а ось Оу совпала с осью симметрии параболы. Уравнение касательных к параболе в точке (х0, у0):

Рассматривая точку С как точку пересечения двух касательных, получаем:

Отсюда следует, что 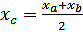. Значит, прямая СМ, где М – середина АВ, параллельна оси Оу. Теперь достаточно найти одну точку на оси Оу, чтобы задача была решена: проведя из этой точки прямую параллельную СМ мы получим ось Оу. Проведем прямые AE || BD || Ox. Координаты точек D и Е:

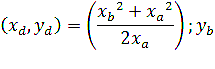
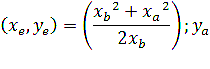
Докажем, что АВ и DE пересекаются на оси Оу.

Уравнение прямой АВ: . Координата y(1) пересечения прямой AB и Оу:

Уравнение прямое DE: 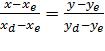. Координата у(2) пересечения DE c Oy:

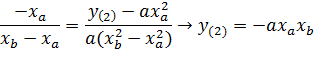
Следовательно, АВ и DE пересекают Оу в одной точке.

2 способ.

Вос­пользуемся таким фактом: пучок параллельных оси Оy прямых, отраженных от параболы, пересекается в фокусе параболы - точке на оси симметрии. Поскольку АС и ВС - касательные, мы легко можем построить отражения этих прямых от параболы в точках А и В. Проведём через точки А и В прямые l1, и l2, параллельные СМ. Пересечение отражений этих прямых лежит на оси Oy.

Заключение.

Моя работа интересна. Суть работы состоит в том, что здесь пересекается 2 раздела математики: алгебра и геометрия. Алгебра дает нам понятие о параболе и что она из себя представляет. С этим понятием мы давно знакомы, еще с 8 класса. Потом позже, уже в высшей математике мы перенесли ее в геометрию, где она получила свое новое имя и свойства. Я рассмотрел интересные случаи задач, которые, на мой взгляд, имеют среднюю сложность, и которые дают нам полное понятие о параболе. Задачи, дали мне еще несколько тем, над которыми можно подумать и взять как тему исследовательской работы. Парабола даем нам более легкий способ решения различных задач. Не зря один философ говорил, что геометрический метод хорош тем, что мы не допустим множества ошибок в длинных вычислениях. И он был прав, можно заметить, какими короткими получились вычисления. Я считаю, что работа поможет многим ученикам школ в решении различных задач, а также поступающим. К тому же, в физике такой способ есть и им мы довольно часто пользуемся, ведь он один из самых легких и популярных. Работа демонстрирует преимущества геометрических методов, сочетающих наглядность и логическую прозрачность. Задачи, которые были изложены тренируют геометрическое мышление и интуицию.

Литература:

1.  Парабола, Квант, № 4, 1975.

2.  , Об одном свойстве параболы, Квант, № 4, 1984.

3.  , Геометрические свойства кривых второго порядка. Москва, Издательство МЦНМО, 2007 год.

4.  "Сборник задач по аналитической геометрии". М., Наука, Физматлит, 1998.