Задача о ближайшем соседе
Дано: функция f (x, y) ³ 0 — затраты на обслуживание отрезка дороги
от x до y, 0 £ x £ y £ M, x, y — целочисленные точки,
n — число отрезков.
Найти: оптимальное разбиение сегмента [0,M] на n отрезков.
Математическая модель:
0 = x0 £ … £ xn = M
Алгоритм динамического программирования
Sk(y) — минимальные затраты на обслуживание k отрезков для сегмента [0, y].
Рекуррентные соотношения:
S1(y) = f (0,y), y = 1,…, M
, y = 1,…, M, k = 2,…, n.
T = O(nM 2) П = O(nM)
Оптимизация числа отрезков
Для каждого n = 1,…, M найти Sn(M) и выбрать наименьшее значение
T = O(M 3), П = O(M 2).
Модифицированный вариант
— минимальные затраты на обслуживание сегмента [0, y].
Рекуррентные соотношения:
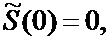
, y = 1,…, M.
T = O(M 2), П = O(M).
Задача замены оборудования
Приведение затрат к начальному моменту
Пусть c — банковский процент, или коэффициент эффективности капиталовложений (годовая норма дисконта
).
Если S1 — капитал в начальный год, то по истечении года эта сумма станет равной S2 = S1×(1 + c), а в конце t-го года St = S1×(1 + c)t–1.
Если в год t хотим потратить сумму St, то в начальный год должны иметь 
. Затраты St в год t, будучи приведенными к начальному моменту t =1, равны
где 
— коэффициент дисконтирования, 0 < a £ 1.
Если в течении T лет производились траты S1, S2,…, St то суммарные
приведенные затраты вычисляются по формуле:
Пример Рассмотрим распределение капитала в 8 млн. руб. в течение 8 лет при банковском проценте c = 0.1 (a = 0.91) и трех стратегиях:
1) все траты в 1-й год;
2) равномерные траты;
3) все траты в последний год.
Стратегия | Год | Суммарные |
1 | 8 – – – – – – – | 8.0 |
2 | 5.9 | |
3 | – – – – – – – 8 | 4.2 |
Постановка задачи
g — начальная стоимость оборудования;
ct — стоимость эксплуатации оборудования в t год, ct+1 ³ ct;
Система функционирует бесконечно, оборудование периодически заменяется.
T — период замены оборудования;
ST — суммарные затраты при фиксированном периоде замены T :
.
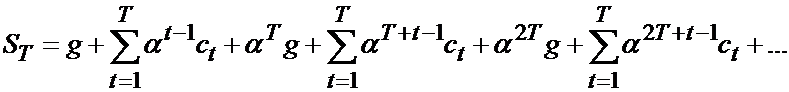за первые T лет за вторые T лет ………….
Благодаря дисконтированию затрат (a < 1) величина ST конечна:
.
Задача отыскания оптимального периода замены оборудования: 
Применение динамического программирования
Рассмотрим систему, функционирующую в течение T лет, причем решение о замене оборудования принимается каждый год.
Дано: {1,…, m} — набор типов оборудования;
— стоимость оборудования i-го типа, купленного в год t;
— стоимость годовых эксплуатационных затрат на оборудование i-го типа, купленного в год t и проработавшего t лет;
— остаточная стоимость оборудования i-го типа возраста t,
купленного в год t;
n — максимально допустимый возраст оборудования;
i0, t0 — тип и возраст оборудования в начале функционирования;
Пусть 
— минимальные суммарные затраты в интервале [t, T], приведенные к началу t-го года, при условии, что в начале t-го года было оборудование типа i возраста t. Требуется найти 
.
Рекуррентные соотношения:
| если замены нет, |
в случае замены, |
1 £ t £ n, 1 £ i £ m,
| если продолжаем эксплуатировать оборудование |
если заменяем оборудование |
1 £ t £ n, 1 £ i £ m, 1 £ t < T.
Алгоритм может быть реализован с трудоемкостью T = O(m2nT), и памятью П = O(mnT).
Вопросы
· e-аппроксимационная схема является полностью полиномиальной, если ее трудоемкость полиномиально зависит от e и от длины записи исходных
данных (Да или Нет)?
· Для любой задачи комбинаторной оптимизации можно построить полиномиальную аппроксимационную схему (Да или Нет)?
· Для задачи замены оборудования метод динамического программирования дает точное решение с полиномиальной трудоемкость (Да или Нет)?
