Определение момента инерции маховика

Работа № 6

Определение момента инерции маховика

Цель: определить момент инерции маховика, применить теорему Штейнера.

Оборудование: специальная установка, груз, штангенциркуль, секундомер.

Введение

Рассмотрим неизменяемую систему материальных точек (абсолютно твердое тело). Центром масс или центром инерции системы материальных точек называется такая воображаемая точка , радиус вектор которой выражается через радиус-векторы материальных точек по формуле

. (1)

Мерой инерции такой системы при поступательном движении является общая масса всей системы . Мерой инерции системы при вращательном движении служит величина

, (2)

которая называется моментом инерции. Эта величина зависит от расположения частей тела относительно оси вращения.

Пусть – момент инерции системы относительно оси, проходящей через центр масс . Найдем – момент инерции системы относительно параллельной оси, проходящей через точку (оси перпендикулярны плоскости рис. 1). Обозначим через – расстояние между осями. Тогда

.

Первое слагаемое представляет собой момент инерции относительно прежней оси, проходящей через точку , во втором слагаемом сумма равна нулю, т. к. прежняя ось проходи через центр масс и , сумма в третьем слагаемом равна массе всей системы . Получаем

(3)

– математическую формулировку теоремы Гюйгенса–Штейнера: момент инерции системы материальных точек (тела) относительно какой-либо оси равен моменту инерции относительно параллельной оси, проходящей через центр инерции, сложенному с величиной , где – расстояние между осями, а – масса всей системы.

Если вещество в теле распределено непрерывно, то вычисление момента инерции сводится к вычислению интеграла

, (4)

в котором – это расстояние от оси вращения до элемента массы .

При вычислении моментов инерции однородных тел простой формы относительно оси симметрии, проходящей через центр масс получается результат, который может быть представлен в виде:

,

где – коэффициент пропорциональности, зависящий от формы тела и выбора оси, – масса тела, – характерный размер тела (радиус, ширина, длина и т. д.) или характерное расстояние от части тела до оси. Например, для однородного диска или цилиндра – , для кольца , для однородного шара , где – радиус тела.

Описание установки

Маховик 1 в виде диска с резьбовыми отверстиями насажен на ось (рис. 2) и может вращаться с малым трением. На той же оси находится шкив 2 радиусом , на который наматывается нить. К другому концу нити привязан груз 4 массой , под действием которого система приводится во вращение. Путь , пройденный грузом до своего нижнего положения (когда нить полностью размотается), определяется по шкале 3, вдоль которой груз движется.

В резьбовые отверстия диска могут вворачиваться дополнительные грузы 5 цилиндрической формы радиуса и массы .

В установке предусмотрено автоматическое измерение времени движения груза до нижней точки и расстояния , на которое поднимается груз по инерции после прохождения нижнего положения.

Описание метода измерений

Если намотать нить на шкив, подняв груз на высоту , то он будет обладать потенциальной энергией . При падении груза его потенциальная энергия переходит в кинетическую энергию поступательного движения груза 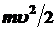, энергию вращения диска и работу по преодолению момента сил трения . Зная время падения груза до нижней точки, можно определить конечную скорость движения груза и угловую скорость вращения диска , где – радиус шкива.

При движении в подшипниках действует момент сил трения , для преодоления которого на пути , совершается работа

, (5)

где – угол поворота диска (угловое перемещение).

Работа сил трения равна изменению механической энергии системы

. (6)

В соответствии с законом сохранения энергии и равенством (5)

. (7)

Момент сил трения находится из следующих соображений. После того, как груз опустится до нижней точки, маховик, продолжая вращение по инерции, поднимет груз на высоту ; там его потенциальная энергия меньше, чем начальная, на величину работы, совершенной против сил трения на всём пути. Из закона сохранения энергии и формулы (2) следует

. (8)

Решая совместно уравнения (7) и (8), получим расчётную формулу для момента инерции вращающегося тела:

. (9)*

Следовательно, для определения момента инерции маховика, необходимо знать его массу , выбрать шкив и измерить его радиус , а также выбрать – начальную высоту, которой начинает двигать груз. Измеряя время движения груза до нижней точки и высоту , на которую поднимется груз при вращении маятника по инерции, по формуле (9) найдем – момент инерции маховика. Для уменьшения погрешности, вызванной случайными факторами, эксперимент необходимо повторить несколько раз, используя для вычисления средние значения измеряемых величин.

Выполнение работы

Задание 1. Определение момента инерции диска

1. Снять дополнительные грузы с диска.

2. Измерить штангенциркулем радиус шкива , радиус диска , радиус кольца и записать их в табл. 1.

3. Определить массу груза , подвешенного к нити и записать ее в таблицу. Массы диска и кольца указаны на установке.

4. Присоединить груз к нити, отметив на шкале его нижнее положение.

5. Включить питание на установке кнопкой с обратной стороны секундомера, вращая диск, намотать нить в один слой на шкив. Включить электромагнит красной кнопкой, расположенной в верхней части установки, зафиксировав положение маховика. Измерить и записать расстояние от груза до нижней точки.

Таблица 1

6. Нажать кнопку «Пуск». В момент прохождения грузом нижнего положения секундомер выключается. Продолжая дальше наблюдение за движением груза , заметить высоту , на которую поднимется груз, двигаясь по инерции. Показание секундомера и высоту записать в табл. 1.

7. Повторить измерения еще четыре раза при тех же значениях , и .

8. Вычислить экспериментальное значение момента инерции маховика по формуле (9), подставив в нее средние значения и .

9. Оценить теоретическое значение момента инерции маховика, состоящего из диска радиусом и массой и кольца радиусом и массой , по формуле

.

10. Сравнить полученные результаты и сделать вывод.

Задание 2. Применение теоремы Гюйгенса–Штейнера

1. Определить массу и радиус дополнительных грузов. Закрепить их на одинаковом минимальном расстоянии от оси вращения на диске установки и произвести измерение расстояния от оси вращения до центра грузов. Результаты этих измерений занести в табл. 2.

2. Занести в табл. 2 результаты измерений, полученных в задании 1: радиус шкива , массу груза , расстояние, проходимое грузом до нулевой отметки , а также записать число дополнительных грузов .

3. Провести измерения (см. п. п. 6–7 задания 1) и результаты занести в табл. 2.

4. Рассчитать момент инерции маховика с дополнительными грузами (формула 9).

Примечание:

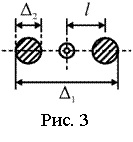Если прямые измерения расстояния от оси до центра дополнительных грузов затруднены, то можно провести измерения в несколько приемов. С помощью штангенциркуля определить расстояние между кромками дополнительных грузов (см. рис. 3) и диаметр дополнительного груза , тогда

.

Таблица 2

5. Рассчитать момент инерции системы «диск–дополнительные грузы», используя теорему Гюйгенса–Штейнера

,

и результат занести в табл. 2.

6. Провести подобные измерения и расчеты с тремя другими положениями дополнительных грузов на диске.

7. Нарисовать график , на котором показать экспериментальные и расчетные значения (см. рис. 4) и сделать выводы по работе.