ЧАСТЬ 8

Случайные процессы. Типы случайных процессов ( процессы с независимыми

однородными приращениями, процессы стационарные в узком и широком смысле).

Ковариационная функция случайного процесса

Пуассоновский процесс (определения и свойства )

Винеровский процесс. Определения. Ковариационная функция. Свойства траекторий

Распределение максимума винеровского процесса

Случайные процессы. Простейшие определения.

Опр.

Замечание.

1. удобно рассматривать T как время.

2. уже рассматривались случайные процессы, в которых роль T

исполняли мн-ва N, [1..n] и др,- последовательности случайных

величин.

- можно рассматривать при фиксированном t как случайную величину,

а при фиксированном как траекторию случайного процесса.

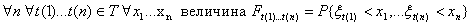Опр.

называется конечномерным распределением

введем обозначения

Опр. Процесс называется процессом с независимыми приращениями,

если

Замечание.

Для таких процессов достаточно знать одномерные распределения.

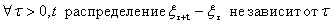Опр. Процесс с независимыми приращениями имеет однородные (стационарные) приращения, если

Тогда A(t)=A(s)+A(t-s)

D(t)=D(s)+D(t-s), а эти равенства приводят к тому, что

A, D - линейные ф-ции

Пример процесса с однородными независимыми приращениями

с независимыми приращениями

если величины Xi - имеют одинаковые распределения, то соотв. процесс

будет процессом с однородными приращениями.

т. о. случайные блуждания на целочисленной оси представляют собой процесс с однородными приращениями.

Опр. Процесс называется стационарным (в узком смысле), если

для них выполняются следующие св-ва:

A(t)=const, D(t)=const, B(t, s)=B(s-t)

Опр. Процесс называется стационарным в широком смысле, если

A(t)=const

B(t, s)=B(s-t),s>t

Замечание

1. можно считать A(t)=0, рассматривая, если необходимо,

2. для стационарных в широком смысле процессов необходимо существование мат. ожидания и второго момента.

Пример стационарных процессов:

стационарный в узком смысле -

если независимы и одинаково распределены

стационарный в широком (но не в узком) смысле -

любая последовательность независимых случайных величин, у

которых распределения разные, а мат. ожидания и дисперсии совпадают.

Пуассоновский процесс

Опр. Процесс с независимыми однородными приращениями называется пуассоновским (с параметром l), если .

Замеч. m=0,1,2,…

Траектории процесса имеют единичные скачки с вероятностью 1 в точках z1+z2+…+zk, где z1, z2 – независимы и имеют экспоненциальное распределение с параметром , т. е. .

Винеровский процесс

Обозн. Винеровский процесс W(t) t³0, W(0)=0.

Опр. Процесс W(t) с независимыми однородными приращениями называется винеровским, если .

Математические характеристики:

1) , т. к. .

2) .

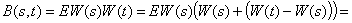
3) (используем, что приращения W(t)-W(s) независимы). Аналогично при . Таким образом получаем .

Свойство траекторий винеровского процесса: они с вероятностью 1 непрерывны, но нигде не дифференцируемы /без док-ва/.

Рассмотрим – нез. одинак. распределенные с. в.: , 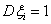. Рассмотрим другую последовательность с. в.: , . Построим ломаную с вершинами . Получим непрерывную случайную (т. к. 2-ая координата случайна) ломаную.

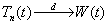при ,.

Принцип инвариантности:

Последовательность ломаных сходится в некотором смысле (по распределению) к винеровскому процессу.

Из принципа инвариантности следует, что можно рассматривать асимптотические соотношения, эквивалентные соотношениям для винеровского процесса. Например: , где . Если найдем распределение функционала от винеровского процесса, то найдем распределение соответствующего функционала от сумм. Более того, достаточно найти предельное распределение функционала для случая, когда исходные величины имеют какое-то простое распределение (например, двухточечное), чтобы найти H(x) и из принципа инвариантности следует, что это же распределение будет предельным и для случая произвольных – нез. одинак. распределенных с. в., у которых , 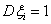. Для рассматриваемого нами функционала используется принцип отражения. Рассмотрим те траектории винеровского процесса , которые за единичное время достигнут уровня выше x. Вероятность такого события .

Рассмотрим значения таких траекторий в единице, т. е. W(1):

1) W(1)>x Þ максимум траектории больше уровня x; W(1)~N(0,1) Þ знаем вероятность .

2) W(1)<x Þ принцип отражения: если , то существует точка M, в которой траектория (непрерывная) впервые достигает уровня x. Т. к. мы рассматриваем нормальное распределение (симметричное) и винеровский процесс имеет независимые приращения, то можно данной 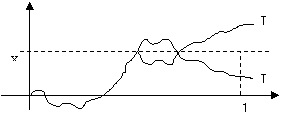траектории сопоставить симметричную (относительно x), начиная с точки M. Множества траекторий I и II имеют одинаковую меру. Поэтому можно получить следующую формулу:, где .