Днепродзержинский государственный технический университет
ОТЧЕТ О ПРАКТИКЕ
На тему:
«РУПОРНЫЕ АНТЕНЫ»
Выполнил студент группы АРТ-00-1д
г. Днепродзержинск
2004 г.
Классификация рупорных антенн
В диапазоне сантиметровых волн широко применяются рупорные антенны. Они используются как отдельные передающие и приемочные антенны в радиолокации, радиорелейной связи, измерительной аппаратуре, а также, как излучатели сложных антенных устройств, в частности зеркальных антенн.
Рупорные антенны являются простыми по конструкции, широкодиапазонные. Они имеют сравнительно низкий уровень бокового излучения (коэффициент усиления достигает 20-25 дБ, ширина диаграммы направленности - 10-20°). Рупорная антенна состоит из отрезка волновода постоянного перереза и рупора, который представляет собой волновод, размеры поперечного перереза которого медленно возрастают в продольном направлении. Длиной рупора R принято называть расстояние от средней точки розкрыва к представленной точке пересечения линий, которые продолжают стенки рупора.
Размеры поперечного перереза избираются таким образом, чтобы обеспечить формирование необходимой структуры поля. При достаточно медленном изменении размеров рупора структура электромагнитного поля в рупоре подобная к структуре поля в питательном волноводе. С ростом апертуры увеличивается коэффициент усиления рупора, а также улучшается согласование рупора с свободным пространством.
Используются два типа прямоугольных рупоров - секториальные и пирамидальные (рис. 1). Секториальные - это рупоры, в которых расширяется только одна пара стенок. В зависимости от того, в какой плоскости происходит распространение, отличают Е- плоскостные (рис. 1,а) и Н-плоскостные (рис. 1,б) секториальные рупоры. Если распространение происходит в обоих плоскостях, то рупор называется пирамидальным (рис. 1,в). Эти рупоры, в свою очередь, разделяют на клинообразные (рис. 1,в) и остроугольные (ребра рупора совпадают в одну точку).
Рупоры круглого перереза обычно расширяются равномерно по всем направлениям (рис. 1,г). Такие рупоры называются коническими.
При анализе направленности рупорных антенн можно считать, что излучение происходит только из поверхности раскрыва рупора. Действительно, основная волна, которая поступает из волновода, дифрагирует на краях вскрыши и приводит электрические тока на внешней поверхности стенок рупора. Однако излучением этих токов можно пренебречь. Причем погрешность будет тем меньше, чем большие размеры раскрыва рупора относительно длины волны.
 |
В секториальных рупорах излучается волна с цилиндрическим фазовым фронтом, а в пирамидальных - с сферическим. При расчетах параметров рупорных антенн можно считать, что их направленность обусловлена размерами поверхности раскрыва и законом распределения амплитуды фазы поля в раскрыве.
Рис. 1. Типы рупорных антенн:
а - Е-плоскостной рупор; б - Н- плоскостной рупор;
в - секториальний рупор; г - конический рупор
Для объяснения принципов работы рупорной антенны рассмотрим ее продольный перерез. Электромагнитная энергия от генератора через отрезок питательного волновода поступает к горловине рупора в виде волны с плоским фронтом. Большая часть энергии проходит сквозь горловину и распространяется вдоль рупора в виде расходящейся волны. Небольшая частица энергии отбивается от горловины и возвращается к генератору. Чем сильнее выраженная неоднородность в точке перехода от волновода к рупору, то есть чем больший угол расклона рупора, тим больший коэффициент отражения. Достигши раскрыва, который есть границей распределения между рупором и свободным пространством, большая часть энергии излучается, но частица энергии отбивается и отправляется в обратном направлении. При больших размерах раскрыва в Н-плоскости коэффициент отражения от него обычно маленький, и этот факт разрешает рассматривать рупор как устройство, которое согласовывает волнововод с свободным пространством.
Согласование можно улучшить, пользуясь так называемыми комбинированными рупорами, поперечный размер которых изменяется сначала в одной плоскости, а потом в другом. При определенным образом отобранных размерах рупора отражения от двух горловин и раскрыва взаимно компенсируются.
Если угол расклона рупора маленький, то структура поля, как и распределение амплитуды поля в раскрыве рупора такой же, как и в питательном волноводе. Однако есть и существенные отличия. Волна в волноводе, который расширяется, является цилиндрической, то есть фазовый фронт волны образовывает часть поверхности цилиндра, ось которого проходит через вершину рупора. Обычно в прямоугольном волноводе возбуждается волна типа Н10.
Структура поля в Н-плоскостном рупоре, который питается с помощью прямоугольного волновода, показанная на рис. 2,а. Поле в рупоре отображается через цилиндрическую функцию, которая имеет вид
(1)
где В - величина постоянной, что характеризует амплитуду поля;
р - расстояние от вершины рупора к точке М, где определяется поле.
 |
Уменьшение амплитуды по закону
является характерным для цилиндрической волны. Множитель соs(πΦ/2Φ0) обеспечивает равенство нулю касательной составной электрического поля возле узких стенок рупора (при Ф=±Ф0). Множитель exp(-jkp) показывает, что волна распространяется вдоль рупора с фазовой скоростью, которая практически равняется скорости света в вакууме. Потому что размер широкой стенки рупора увеличивается, в Н-секториальном рупоре фазовая скорость с ростом р уменьшается от фазовой скорости в волноводе к скорости света, которой практически равняется уже на сравнительно небольшом расстоянии от горловины рупора (при ар >> 
).
Рис. 2. Распределение электромагнитного поля:
а - Н-секториальные рупоры; б - Е-секториальные рупоры
Для любой точки А у раскрива рупора р =
, где R — длина рупора. Подставим это значение в (1) и учтем, что при небольших углах расклона рупора (2Ф0 < 60˚ ) можно предполагать такие приближения:
Определяем выражение для поля в раскрыве Н-плоскостного рупора в виде
где Е0 - амплитуда поля в центре раскрива, фазовый множитель exp(-jkх2/2R) опускаем.
В плоскости Е распределение амплитуды поля равномерное, а в плоскости H, если проводить отсчет от центра, амплитуда распределяется по закону соs(πx/ар). При таком распределении диаграммы направленности в плоскостях Е и Н при отсутствии фазовых искажений определяются в соответствии с формулами
(2)
где U = kLsinΘ/2; Θ - угол между нормалью к поверхности раскрыва и направлением к точке наблюдения; L - линейный размер раскрыва; k = 2π/λ - волновое число; λ — длина волны в свободном пространстве.
На рис. 2,б изображена структура поля в секториальном Е-плоскостном рупоре. И в этом случае волна является цилиндрической, но потому что размер рупора в плоскости магнитного вектора не изменяется, фазовая скорость остается постоянной. Она равняется фазовой скорости волновода. Приближенное выражение для амплитудно-фазового распределения поля в раскрыве Е-плоскостного секториального рупора имеет вид
где kb = 2π/Λ ; Λ- длина волны в рупоре.
Ведь в Н-плоскости изменяется только амплитуда (по косинусоидальному закону), а в Е-плоскости только фаза (по квадратичному закону).
На рис. 3 изображенные диаграммы направленности, которые было рассчитано по формулам (2), что отвечают равномерному (сплошная линия) и косинусоидальному (пунктирная линия) распределению амплитуды поля. Из этого рисунка видим, что спад амплитуды на краях приводит к расширению главного лепестка диаграммы направленности при значительном снижении уровня бокового излучения. При косинусоидальном распределении амплитуды уровень максимального бокового лепестка составляет около 7 % (~ -23 дБ), а при равномерном распределении - 22 % (~ -13 дБ).
 |
Из этого явствует, что если рупор имеет квадратный раскрыв (ар - bр), то в плоскости Е диаграмма направленности будет уже, чем в плоскости Н, и уровень боковых лепестков в плоскости Е будет большей, чем в плоскости Н.
Рис. 3. Диаграммы направленности секториальних рупоров.
При рассмотрении влияния амплитудного распределения поля в раскрыве антенны на его направленность допускалось, что поверхность раскрыва рупора была возбуждена синфазно. Однако волновой фронт в рупоре имеет форму цилиндрической или сферической поверхности, поэтому фаза поля на краях рупора будет другой, чем в центре. Возникают так называемые "фазовые погрешности". То есть для обозначения направленности рупорной антенны следует рассматривать излучать из раскрыва как поле, которое неравномерно не только по амплитуде, но и по фазе.
Максимальное отклонение фазы напряженности поля для секториальных рупоров будет на краях раскрыва. Оно будет определяться выражением
(3)
где L - линейный размер раскрыва рупора (для плоскости Е - L = bp, для плоскости Н - L = ар); λp - длина волны в рупоре; R - длина рупора.
Максимальное отклонение фазы напряженности поля для пирамидальных рупоров будет в углах раскрива рупора. Оно будет определяться таким образом:
(4)
где ар и bр - размеры раскрыва рупора; λp - длина волны в рупоре; RH и RE - длина рупора соответственно в Е- и Н-плоскостях.
При увеличении раскрыва рупора в плоскости Н фазовая скорость электромагнитной волны приближается к скорости света в свободном пространстве. Поэтому в первом приближении можно предположить, что фазовая скорость в раскрыве Н-секториальных и пирамидальных рупоров равняется скорости света, и в формулах (3)-(4) вместо λp подставить длину волны в свободном пространстве λ. Для Е-секториальных рупоров можно предположить, что λp равняется длине волны в питательном волноводе. Как видим из формул (3) и (4), распределение фазы напряженности поля в раскрыве рупора приближенно описывается квадратичным законом.
Нарушение синфазности поверхности излучения приводит к искажению диаграммы направленности антенны. Искажения, которые обусловленные квадратичностью фазового распределения, вызывают расширение главного лепестка диаграммы направленности, увеличение уровня боковых лепестков и исчезновение нулевых провалов между лепестками. Причем величина искажения диаграммы направленности зависит от амплитудного распределения в раскрыве антенны.
Коэффициент направленного действия реальной апертурной антенны можно найти по формуле:
где S - геометрическая поверхность антенны; Кon - коэффициент использования поверхности.
Величина коэффициента использования поверхности определяется неравномерностью распределения амплитуды и фазовым искажением на поверхности излучения. Для реальных рупорных антенн Кon находится в границах - 0,5-0,8.
При увеличении раскрыва при неизменной длине рупора КСД сначала возрастает, а потом уменьшается. Величина максимума увеличивается при возрастании длины рупора. Это обусловленно тем, что КСД пропорционален площади поверхности раскрыва S и коэффициенту ее использования Кon. При возрастании S КСД увеличивается, одновременно возрастают фазовые искажения коэффициента использования поверхности. Максимуму КСД отвечают оптимальные условия, если поверхность S достаточно большая и величина коэффициента Кon не очень маленькая.
Анализ показывает, что этот факт характерный для Е-секториальных рупоров, если выполняется равенство:
(5)
тогда угловая ширина диаграммы направленности на уровне 0,5 в Н- и Е-плоскостях (у рад.) равняется:
(6)
Аналогично, для Н-секториальных рупоров оптимальные условия наблюдаются при
а ширина главного лепестка в Н- и Е-плоскостях в таком случае будет
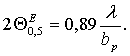(7)
КСД оптимального секториального рупора определяется выражением
где Sp - площадь раскрыва рупора; Кon ~ 0,64.
На основе формул (3), (6) и (7) можно показать, что максимальные фазовые искажения в раскрыве рупора при оптимальных условиях в Е-плоскости равняются:
а в Н-плоскости:
Если оставлять постоянной площадь раскрыва S и неограниченное увеличивать длину рупора R, то коэффициент использования поверхности Кon будет возрастать, и в случае, если R → ∞(?? = 0), будет равняться
Для оптимальных рупоров
Коэффициент усиления антенны равняется
где ηΛ - коэффициент полезного действия антенны. Потому что потери в рупорных антеннах маленькие, обычно предполагают ηΛ = 1.
Размеры оптимального пирамидального клинообразного рупора можно рассчитать с помощью формул для Е- и Н-секториальных рупоров (5) и (8), а оптимального остроугольного определить из выражений
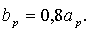
Ширяла главного лепестка диаграммы направленности оптимального пирамидального рупора в Н- и Е-плоскостях на равные 0,5 (у рад.) будет определяться формулами
Коэффициент направленного действия пирамидального рупора можно приближенно определить так:
или через КСД секториальных рупоров (DЕ и DН) с размерами, как и для пирамидального рупора в соответствующих плоскостях:
Ширина ДС пирамидального рупора (в градусах) будет определяться в соответствии с формулами
(8)
